Formula dan persamaan probabilitas bersyarat, sifat, contoh

Itu probabilitas bersyarat Itu adalah kemungkinan terjadinya suatu peristiwa tertentu, karena yang lain terjadi sebagai suatu kondisi. Informasi tambahan ini dapat memodifikasi (atau mungkin tidak) persepsi bahwa sesuatu akan terjadi.

Misalnya, kita dapat bertanya pada diri sendiri: “Berapa probabilitas hujan hari ini, karena dua hari yang lalu tidak hujan?". Peristiwa yang ingin kami ketahui probabilitasnya adalah hujan hari ini, dan informasi tambahan yang akan mengkondisikan jawabannya adalah bahwa "dua hari yang lalu tidak hujan".

Gambar 1. Probabilitas hujan hari ini sejak hujan kemarin juga merupakan contoh probabilitas bersyarat. Sumber: Pixabay.

Jadilah a Ruang probabilistik terdiri dari Ω (ruang sampel), ℬ (peristiwa acak) dan p (probabilitas setiap peristiwa), ditambah peristiwa A dan B milik ℬ.

Probabilitas yang dikondisikan yang terjadi pada, karena B, yang dilambangkan sebagai P (A│B), didefinisikan dengan cara ini:

P (a│b) = p (a∩b) / p (b) = p (a dan b) / p (b)

Di mana: P (A) adalah probabilitas kemunculan A, P (b) adalah probabilitas peristiwa B dan berbeda dari 0, dan p (a∩b) adalah probabilitas persimpangan antara A dan B, yaitu ,, probabilitas bahwa kedua peristiwa terjadi (probabilitas bersama).

Ini adalah ekspresi untuk teorema Bayes yang diterapkan pada dua peristiwa, yang diusulkan pada 1763 oleh teolog Inggris dan ahli matematika Thomas Bayes.

[TOC]

Properti

-Semua probabilitas bersyarat adalah antara 0 dan 1:

0 ≤ p (a│b) ≤ 1

-Probabilitas bahwa peristiwa tersebut akan terjadi, karena peristiwa ini terjadi, jelas 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Jika dua peristiwa eksklusif, yaitu, peristiwa yang tidak dapat terjadi secara bersamaan, maka probabilitas bersyarat bahwa salah satunya terjadi adalah 0, karena persimpangan batal:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Jika B adalah subset dari A, maka probabilitas bersyarat juga 1:

Dapat melayani Anda: Toroid atau Toro Dona

P (b│a) = p (a∩b) / p (a) = 1

Penting

P (A│B) Umumnya tidak sama dengan P (B│A), oleh karena itu Anda harus berhati -hati untuk tidak bertukar peristiwa saat menemukan probabilitas bersyarat.

Aturan umum perkalian

Sering kali Anda ingin menemukan probabilitas sendi p (a∩b), bukan probabilitas bersyarat. Jadi, melalui teorema berikut yang Anda miliki:

P (a∩b) = p (a dan b) = p (a│b). P (b)

Teorema dapat diperpanjang untuk tiga acara A, B dan C:

P (a∩b∩c) = p (a dan b dan c) = p (a) · p (b│a) · p (c│a∩b)

Dan juga untuk beberapa acara, seperti₁, KE₂, KE₃ Dan lebih dari itu dapat dinyatakan sebagai berikut:

P (a₁∩ a₂ ∩ a₃… ∩ A_N) = P (a₁) . P (a₂│A₁). P (a₃│A₁∩ a₂) ... p (a_N│A₁∩ a₂∩ ... a_N-1)

Ketika itu adalah kasus peristiwa yang terjadi secara berurutan dan melalui tahap yang berbeda, lebih mudah untuk mengatur data dalam diagram atau tabel. Ini memfasilitasi memvisualisasikan opsi untuk mencapai probabilitas yang diminta.

Contohnya adalah diagram pohon dan tabel kontingensi. Dari salah satu dari mereka, Anda dapat membangun yang lain.

Contoh probabilitas bersyarat

Mari kita lihat beberapa situasi di mana probabilitas suatu peristiwa diubah oleh terjadinya orang lain:

- Contoh 1

Di toko manis dua jenis kue terjual: stroberi dan cokelat. Saat mendaftarkan preferensi 50 klien dari kedua jenis kelamin, nilai -nilai berikut ditentukan:

-27 wanita, yang 11 lebih suka stroberi dan 16 kue cokelat.

-23 pria: 15 cokelat dan 8 stroberi.

Probabilitas bahwa pelanggan memilih kue cokelat dapat ditentukan dengan menerapkan aturan Laplace, yang menurutnya probabilitas peristiwa apa pun adalah:

P = jumlah acara yang menguntungkan/jumlah total acara

Dalam hal ini, dari 50 klien, total 31 lebih suka cokelat, sehingga probabilitasnya adalah p = 31/50 = 0.62. Yaitu, 62% pelanggan lebih suka kue cokelat.

Dapat melayani Anda: persamaan polinomial

Tapi apakah akan berbeda jika klien adalah seorang wanita? Ini adalah kasus probabilitas bersyarat.

Tabel kontingensi

Melalui tabel kontingensi seperti ini, total mudah divisualisasikan:

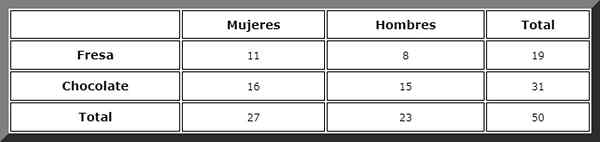
Kemudian kasus yang menguntungkan diamati dan aturan Laplace diterapkan, tetapi sebelum kita mendefinisikan peristiwa:

-B adalah acara "Klien Wanita".

-A adalah acara "lebih suka kue cokelat" menjadi seorang wanita.

Kami pergi ke kolom berlabel "wanita" dan di sana kami melihat bahwa totalnya 27.

Maka kasus yang menguntungkan dicari di baris "cokelat". Ada 16 peristiwa ini, oleh karena itu probabilitas yang dicari adalah secara langsung:

P (a│b) = 16/27 = 0.5924

A 59.24 % wanita wanita lebih suka kue cokelat.

Nilai ini bertepatan ketika kita kontras dengan definisi probabilitas bersyarat yang diberikan pada awalnya:

P (a│b) = p (a∩b) / p (b)

Kami memastikan diri kami melalui aturan Laplace dan nilai -nilai tabel:

P (b) = 27/50

P (a dan b) = 16/50

Di mana p (a dan b) adalah probabilitas bahwa klien lebih memilih cokelat dan seorang wanita. Sekarang nilainya diganti:

P (a│b) = p (a dan b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

Dan terbukti bahwa hasilnya sama.

- Contoh 2

Dalam contoh ini aturan multiplikasi berlaku. Misalkan dalam pameran toko ada celana dalam tiga ukuran: kecil, sedang dan besar.

Dalam banyak hal dengan total 24 celana, di mana ada 8 dari setiap ukuran dan semuanya dicampur. Apa yang akan menjadi probabilitas mengekstraksi dua dari mereka dan keduanya kecil?

Jelas bahwa probabilitas mengekstraksi celana kecil dalam upaya pertama adalah 8/24 = 1/3. Sekarang, ekstraksi kedua dikondisikan ke acara pertama, karena ketika Anda mengeluarkan celana, tidak ada lagi 24, tetapi 23. Dan jika celana kecil dilepas, ada 7 bukan 8.

Dapat melayani Anda: Prinsip Multiplikasi: Teknik dan Contoh Penghitungan

Acara A adalah untuk mengeluarkan celana kecil, setelah mengambil satu lagi dalam upaya pertama. Dan peristiwa B adalah celana kecil ke yang pertama. Karena itu:

P (b) = 1/3; P (a│b) = 7/24

Akhirnya, melalui aturan multiplikasi:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Olahraga diselesaikan

Dalam studi ketepatan waktu pada penerbangan udara komersial, data berikut tersedia:

-P (b) = 0.83, adalah probabilitas yang diambil oleh pesawat terbang untuk mengambil waktu tepat waktu.

-P (a) = 0.81, adalah probabilitas pendaratan tepat waktu.

-P (b∩a) = 0.78 Ini adalah probabilitas bahwa penerbangan akan tiba tepat waktu mengambil waktu tepat waktu.

Itu diminta untuk menghitung:

a) Berapa probabilitas bahwa pesawat mendarat segera karena lepas landas tepat waktu?

b) Probabilitas di atas sama dengan probabilitas bahwa ia telah keluar tepat waktu jika Anda berhasil mendarat segera?

c) dan akhirnya: Berapa probabilitas bahwa itu akan datang tepat waktu karena tidak keluar tepat waktu?

Gambar 2. Ketepatan waktu pada penerbangan komersial adalah penting, karena penundaan menghasilkan kerugian jutawan. Sumber: Pixabay.

Solusi untuk

Untuk menjawab pertanyaan, definisi probabilitas bersyarat digunakan:

P (a│b) = p (a∩b) / p (b) = p (a dan b) / p (b) = 0.78/0.83 = 0.9398

Solusi b

Dalam hal ini, acara dipertukarkan dalam definisi:

P (b│a) = p (a∩b) / p (a) = p (a dan b) / p (a) = 0.78/0.81 = 0.9630

Perhatikan bahwa probabilitas ini sedikit berbeda dari yang sebelumnya, seperti yang kami sebutkan sebelumnya.

Solusi c

Probabilitas tidak tepat waktu adalah 1 - p (b) = 1 - 0,83 = 0.17, kami akan menyebutnya p (b^C), Karena itu adalah acara pelengkap untuk mengambil waktu tepat waktu. Probabilitas bersyarat yang dicari adalah:

P (A│B^C) = P (a∩b^C) / P (b^C) = P (a dan b^C)/P (b^C)

Di samping itu:

P (A∩B^C) = P (waktu pendaratan) - p (waktu pendaratan dan lepas landas) = ​​0.81-0.78 = 0.03

Dalam hal ini, probabilitas yang dicari adalah:

P (A│B^C) = 0.03/0.17 = 0.1765

Referensi

1. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Seri Schaum: Probabilitas. Bukit McGraw.
4. Obregón, i. 1989.Teori probabilitas. Limusa editorial.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.
6. Wikipedia. Probabilitas yang dikondisikan. Pulih dari: is.Wikipedia.org.