Probabilitas Teoritis Cara mengeluarkannya, contoh, latihan

Itu Probabilitas teoritis (atau dari Laplace) bahwa suatu peristiwa terjadi yang dimiliki oleh ruang sampel S, di mana semua peristiwa memiliki probabilitas kejadian yang sama, itu didefinisikan dalam notasi matematika seperti: p (e) = n (e) / n ( S)

Di mana p (e) adalah probabilitas, diberikan sebagai rasio antara jumlah total hasil yang mungkin dari peristiwa E, yang kami sebut n (e), dibagi dengan jumlah total n (s) hasil yang mungkin dalam ruang sampel s.

Gambar 1. Pada peluncuran dadu enam sisi, probabilitas teoretis bahwa wajah dengan tiga titik berada di atas adalah ⅙. Sumber: Pixabay.

Probabilitas teoritis adalah bilangan real antara 0 dan 1, tetapi sering dinyatakan dalam bentuk persentase, dalam hal ini probabilitas akan menjadi nilai antara 0% dan 100%.

Menghitung probabilitas terjadinya suatu peristiwa sangat penting di banyak bidang, seperti aktivitas pasar saham, perusahaan asuransi, perjudian dan banyak lagi.

[TOC]

Bagaimana mendapatkan probabilitas teoretis?

Kasus ilustratif adalah kasus rifas atau lotere. Asumsikan itu 1.000 Tiket untuk Rifar A Smartphone. Saat undian dilakukan secara acak, salah satu tiket memiliki peluang yang sama untuk menjadi pemenang. 

Untuk menemukan probabilitas bahwa seseorang yang membeli tiket dengan nomor 81 menjadi pemenang, perhitungan berikut Probabilitas teoritis:

P (1) = 1/1.000 = 0,001 = 0,1%

Hasil sebelumnya ditafsirkan sebagai berikut: Jika undian diulangi secara tak terbatas, setiap 1.000 kali tiket 81 akan dipilih, rata -rata, sekali.

Jika karena alasan apa pun seseorang memperoleh semua tiket, pasti dia akan memenangkan hadiah. Probabilitas memenangkan hadiah jika Anda memiliki semua tiket yang dihitung sebagai berikut:

Itu dapat melayani Anda: perimeter lingkaran: cara mengeluarkannya dan formula, latihan terpecahkan

P (1.000) = 1.000/1.000 = 1 = 100%.

Artinya, probabilitas apa 1 atau 100% berarti bahwa benar -benar yakin bahwa hasil ini akan terjadi.

Jika seseorang memiliki 500 tiket kemungkinan menang atau kalah adalah sama. Probabilitas teoritis untuk memenangkan hadiah dalam kasus ini dihitung sebagai berikut:

P (500) = 500/1.000 = ½ = 0,5 = 50%.

Dia yang tidak membeli tiket apa pun tidak memiliki peluang untuk menang dan probabilitas teoretisnya ditentukan seperti ini:

 P (0) = 0 /1.000 = 0 = 0%

Contoh

Contoh 1

Anda memiliki mata uang dengan mahal di satu sisi dan tameng atau segel di yang lain. Saat mata uang diluncurkan, berapa probabilitas teoretis untuk menjadi mahal?

P (mahal) = n (mahal) / N ( wajah + perisai ) = ½ = 0,5 = 50%

Hasilnya ditafsirkan sebagai berikut: Jika sejumlah besar rilis dibuat, rata -rata di setiap 2 nada yang akan dihadapi salah satu dari mereka.

Dalam istilah persentase, interpretasi hasilnya adalah bahwa membuat sejumlah besar peluncuran, rata -rata setiap 100 dari mereka 50 akan menghasilkan mahal.

Contoh 2

Di dalam kotak ada 3 kelereng biru, 2 kelereng merah dan 1 hijau. Berapa probabilitas teoretis bahwa saat Anda mendapatkan marmer dari kotak ini merah?

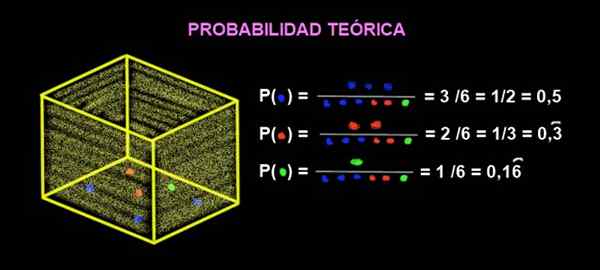Gambar 2. Probabilitas ekstraksi kelereng warna. Sumber: f. Zapata.

Probabilitas yang menjadi merah adalah:

P (merah) = jumlah kasus yang menguntungkan / jumlah kasus yang mungkin terjadi

Artinya:

P (merah) = jumlah kelereng merah / jumlah total kelereng

Akhirnya, probabilitas marmer merah adalah:

P (merah) = 2/6 = ⅓ = 0,3333 = 33,33%

Sementara probabilitas bahwa dengan mengekstraksi marmer hijau adalah:

P (hijau) = ⅙ = 0,1666 = 16,66%

Akhirnya, probabilitas teoritis untuk mendapatkan dalam ekstraksi buta marmer biru adalah: 

P (biru) = 3/6 = ½ = 0,5 = 50%

Itu dapat melayani Anda: sifat radikal

Yaitu, dari setiap 2 upaya hasilnya akan berwarna biru di salah satu dari mereka dan warna lain dalam upaya lain, di bawah premis bahwa marmer yang diekstraksi diisi ulang dan bahwa jumlah uji coba sangat, sangat besar.

Latihan

Latihan 1

Tentukan probabilitas bahwa saat meluncurkan dadu nilai diperoleh kurang dari atau sama dengan 4.

Larutan

Untuk menghitung probabilitas bahwa peristiwa ini terjadi, definisi probabilitas teoritis akan berlaku:

P (≤4) = jumlah kasus yang menguntungkan / jumlah kasus yang mungkin terjadi

P (≤5) = 5/6 = = 83,33%

Latihan 2

Temukan probabilitas bahwa dalam dua nada berturut -turut dari dadu enam -sidah normal, 2 kali 2 kali.

Larutan

Untuk menanggapi latihan ini, lebih mudah untuk membuat gambar untuk menunjukkan semua kemungkinan. Gambar pertama menunjukkan hasil dadu pertama dan yang kedua hasil yang lain.

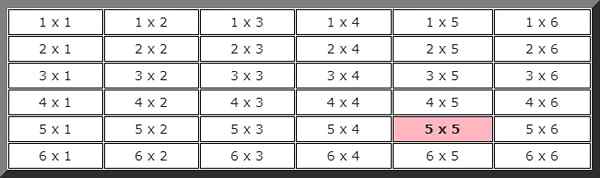
Untuk menghitung probabilitas teoretis, kita perlu mengetahui jumlah total kasus yang mungkin, dalam hal ini seperti yang dapat dilihat dari tabel sebelumnya, ada 36 kemungkinan.

Juga mengamati lukisan itu mengikuti bahwa jumlah kasus yang menguntungkan untuk peristiwa yang dalam dua rilis berturut -turut datang 5 hanya 1, disorot dengan warna, oleh karena itu probabilitas bahwa peristiwa ini akan terjadi adalah:

P (5 x 5) = 1/33.

Hasil ini juga dapat dicapai dengan menggunakan salah satu sifat probabilitas teoritis, yang menyatakan bahwa probabilitas gabungan dari dua peristiwa independen adalah produk dari probabilitas masing -masing.

Dalam hal ini probabilitas bahwa dalam rilis pertama 5 adalah ⅙. Peluncuran kedua sepenuhnya independen dari yang pertama, oleh karena itu probabilitas bahwa 5 di yang kedua juga ⅙. Jadi probabilitas gabungannya adalah:

Dapat melayani Anda: turunan parsial: properti, perhitungan, latihan

P (5 × 5) = p (5) p (5) = (1/6) (1/6) = 1/36.

Latihan 3

Temukan probabilitas bahwa angka kurang dari 2 keluar dalam peluncuran pertama dan pada yang kedua angka yang lebih besar dari 2 keluar. 

Larutan

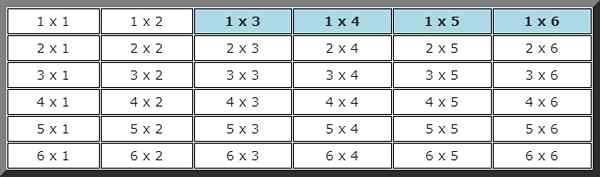
Sekali lagi Anda harus membangun tabel acara yang mungkin, di mana di mana peluncuran pertama kurang dari 2 dan di kedua lebih tinggi dari 2 digarisbawahi.

Secara total ada 4 kemungkinan dari total 36. Dengan kata lain, probabilitas acara ini adalah:

P (2) = 4/36 = 1/9 = 0.1111 = 11.11%

Menggunakan teorema probabilitas yang menyatakan:

Probabilitas terjadinya dua peristiwa independen sama dengan produk probabilitas individu.

Itu diperoleh hasil yang identik:

P (2) = (1/6) (4/6) = 4/36 = 0.1111 = 11.11%

Nilai yang diperoleh dengan prosedur ini bertepatan dengan hasil sebelumnya, melalui definisi probabilitas teoritis atau klasik.

Latihan 4

Berapa probabilitas bahwa dengan meluncurkan dua mengingat jumlah nilainya adalah 7.

Larutan

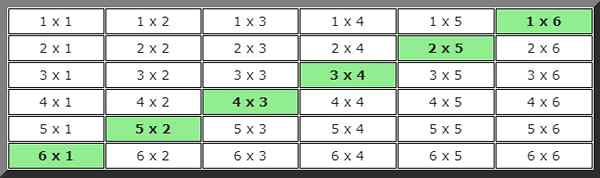
Untuk menemukan solusi dalam kasus ini, gambaran kemungkinan telah dikembangkan di mana kasus -kasus yang memenuhi kondisi nilai -nilai 7 telah ditunjukkan dalam warna.

Melihat meja, 6 kemungkinan kasus dapat dihitung, jadi probabilitasnya adalah:

P (R & D II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%

Referensi

1. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Lipschutz, s. 1991. Seri Schaum: Probabilitas. Bukit McGraw.
4. Obregón, i. 1989.Teori probabilitas. Limusa editorial.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.