Produk yang luar biasa

Produk apa yang terkenal?

Produk penting adalah operasi aljabar, di mana multiplikasi polinomial diungkapkan, yang tidak perlu diselesaikan secara tradisional, tetapi dengan bantuan aturan tertentu, hasil yang sama dapat ditemukan.

Polinomial dikalikan apakah, oleh karena itu dimungkinkan bahwa mereka memiliki banyak istilah dan variabel. Untuk membuat prosesnya singkat, aturan produk terkenal digunakan, yang memungkinkan multiplikasi tanpa harus menggunakan istilah untuk jangka waktu.

Produk dan contoh penting

Setiap produk yang luar biasa adalah formula yang dihasilkan dari faktorisasi, terdiri dari polinomial dari beberapa istilah seperti binomial atau trinomial, yang disebut faktor.

Faktor -faktor tersebut adalah dasar dari suatu kekuatan dan memiliki eksponen. Saat faktor bertambah, eksponen harus ditambahkan.

Ada beberapa formula produk penting, beberapa lebih banyak digunakan daripada yang lain, tergantung pada polinomial, dan sebagai berikut:

Binomial persegi

Ini adalah penggandaan binomial dengan sendirinya, dinyatakan dalam bentuk kekuatan, di mana istilah ditambahkan atau dikurangi:

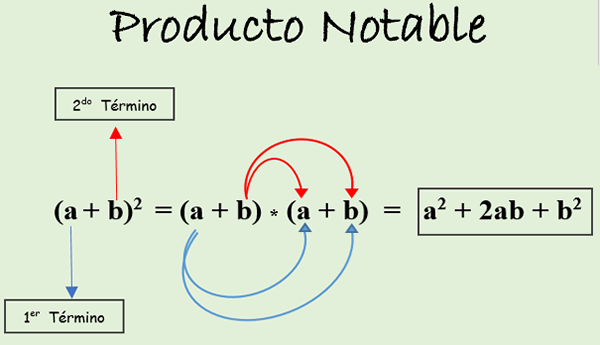
ke. Binomial Jumlah Square: Itu sama dengan kuadrat dari istilah pertama, ditambah dua kali lipat produk dari istilah, ditambah kuadrat dari istilah kedua. Itu dinyatakan sebagai berikut:

(A + B)² = (a + b) _* (A + B).

Dalam gambar berikut Anda dapat melihat bagaimana produk dikembangkan sesuai dengan aturan yang disebutkan di atas. Hasilnya disebut trinomial dari kotak yang sempurna.

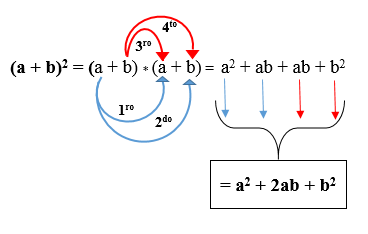
Contoh 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Contoh 2

(4a + 2b) = (4a)² + 2 (ke -4 _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

B. Binomial dari pengurangan persegi: Aturan binomial yang sama dari suatu jumlah diterapkan, hanya bahwa dalam hal ini istilah kedua negatif. Formulanya adalah sebagai berikut:

(A - b)² = [(a) + (- b)]²

Dapat melayani Anda: analogi numerik: jenis, aplikasi dan latihan

(A - b)² = a² +2nd _* (-b) + (-b)²

(A - b)²   = a² - 2ab + b².

Contoh 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Produk Binomials Konjugasi

Dua binomial terkonjugasi ketika ketentuan kedua masing -masing memiliki tanda yang berbeda, yaitu, yang pertama adalah positif dan negatif kedua atau sebaliknya. Itu diselesaikan dengan menaikkan setiap monomial kuadrat dan dikurangi. Formulanya adalah sebagai berikut:

(A + B) _* (A - b)

Pada gambar berikut, produk dari dua binomial terkonjugasi dikembangkan, di mana diamati bahwa hasilnya adalah perbedaan kotak kotak.

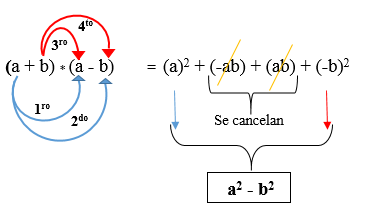
Contoh 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 ab) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produk dari dua binomial dengan istilah umum

Ini adalah salah satu produk penting yang paling kompleks dan sedikit digunakan karena merupakan penggandaan dua binomial yang memiliki istilah umum. Aturan menunjukkan yang berikut:

• Kuadrat dari istilah umum.
• Ditambah jumlah istilah yang tidak umum dan kemudian melipatgandakannya dengan istilah umum.
• Ditambah jumlah penggandaan istilah yang tidak umum.

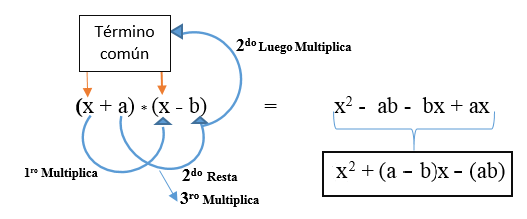
Itu diwakili dalam rumus: (x + a) _* (x + b) dan dikembangkan seperti yang ditunjukkan pada gambar. Hasilnya adalah trinomial persegi yang tidak sempurna.

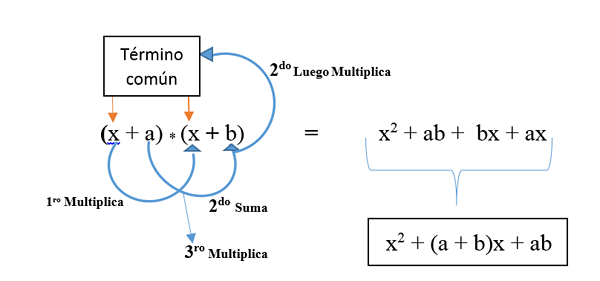Contoh 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Ada kemungkinan bahwa istilah kedua (istilah yang berbeda) negatif dan formulanya adalah sebagai berikut: (x + a) _* (x - b).

Contoh 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Ini juga bisa menjadi kasus bahwa kedua istilah yang berbeda itu negatif. Formula Anda akan menjadi: (x - a) _* (x - b).

Dapat melayani Anda: teorema lamy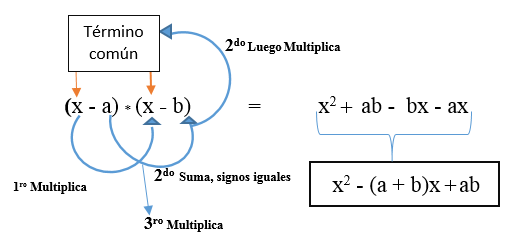

Contoh 3

(3b - 6) _* (3b - 5) = (3b _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3b - 6) _* (3b - 5) = 9b² + (-sebelas) _* (3b) + (30)

(3b - 6) _* (3b - 5) = 9b² - 33b + 30.

Polinomial persegi

Dalam hal ini ada lebih dari dua istilah dan untuk mengembangkannya, masing -masing dipotong dan ditambahkan bersama dengan dua kali perkalian satu istilah dengan yang lain; Formulanya adalah: (A + B + C)² Dan hasil operasi adalah kuadrat trinomial.

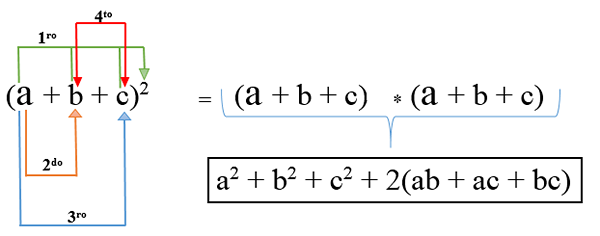
Contoh 1

(3x + 2y + 4z)² = (3x)² + (2 dan)² + (4z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16z² + 12xy + 24xz + 16yz.

Binomial Kubus

Ini adalah produk penting yang kompleks. Untuk mengembangkannya, binomial dikalikan dengan kuadratnya, sebagai berikut:

ke. Untuk binomial ke kubus jumlah:

• Istilah pertama kubus, ditambah triple kuadrat dari istilah pertama dengan yang kedua.
• Ditambah tiga kali lipat istilah pertama, dengan kuadrat kedua.
• Ditambah kubus dari masa jabatan kedua.

(A + B)³ = (a + b) _* (A + B)²

(A + B)³ = (a + b) _* (ke² + 2ab + b²)

(A + B)³ = a³ + 2nd²B + AB² + ba² + 2ab² + B³

(A + B)³ = a³ + 3²B + 3AB² + B³.

Contoh 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

B. Untuk binomial ke kubus pengurangan:

• Kubus dari istilah pertama, kecuali tiga kuadrat dari istilah pertama dengan yang kedua.
• Ditambah tiga kali lipat istilah pertama, dengan kuadrat kedua.
• Kurang kubus dari masa jabatan kedua.

(A - b)³ = (a - b) _* (A - b)²

(A - b)³ = (a - b) _* (ke² - 2ab + b²)

(A - b)³ = a³ - 2nd²B + AB² - ba² + 2ab² - B³

(A - b)³ = ke³ - 3²B + 3AB² - B³.

Contoh 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Dapat melayani Anda: data yang tidak dikelompokkan: contoh dan olahraga diselesaikan

(B - 5)³ = b³ - 15b² +75B - 125.

Kubus Trinomial

Itu berkembang mengalikannya dengan alun -alunnya. Ini adalah produk luar biasa yang sangat luas karena ada 3 istilah yang diangkat ke kubus, ditambah tiga kali lipat dari setiap istilah yang direkrut, dikalikan dengan masing -masing istilah, ditambah enam kali produk dari tiga istilah tersebut. Terlihat dalam bentuk yang lebih baik:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (ke² + B² + C² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + B³ + C³ + 3²B + 3AB² + 3²C + 3AC² + 3b²C + 3BC² + 6abc.

Contoh 1

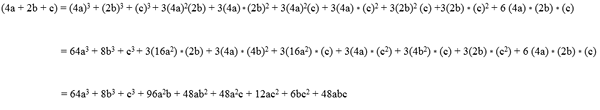
Menyelesaikan latihan produk terkenal

Latihan 1

Kembangkan binomial berikut ke kubus: (4x - 6)³.

Larutan

Mengingat bahwa binomial ke kubus sama dengan istilah pertama yang diangkat ke kubus, kecuali triple dari kuadrat dari istilah pertama dengan yang kedua; ditambah tiga kali lipat istilah pertama, dengan kuadrat kedua, kecuali kubus dari istilah kedua.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Latihan 2

Kembangkan binomial berikut: (x + 3) (x + 8).

Larutan

Anda memiliki binomial di mana ada istilah umum, yaitu x dan istilah kedua positif. Untuk mengembangkannya, hanya istilah umum yang harus ditingkatkan, ditambah jumlah istilah yang tidak umum (3 dan 8) dan kemudian melipatgandakannya dengan istilah umum, ditambah jumlah penggandaan istilah yang tidak umum.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Referensi

1. Malaikat, a. R. (2007). Aljabar Dasar. Pendidikan Pearson,.
2. Arthur Goodman, L. H. ( seribu sembilan ratus sembilan puluh enam). Aljabar dan trigonometri dengan geometri analitik. Pendidikan Pearson.
3. Das, s. (S.F.). Matematika plus 8. Britania Raya: Sagar Ratna.
4. Jerome e. Kaufmann, k. L. (2011). Aljabar Dasar dan Menengah: Pendekatan Gabungan. Florida: Pembelajaran Cengage.
5. Pérez, c. D. (2010). Pendidikan Pearson.