Metode dan latihan pemrograman non -linier

Itu Pemrograman non -linier Ini adalah proses mengoptimalkan fungsi yang tergantung pada beberapa variabel independen, yang pada gilirannya tunduk pada pembatasan.

Jika satu atau lebih dari pembatasan, atau jika fungsi untuk memaksimalkan atau meminimalkan (dipanggil Fungsi objektif), tidak dinyatakan sebagai kombinasi linier dari variabel, jadi ada masalah pemrograman non -linear.

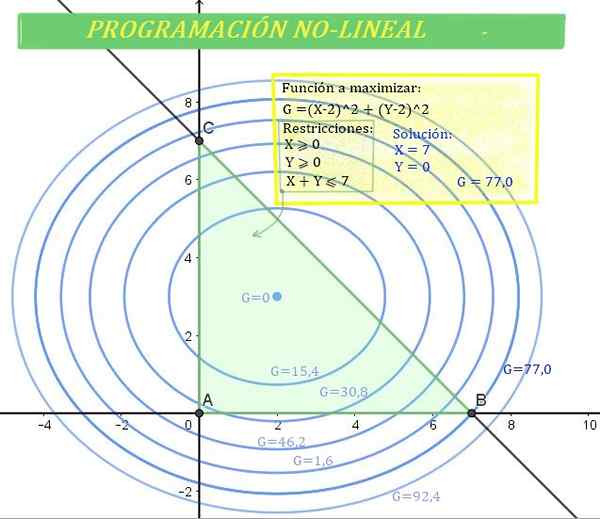
Gambar 1. Masalah Pemrograman Non -Linear (NLP). di mana g adalah fungsi (non-linear) untuk mengoptimalkan di wilayah hijau, ditentukan oleh pembatasan. Sumber: f. Zapata.

Dan oleh karena itu prosedur dan metode pemrograman linier tidak dapat digunakan.

Misalnya, metode yang diketahui dengan baik tidak dapat digunakan Simpleks, yang hanya berlaku ketika fungsi dan batasan objektif adalah kombinasi linier dari variabel masalah.

[TOC]

Metode pemrograman linier

Untuk pemrograman non-linear, metode utama yang akan digunakan adalah: 

1.- Metode grafis.

2.- Pengganda Lagrange untuk menjelajahi perbatasan wilayah solusi.

3.- Perhitungan gradien untuk menjelajahi ujung fungsi objektif.

4.- Metode langkah menurun, untuk menemukan titik nol gradien.

5.- Metode Modifikasi Pengganda Lagrange (dengan kondisi Karush-Kuhn-Tucker).

Contoh solusi dengan metode grafik

Contoh solusi dengan metode grafis adalah apa yang dapat dilihat pada Gambar 2:

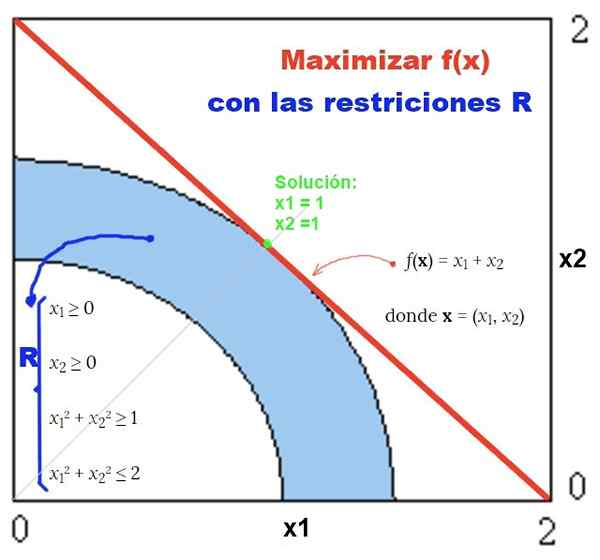Gambar 2. Contoh masalah non-linear dengan batasan non-lineal dan solusi grafisnya. Sumber: f. Zapata.

Latihan

- Latihan 1 (Metode Grafik)

Keuntungan dari perusahaan tertentu tergantung pada jumlah yang dijual produk X dan jumlah yang dijual produk dan, di samping itu, gain ditentukan oleh formula berikut:

Dapat melayani Anda: binomial terkonjugasi: bagaimana itu diselesaikan, contoh, latihan

G = 2 (x - 2)² + 3 (dan - 3)²

Diketahui bahwa jumlah x dan y memiliki batasan berikut:

X≥0; Y≥0 dan x + dan ≤ 7

Tentukan nilai x dan y yang menghasilkan gain maksimum.

Gambar 3. Keuntungan perusahaan dapat dimodelkan secara matematis untuk menemukan keuntungan maksimum dengan pemrograman non -linier. Sumber: Pixabay.

Larutan 

Dalam masalah ini fungsi objektifnya non -linear, sedangkan ketidaksetaraan yang menentukan batasannya. Itu adalah masalah Pemrograman non -linier.

Untuk solusi masalah ini, metode grafik akan dipilih.

Pertama, wilayah solusi akan ditentukan, yang diberikan oleh pembatasan.

Sebagai x≥0; Y≥0, solusinya harus mencari di kuadran pertama bidang XY, tetapi sebagai tambahan harus dipenuhi bahwa x + y ≤ 7, solusinya berada di semiplane yang lebih rendah dari garis x + y = 7.

Wilayah solusi adalah persimpangan kuadran pertama dengan semiplane yang lebih rendah dari garis, yang menimbulkan daerah segitiga di mana solusinya berada. Sama seperti yang ditunjukkan pada Gambar 1.

Di sisi lain, Gain G juga dapat diwakili dalam bidang Cartesian, karena persamaannya adalah elips dengan pusat (2,3).

Elips ditunjukkan pada Gambar 1 untuk beberapa nilai g. Nilai G yang lebih tinggi, keuntungan yang lebih besar.

Ada solusi yang menjadi milik wilayah ini, tetapi jangan memberikan nilai maksimum g, sementara yang lain, seperti g = 92.4, berada di luar zona hijau, yaitu zona solusi.

Kemudian, nilai maksimum g, sedemikian rupa sehingga X e y milik wilayah solusi sesuai dengan: 

Dapat melayani Anda: probabilitas teoretis: cara mengeluarkannya, contoh, latihan

G = 77 (gain maksimum), yang terjadi untuk x = 7 e y = 0. 

Menariknya, keuntungan maksimum terjadi ketika jumlah penjualan produk dan batal, sedangkan jumlah produk x mencapai nilai terbesar.

- Latihan 2 (Metode Analitik: Pengganda Lagrange) 

Temukan solusi (x, y) yang membuat fungsi f (x, y) = x² + 2 dan² menjadi maksimal di wilayah G (x, y) = x² + Dan² - 1 = 0.

Larutan

Ini jelas merupakan masalah pemrograman non-linear, karena baik fungsi objektif f (x, y) dan pembatasan g (x, y) = 0, bukan kombinasi linier dari variabel x dan y.

Metode LaGrange Multipliers akan digunakan, yang pertama -tama memerlukan mendefinisikan fungsi lagrange l (x, y, λ):

L (x, y, λ) = f (x, y) - λ g (x, y) = x² + 2 dan² - λ (x² + Dan² - 1) 

Di mana λ adalah parameter yang disebut Pengganda Lagrange.

Untuk menentukan nilai ekstrem fungsi objektif f, di wilayah solusi yang diberikan oleh pembatasan g (x, y) = 0, langkah -langkah ini diikuti:

-Temukan turunan parsial dari fungsi lagrange l, sehubungan dengan x, y, λ.

-Nol setiap turunan.

Di sini urutan operasi ini:

1. ∂l/∂x = 2x - 2λx = 0
2. ∂l/∂y = 4y - 2λy = 0
3. ∂l/∂λ = -(x² + Dan² - 1) = 0

Solusi sistem yang mungkin

Solusi yang mungkin dari sistem ini adalah λ = 1 untuk memenuhi persamaan pertama, dalam hal ini y = 0 untuk memenuhi yang kedua.

Solusi ini menyiratkan bahwa x = 1 atau x = -1 sehingga persamaan ketiga terpenuhi. Dengan cara ini dua solusi S1 dan S2 telah diperoleh:

S1: (x = 1, y = 0)

S2: (x = -1, y = 0).

Alternatif lainnya adalah bahwa λ = 2 untuk persamaan kedua untuk dipenuhi, terlepas dari nilainya dan.

Itu dapat melayani Anda: batas fermat: apa yang terdiri dari dan latihan diselesaikan

Dalam hal ini, satu -satunya cara untuk persamaan pertama untuk dipenuhi adalah bahwa x = 0. Mempertimbangkan persamaan ketiga, hanya ada dua solusi yang mungkin, yang akan kami sebut S3 dan S4:

S3: (x = 0, y = 1)

S4: (x = 0, y = -1)

Untuk mengetahui solusi mana yang memaksimalkan fungsi objektif, lanjutkan untuk mengganti di f (x, y):

S1: F (1, 0) = 1² + 2.0² = 1

S2: f (-1, 0) = (-1)² + 2.0² = 1

S3: f (0, 1) = 0² + 2.1² = 2

S4: f (0, -1) = 0² + dua puluh satu)² = 2

Kami menyimpulkan bahwa solusi yang memaksimalkan f, ketika x dan y milik keliling g (x, y) = 0 adalah s3 dan s4.

Pasangan nilai (x = 0, y = 1) y (x = 0, y = -1) Maksimalkan f (x, y) di wilayah solusi g (x, y) = 0.

- Latihan 3 (gradien nol)

Temukan solusi (x, y) untuk fungsi objektif:

f (x, y) = x² + 2 dan²

Menjadi maksimal di wilayah G (x, y) = x² + Dan² - 1 ≤ 0.

Larutan

Latihan ini mirip dengan Latihan 2, tetapi wilayah solusi (atau pembatasan) meluas ke daerah interior keliling G (x, y) = 0, yaitu ke lingkaran G (x, y) ≤ 0. Ini termasuk keliling dan wilayah dalamnya.

Solusi perbatasan sudah ditentukan dalam Latihan 2, tetapi perlu untuk menjelajahi wilayah dalam.

Untuk melakukan ini, gradien fungsi f (x, y) harus dihitung dan sama dengan nol, untuk mencari nilai ekstrem di wilayah solusi. Ini setara dengan menghitung turunan parsial F sehubungan dengan X dan masing -masing dan menyamakan nol:

∂f/∂x = 2 x = 0

∂f/∂y = 4 y = 0

Sistem persamaan ini memiliki satu -satunya solusi (x = 0, y = 0) yang termasuk dalam lingkaran G (x, y) ≤ 0.

Mengganti nilai ini dalam fungsi F Fungsi:

f (0, 0) = 0

Kesimpulannya, nilai maksimum yang mengambil fungsi di wilayah solusi adalah 2 dan terjadi pada batas wilayah solusi, untuk nilai (x = 0, y = 1) y (x = 0, y = -1).

 Referensi

1. Avriel, m. 2003. Pemrograman nonlinier. Dover Publishing.
2. Bazaraa. 1979. Pemrograman nonlinier. John Wiley & Sons.
3. Bertsekas, d. 1999. Program Nonlinear: Edisi ke -2. Athena Scientific.
4. Nocedal, J. 1999. Optimasi numerik. Springer-Verlag.
5. Wikipedia. Pemrograman non -linier. Pulih dari: is.Wikipedia.com