Halaman rumah
Matematika
Batasi properti (dengan contoh)

Matematika

Batasi properti (dengan contoh)

1121
66
Ernesto Mueller

Itu Batasi properti Mereka adalah himpunan aturan dan prosedur aljabar yang digunakan untuk menentukannya. Konsep batas sangat penting untuk perhitungan dan menemukan nilainya tidak harus menjadi tugas yang rumit, asalkan propertinya ditangani dengan mudah.

Di bawah ini adalah daftar yang paling penting, disertai dengan contoh aplikasi.

Batas dan propertinya adalah dasar perhitungan. Batas yang sangat istimewa ditunjukkan pada gambar: turunan dari fungsi f (x)

Biarkan b, c, n, a dan b bilangan real, dan F Dan G Fungsi seperti itu yang memverifikasi yang berikut:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Maka Anda memiliki properti berikut:

1. Batas penggantian langsung

Pada contoh pertama, batas fungsi f ketika x → c dapat dihitung secara langsung mengganti x = c dalam fungsi. Jika fungsinya ada pada x = C, maka batasnya adalah:

$\lim_x \rightarrow c f(x)=f(c)$ Tetapi tidak harus fungsi harus didefinisikan pada x = c sehingga batasnya ada. Idenya adalah untuk mendekati sebanyak yang Anda inginkan dengan nilai x = c dan lihat apa yang terjadi dengan fungsi dalam kasus itu.

Contoh

Temukan batas f (x) = x² Saat x → 4

Larutan

Batas dipecahkan hanya dengan mengganti x = 4 dalam f (x) = x², Karena tidak ada ketidaknyamanan dalam menjalankan operasi:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Keunikan batas

Jika batas fungsi f (x) saat x → c ada dan bernilai l, batas tersebut unik.

Oleh karena itu, batas lateral, yaitu ketika x → c^- (Baca “X cenderung C dari kiri”) dan saat x → c⁺(Bunyinya “X cenderung C di sebelah kanan”), keduanya ada dan memiliki nilai yang sama l, bahkan jika fungsi tidak didefinisikan dalam x = c.

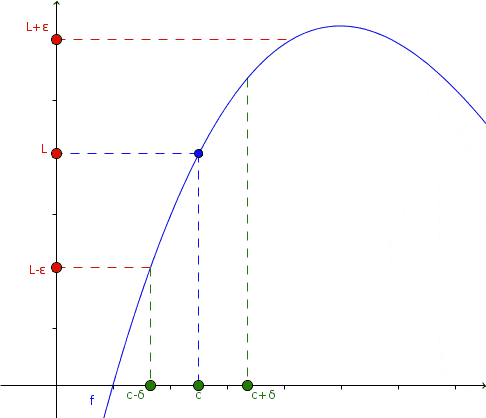Dalam animasi ini, konsep batas disajikan: Ketika x cenderung ke nilai c tertentu, mendekati baik di sebelah kiri dan kanan, nilai fungsi cenderung l. Belum tentu fungsi didefinisikan dalam x = c. Sumber: Wikimedia Commons.

Dalam animasi pendekatan ini diamati dan apa yang terjadi dengan fungsi dalam kasus itu: apakah itu mendekat di sebelah kiri dan di sebelah kanan untuk x = c, nilai fungsi pada gilirannya dekat dengan l.

Dapat melayani Anda: kotak minimum

Secara matematis mengungkapkan cara ini:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Batas lateral memungkinkan untuk mengetahui kapan batas ada atau tidak, karena jika mereka tidak ada atau jika mereka berbeda, dapat dipastikan bahwa batas fungsi ketika x → c tidak ada.

Contoh

Hitung batas f (x) ketika x → 1 jika ada, di mana f (x) diberikan oleh:

Larutan

Ini adalah fungsi berdasarkan bagian atau didefinisikan pada potongan, yang terdiri dari baris 4 -x untuk nilai x < 1 y en la parábola 4 - x² Ketika x sama dengan 1 atau lebih besar dari 1.

Kita dapat mendekati x = 1 dari kiri, dalam hal ini bagian fungsi yang valid untuk x diambil<1:

Karena batas lateral adalah sama, maka batas fungsi ketika x → 1 ada dan bernilai 3.

3. Konstan

Batas konstanta adalah nilai konstanta tersebut, terlepas dari nilai yang dimaksud variabel:

$\lim_x\rightarrow cb=b .$

Contoh

Menghitung:

$\lim_x\rightarrow 1\pi$ Larutan

$\lim_x\rightarrow 1\pi= \pi$

4. Batas fungsi identitas

Jika f (x) = x, selalu dipenuhi itu:

$\lim_x\rightarrow cx=c$

Contoh

Menghitung:

$\lim_x\rightarrow 2x$ Larutan

$\lim_x\rightarrow 2x=2$

5. Batas produk konstanta oleh suatu fungsi

Dalam hal ini, konstanta keluar dari batas dan bergerak untuk melipatgandakannya, seperti ini:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Contoh

Hitung, jika ada, batas berikut:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Larutan

Konstanta 5 berada di luar melipatgandakan batas dan properti pengganti diterapkan:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Batas jumlah

Batas jumlah dua fungsi F Dan G Itu adalah jumlah batas:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Contoh

Temukan batas berikut jika ada:

Dapat melayani Anda: Teori Set: Karakteristik, Elemen, Contoh, Latihan

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Larutan

Properti dari jumlah batas diterapkan terlebih dahulu dan kemudian penggantian langsung, karena operasi tidak menimbulkan kesulitan:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Batas pengurangan

Dalam kasus batas pengurangan dua fungsi, lanjutkan dengan cara analog bahwa untuk jumlah: batas pengurangan adalah pengurangan batas:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Contoh

Hitung batas berikut:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Larutan

Properti dari batas pengurangan dua fungsi diterapkan dan kemudian penggantian langsung, karena semua operasi dapat dilakukan tanpa masalah:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Batas produk

Batas produk dari dua fungsi F Dan G Ini adalah produk dari batas:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Contoh

Hitung batas ini:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Larutan

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Rasio hasil bagi

Batas rasio dua fungsi F Dan G Ini adalah hasil bagi batas, asalkan batas g (x) ketika x → c berbeda dari 0, karena pembagian dengan 0 tidak ditentukan. Jadi:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Contoh

Hitung, jika ada, nilai dari batas berikut:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Larutan

Dalam contoh pertama properti batas properti diterapkan, untuk mendapatkan hasil bagi batas:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Properti pengganti sekarang diterapkan untuk menemukan setiap batas:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Dan karena B ≠ 0, batas yang dicari adalah hasil bagi A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Membatasi

Batas kekuatan eksponen N, setara dengan batas yang dinaikkan dengan kekuatan tersebut, sebagai berikut:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Kasus 1: Batas kekuatan x

Jika Anda memiliki, misalnya, batas daya x, hasilnya:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

Menurut Properti 4, batas ini adalah:

Dapat melayani Anda: analogi numerik: jenis, aplikasi dan latihan

$\lim_x \rightarrow c x^n=c^n$

Kasus 2: Batas Root

Akar N-ini dapat ditulis dalam bentuk eksponen fraksional, karenanya:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Penting: Jika indeks root bahkan, perlu bahwa batas f (x) ketika x → c lebih besar dari atau sama dengan 0, karena tidak ada pasangan nyata dari jumlah negatif.

Contoh

Tentukan, menerapkan properti sebelumnya, batas berikut jika ada:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Solusi untuk

Dengan properti batas kekuatan dan substitusi langsung yang diperoleh:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Solusi b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

sebelas. Membatasi

Untuk menemukan batas Basis Eksponensial B dan Eksponen F (x), dasar fungsi fungsi f (x) harus dinaikkan sebagai berikut:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Contoh

Temukan apakah ada batasan berikut:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Larutan

Di batas ini basis adalah angka E dan fungsi f (x) = x², Oleh karena itu Anda harus terlebih dahulu menghitung batas x² Saat X cenderung 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Kemudian properti dari batas eksponensial diterapkan:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Batas fungsi potensial eksponensial

Batas ketika x → C dari fungsi f (x), yang pada gilirannya meningkat ke fungsi lain g (x) diekspresikan oleh:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Contoh

Hitung batas berikut, jika ada:

$\lim_x \rightarrow -1 (x-1)^^2x$

Larutan

Untuk menerapkan properti sebelumnya, mereka pertama kali diidentifikasi f (x) = x-1 dan g (x) = 2x dan kemudian batas masing-masing dihitung:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Akhirnya:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referensi

Ayres, f. 2000. Perhitungan. 5ed. MC Graw Hill.
Leithold, l. 1992. Perhitungan dengan geometri analitik. Harla, s.KE.
Teks Matematika Gratis. Batas. Pulih dari: matematika.Liibretexts.org.
Mathemovil. Hukum dan Batasi Properti. Pulih dari: matemovil.com.
Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan. Meksiko: Pendidikan Pearson.
Rumus alam semesta. Batasi properti. Pulih dari: universoformulas.com

Batasi properti (dengan contoh)

1. Batas penggantian langsung

Contoh

Larutan

2. Keunikan batas

Contoh

Larutan

3. Konstan

Contoh

Larutan

4. Batas fungsi identitas

Contoh

Larutan

5. Batas produk konstanta oleh suatu fungsi

Contoh

Larutan

6. Batas jumlah

Contoh

Larutan

7. Batas pengurangan

Contoh

Larutan

8. Batas produk

Contoh

Larutan

9. Rasio hasil bagi

Contoh

Larutan

10. Membatasi

Kasus 1: Batas kekuatan x

Kasus 2: Batas Root

Contoh

Solusi untuk

Solusi b

sebelas. Membatasi

Contoh

Larutan

12. Batas fungsi potensial eksponensial

Contoh

Larutan

Referensi

Artikel Terbaik

Juan Martín Moyë Biography

Juan Martín Moyë (1730 - 1793) adalah seorang imam Prancis yang menunjukkan pengabdian yang kuat kep...

70 frasa gothic terbaik

Frasa gothic terbaik tentang cinta, kematian, kegelapan, penderitaan dan kesedihan. Subkultur Gotik ...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Keunikan batas

$\lim_x\rightarrow 1\pi$ Larutan

$\lim_x\rightarrow 2x$ Larutan

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Contoh

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Larutan

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Larutan

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Larutan

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Contoh

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Larutan

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Kasus 1: Batas kekuatan x

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Larutan

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referensi