Apa pedomannya? (Geometri)

Itu pengarahan Dalam geometri itu terdiri dari kurva, permukaan atau volume yang tetap diperbaiki dan menentukan cara di mana objek geometris terbentuk. Misalnya, dengan garis kurva lain seperti kerucut, dan permukaan revolusi, seperti silinder melingkar lurus didirikan.

Kurva pedoman juga bisa menjadi keliling. Silinder melingkar lurus dapat dibentuk dengan meninggalkan radius ri -r rión ri.

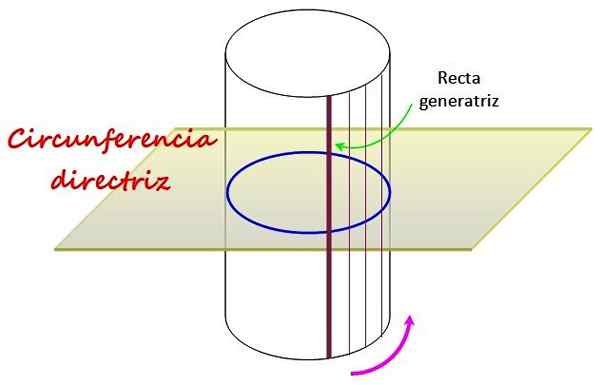
Gambar 1. Silinder melingkar lurus memiliki sebagai panduan lingkaran, di sekitar garis lurus yang disebut generatrix bergerak. Sumber: f. Zapata.

Lingkar, yang berada pada bidang yang ditarik pada gambar, menentukan bentuk permukaan melengkung dari silinder melingkar lurus, yang dihasilkan dengan memutar garis di sekitarnya, disebut generatrix lurus.

Jika kurva bimbingan bukan keliling, tetapi kurva lain, jenis silinder lainnya dihasilkan, seperti silinder elips, yang pedomannya merupakan elips.

Lingkar juga dapat bertindak sebagai pedoman untuk menghasilkan kurva lain, seperti kasus dari Epitrocoid, Kurva dalam bidang yang dihasilkan oleh titik, yang pada gilirannya berada dalam lingkaran yang lebih kecil yang berguling tanpa meluncur, di sekitar pedoman.

Lebih mudah untuk menghargainya secara visual dengan animasi berikut:

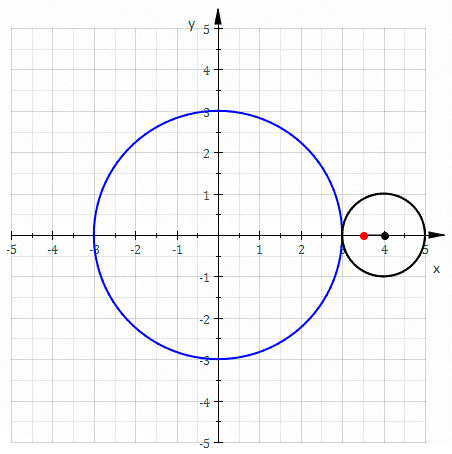Gambar 2. Kurva merah dipanggil Epitrocide dan kurva pedomannya. Sumber: Wikimedia Commons. Sam Derbyshire di Inggris Wikipedia/CC BYS (http: // CreationCommons.Org/lisensi/by-sa/3.0/).

Kurva pedoman pada permukaan silinder

Permukaan silindris diklasifikasikan menurut kurva pedoman mereka dalam silinder:

-Bundar

-Berbentuk bulat panjang

-Parabola

-Hiperbolis

Ketika permukaan silinder memiliki pedoman yang terletak pada bidang yang tegak lurus dengan garis generatrix, persamaan permukaan tersebut sama dengan pedoman pedoman tersebut.

Itu dapat melayani Anda: apa hubungan antara area belah ketupat dan persegi panjang?

Silinder itu termasuk dalam kelompok Permukaan Quidric, yang persamaannya kelas dua dengan tiga variabel. Bentuk umumnya adalah:

Kapak² + Oleh² + CZ² + DXY + EXZ + FYZ + GX + HY + IZ + K = 0

Dimana koefisien a, b, c ... adalah bilangan real.

Silinder adalah badan geometris tiga -dimensi yang paling umum dan berguna yang dapat ditemukan, terutama silinder melingkar lurus, tetapi jenis silinder lain yang dijelaskan di bawah ini juga memiliki aplikasi dalam teknik dan desain.

Silinder melingkar lurus

Pedomannya adalah lingkaran C yang berada dalam bidang tegak lurus terhadap silinder, seperti yang ditunjukkan pada Gambar 1, karena garis generatrix, yang berjalan ke C untuk membentuk permukaan lateral, tegak lurus terhadap c.

Persamaan keliling C pada bidang XY, difokuskan pada asal (0,0) adalah:

X² + Dan² = R²

Di mana r, jari -jari keliling jelas akan menjadi jari -jari silinder. Tinggi h dari silinder memanjang di sepanjang sumbu z, tegak lurus terhadap bidang xy.

Silinder elips

Pedoman ini adalah elips di bidang XY yang berpusat pada asal (0,0), yang persamaannya adalah:

Generatrix adalah garis tegak lurus terhadap bidang XY, yang bergerak di sekitar elips untuk memunculkan permukaan lateral. Elips dapat berada di ketinggian apa pun di pesawat XY.

Misalnya, elips persamaan:

4x² + 9y² = 36

Kurva pedoman yang menimbulkan silinder elips yang persamaannya adalah 4x² + 9y² = 36, ditambah z = 0. Menambahkan ungkapan terakhir ini, jelas bahwa itu adalah permukaannya.

Dapat melayani Anda: Kesalahan pengambilan sampel: Rumus dan persamaan, perhitungan, contoh

Silinder parabola

Dalam hal ini pedomannya adalah perumpamaan, yang dapat dari bentuk y = x². Dengan demikian silinder diarahkan sepanjang sumbu z dan membentuk penumpukan perumpamaan dengan simpul di (0,0) di sepanjang sumbu itu.

Silinder parabola memiliki aplikasi dalam energi matahari, karena beberapa kolektor memiliki cermin dengan cara itu, di mana sinar matahari terkonsentrasi dalam fokus. Titik ini melewati pipa lurus di mana oli mencapai suhu hingga 400 º C.

Silinder hiperbolik

Dalam silinder hiperbolik, persamaan pedoman ini adalah hiperbola yang berpusat pada asal:

Silinder dibentuk ke tumpukan.

Permukaan revolusi

Kurva pedoman permukaan revolusi adalah sumbu revolusi yang sama, garis di sekitar kurva yang bertanggung jawab untuk menghasilkan permukaan.

Kurva yang berputar dapat memiliki bentuk sewenang -wenang, dengan cara ini suatu area dihasilkan seperti yang terlihat dalam animasi ini:

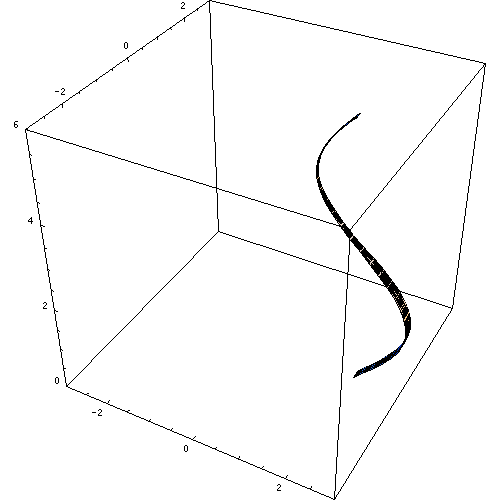Gambar 3. Permukaan revolusi. Sumber: Wikimedia Commons. https: // unggah.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.Gif.

Jika garis lain diputar di sekitar pedoman, silinder melingkar lurus yang sudah akrab diperoleh. Dengan cara yang sama, permukaan revolusi lainnya dapat diperoleh, seperti permukaan kerucut, bola dan revolusi toroidal.

Permukaan kerucut

Permukaan kerucut dihasilkan oleh pergerakan garis generatrix yang selalu melewati kurva datar atau kurva pedoman tetap dan oleh titik tetap yang disebut vertex, yang bukan milik bidang pedoman.

Dapat melayani Anda: Harapan Matematika: Formula, Properti, Contoh, Latihan

Titik atau ujung membagi kerucut menjadi dua bagian, disebut daun-daun salah satu ranting.

Latihan terpecahkan

- Latihan 1

Temukan luas lateral silinder sirkular tinggi tinggi 25 cm, yang kurva pedomannya adalah lingkar radius 6 cm, difokuskan pada asal.

Larutan

Area lateral silinder adalah produk dari panjang pedoman berdasarkan tinggi. Jika R adalah jari -jari keliling dan h adalah ketinggian silinder, area tersebut diberikan oleh:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Latihan 2

Anda memiliki persamaan berikut yang sesuai dengan permukaan kuadrik:

X² + Dan² + 2z² +2xz - 2yz = 1

Tunjukkan permukaan apa itu dan apa persamaan pedoman.

Larutan

Melakukan z = k, di mana k konstan, diperoleh:

X² + Dan² + 2k² +2kx - 2ky = 1

Kami mengatur ulang istilah sebagai berikut:

(X² + 2kx) + (dan²- 2ky) = 1-2k²

Kotak harus², Agar tidak mengubah tanda kurung apa pun:

(X² + 2kx + k² - k² ) + (dan² - 2ky + k² - k²) = 1-2k²

(X² + 2kx + k²) - k²  + (Dan²- 2ky + k²) - k² = 1-2k²

Dengan cara ini tetap:

(x + k)² + (dan - k)² = 1

Seperti persamaan lingkaran tengah (-k, k) dan jari-jari 1, permukaan adalah silinder melingkar lurus, juga dari radio 1, selama garis generatrix tegak lurus terhadap lingkar tersebut.

Misalnya, melakukan k = 0, persamaan dikurangi ke lingkar yang berpusat pada asal (0,0) yang jari -jarinya 1:

X² + Dan² = 1

Referensi

1. Gaussians. Mewakili tiga permukaan dimensi. Pulih dari: Gaussians.com.
2. Kindle, J. Teori dan masalah geometri analitik. Bukit McGraw. Seri Schaum.
3. Permukaan sebagai tempat geometris. Pulih dari: aljabar.FRLP.Utn.Edu.ar.
4. Suárez, m. Permukaan. Diperoleh dari: Subjek.Unq.Edu.ar.
5. Permukaan Quidric. Pulih dari: sistem.fciencias.Unam.MX.