Apa reaktansi kapasitif dan bagaimana menghitungnya?

Itu reaktansi kapasitif Ini adalah resistansi bahwa kondensor, elemen pengatur aliran beban dalam sirkuit arus bolak -balik, menentang bagian arus.

Dalam sirkuit yang dibentuk dari kondensor dan diaktifkan oleh sumber arus bergantian, reaktansi kapasitif X dapat didefinisikan_C sebagai berikut:

X_C = 1 / ωc

Gambar 1. Reaktansi kapasitif adalah bagian dari filter Passabajos dan penutur pembicara. Sumber: Pixabay.

Atau juga:

X_C = 1 / 2πfc

Di mana C adalah kapasitas kapasitor dan Ω adalah frekuensi sudut sumber, terkait dengan frekuensi f melalui:

Ω = 2πf

Reaktansi kapasitif tergantung pada kebalikan dari frekuensi, oleh karena itu pada frekuensi tinggi cenderung kecil, sedangkan pada frekuensi rendah, reaktansi besar.

Unit sistem internasional untuk mengukur reaktansi kapasitif adalah ohm (Ω), asalkan kapasitas kapasitor berada di farad, (disingkat f) dan frekuensi dinyatakan dalam kebalikan dari detik (s^-1).

Sementara beban berlangsung, tegangan dan arus juga ditetapkan melalui kapasitor, yang amplitudo atau nilainya maksimal, masing -masing dilambangkan sebagai v_C dan saya_C, Mereka terkait melalui reaktansi kapasitif yang analog dengan hukum Ohm:

V_C = I_C ⋅ x_C

Dalam kondensor, tegangan tertunda 90º sehubungan dengan arus, atau canggih 90º sehubungan dengan itu, seperti yang disukai. Bagaimanapun frekuensinya sama.

Saat x_C Ini sangat besar, arus cenderung kecil dan membuat nilai x tak terbatas_C, Kondensor berperilaku seperti sirkuit terbuka dan arusnya nol.

[TOC]

Cara menghitung reaktansi kapasitif

Mari kita lihat contoh cara menghitung reaktansi kapasitif: Misalkan kapasitor 6 μF terhubung ke outlet daya bergantian dan frekuensi dan frekuensi F 60 Hz.

Untuk menemukan reaktansi kapasitif, definisi yang diberikan pada awalnya digunakan. Frekuensi sudut Ω diberikan oleh:

Itu dapat melayani Anda: induksi magnetik: formula, bagaimana itu dihitung dan contohnya

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Maka hasil ini diganti dalam definisi:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

Sekarang mari kita lihat amplitudo arus yang beredar di sirkuit. Karena sumbernya menawarkan tegangan amplitudo v_C = 40 V, kami menggunakan hubungan antara reaktansi kapasitif, arus dan tegangan untuk menghitung amplitudo arus atau arus maksimum:

yo_C = V_C / X_C = 40 V / 442.1 ohm = 0.09047 A = 90.5 m a.

Jika frekuensinya menjadi sangat besar, reaktansi kapasitif menjadi kecil, tetapi jika frekuensinya menjadi 0 dan kami memiliki arus searah, reaktansi akan cenderung tidak terbatas.

Tegangan arus dan kondensor

Ketika kondensor terhubung ke sumber arus bergantian, seperti itu berosilasi dan mengubah polaritasnya, kapasitor mengalami beban dan melepaskan secara bergantian.

Untuk frekuensi 60 Hz seperti contoh, tegangannya positif 60 kali per detik, dan negatif 60 kali per detik.

Gambar 2. Sirkuit kondensor sederhana dan sumber arus bergantian. Sumber: f. Zapata.

Dengan meningkatkan tegangan, ia menggerakkan arus dalam satu arah, tetapi jika kondensor mengunduh, arus terjadi di arah yang berlawanan yang menentang yang pertama.

Ya v_C (t) = v_M Sen ωt, mengetahui bahwa kapasitas adalah alasan antara beban dan tegangan, kita akan memiliki beban:

C = q/v → q (t) = cv = cv_M SEN ωt

Dan memiliki beban tergantung pada waktu, kita akan memiliki arus, yang merupakan turunan dari itu:

yo_C(t) = CV_M Ω cos ωt

Tetapi payudara dan kosinus terkait melalui: cos α = sin (α + π/2), oleh karena itu:

yo_C(t) = CV_M Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Dengan i_C = Cv_C Ω

Seperti yang dapat dilihat, ada perbedaan 90º kemajuan arus sehubungan dengan tegangan, seperti yang dikomentari di awal.

Dapat melayani Anda: Millikan Eksperimen: Prosedur, Penjelasan, Pentingnya

Dalam deskripsi jenis sirkuit ini, konsep Fasor, yang sangat mirip dengan vektor dan memungkinkan untuk mewakili dalam bidang kompleks jumlah bergantian seperti arus, tegangan atau impedansi.

Gambar berikut menunjukkan, di sebelah kanan, tegangan dan arus fasor dalam kapasitor, yang membentuk sudut 90º, yang merupakan jeda antara keduanya.

Di sebelah kiri adalah grafik masing -masing, dari amplitudo yang berbeda, tetapi frekuensi yang sama. Pada waktunya, arus maju ke tegangan dan ketika ini maksimum, arus nol dan ketika tegangan nol, arus maksimum tetapi dengan polaritas terbalik terbalik.

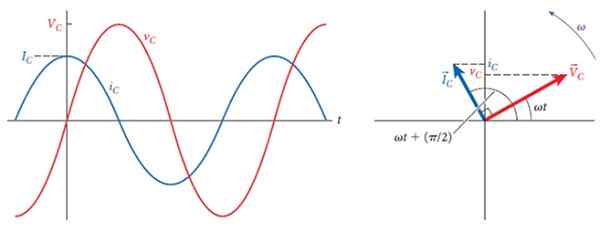Gambar 3. 90º tertinggal antara arus dan tegangan melalui kapasitor. Sumber: Bauer, W.

Impedansi kondensor kompleks

Dalam sirkuit dengan resistensi, kapasitor dan induktansi, reaktansi adalah bagian imajiner dari impedansi z, jumlah kompleks yang dalam sirkuit arus bolak.

Faktanya, impedansi sirkuit didefinisikan sebagai alasan antara tegangan dan arus:

Z = v / i

Untuk kapasitor atau kapasitor, impedansinya diberikan oleh hasil bagi:

Z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

Cara mengekspresikan tegangan dan arus sebagai fasor adalah untuk menunjukkan amplitudo dan sudut fase (bentuk kutub):

v (t) = v_C ∠ 0º

I (t) = i_C ∠ 90º

Karena itu:

Z_C = V_C ∠ 0º / i_C ∠ 90º = (v_C / YO_C) ∠ 0º -90º =

= V_C / CV_C Ω ∠ -90º = (1/ ωc) ∠ -90º =

Z_C = (- j) x_C

Yaitu, impedansi kondensor adalah reaktansi kapasitifnya dikalikan dengan negatif dari unit imajiner.

Impedansi Sirkuit Seri RC

Impedansi sirkuit arus bolak -balik dengan resistansi, kapasitor dan induktor juga dapat diwakili secara binomi dengan:

Ini dapat melayani Anda: Hukum Termodinamika Pertama: Rumus, Persamaan, Contoh

Z = r + jx

Dalam persamaan ini, R mewakili resistansi, yang sesuai dengan bagian nyata, J adalah unit imajiner dan x adalah reaktansi, yang dapat berupa kapasitif atau induktif atau kombinasi keduanya, jika elemen -elemen ini hadir pada saat yang sama di sirkuit.

Jika sirkuit berisi resistensi dan kapasitor serial, impedansinya adalah:

Z = z_R + Z_C    

Seperti dalam tegangan resistansi dan arus dalam fase, impedansi resistif hanyalah nilai resistansi r.

Dalam kasus impedansi kapasitif, kita telah melihat z_C = -Jx_C , Oleh karena itu impedansi sirkuit RC adalah:

Z = r - jx_C = R - j (1/ ωc)

Misalnya di sirkuit yang ditunjukkan di bawah ini, yang sumbernya dari bentuk:

100 V ⋅ sen (120πt)

Mengamati bahwa Ω = 120π, impedansi adalah:

Z = 83.0 - j [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

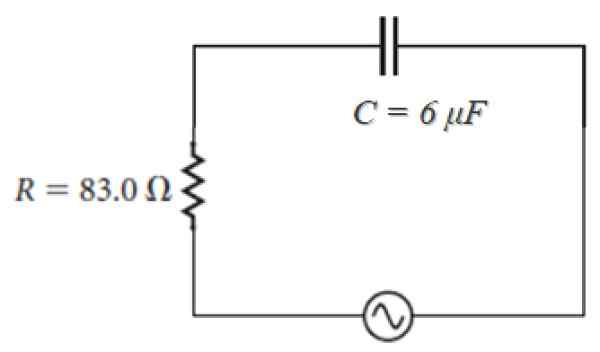Gambar 4. Seri Sirkuit RC dengan sumber arus bergantian. Sumber: f. Zapata.

Aplikasi reaktansi kapasitif

Pasa filter tinggi, filter low pass, sirkuit jembatan untuk mengukur kapasitansi dan induktansi dan sirkuit kulkas adalah di antara aplikasi sirkuit utama yang mengandung reaktansi kapasitif, dalam kombinasi dengan induktansi dan resistensi listrik.

Dalam peralatan suara, beberapa speaker dilengkapi dengan jenis jenis yang terpisah Woofer (lebih besar) untuk frekuensi rendah dan Tweeter atau tanduk kecil untuk frekuensi tinggi. Dengan cara ini kinerja dan kualitas audio meningkat.

Mereka digunakan kapasitor yang mencegah kedatangan frekuensi rendah di tweeter, sementara induktor ditambahkan di woofer untuk menghindari sinyal frekuensi tinggi, karena induktansi memiliki reaktansi yang sebanding dengan frekuensi: x x_L = 2πfl.

Referensi

1. Alexander, c. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.
2. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 2. MC Graw Hill.
3. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.