Apa itu kecepatan linier? (Dengan latihan terpecahkan)

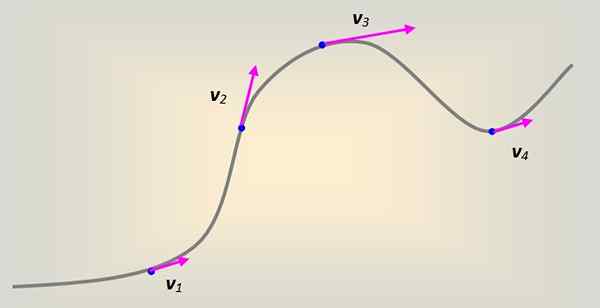
Itu Kecepatan linier Itu didefinisikan sebagai apa yang selalu tangensial terhadap lintasan diikuti oleh partikel, terlepas dari itu. Jika partikel selalu bergerak dalam lintasan bujursangkar, tidak ada masalah yang membayangkan bagaimana vektor kecepatan menyertai garis lurus ini.

Namun, secara umum gerakan dilakukan pada kurva secara sewenang -wenang. Setiap bagian dari kurva dapat dimodelkan seolah -olah itu adalah bagian dari lingkaran radio ke, yang di setiap titik bersinggungan dengan jalan diikuti.

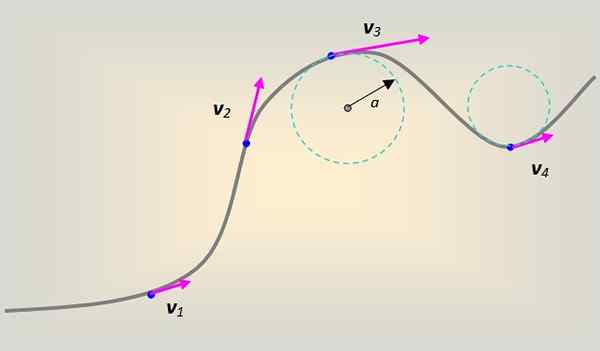Gambar 1. Kecepatan linier pada ponsel yang menggambarkan lintasan lengkung. Sumber: Made sendiri.

Dalam hal ini, kecepatan linier menyertai tangensial dan setiap saat ke kurva di setiap titiknya.

Kecepatan linier instan secara matematis adalah turunan dari posisi sehubungan dengan waktu. Menjadi R vektor posisi partikel dalam sekejap T, Maka kecepatan linier diberikan oleh ekspresi:

v = R'(T) = dR / dt

Ini berarti bahwa kecepatan linier atau kecepatan tangensial, seperti yang juga disebut, tidak lain adalah perubahan posisi sehubungan dengan waktu.

[TOC]

Kecepatan linier dalam gerakan melingkar

Ketika gerakan berada di lingkar, kita dapat pergi ke samping partikel di setiap titik dan melihat apa yang terjadi dalam dua arah yang sangat khusus: salah satunya adalah yang selalu menunjuk ke tengah. Ini adalah alamatnya radial.

Arah penting lainnya adalah arah yang terjadi di lingkar, ini adalah alamatnya tangensial Dan kecepatan linier selalu memilikinya.

Dapat melayani Anda: Tekanan Manometrik: Penjelasan, Rumus, Persamaan, Contoh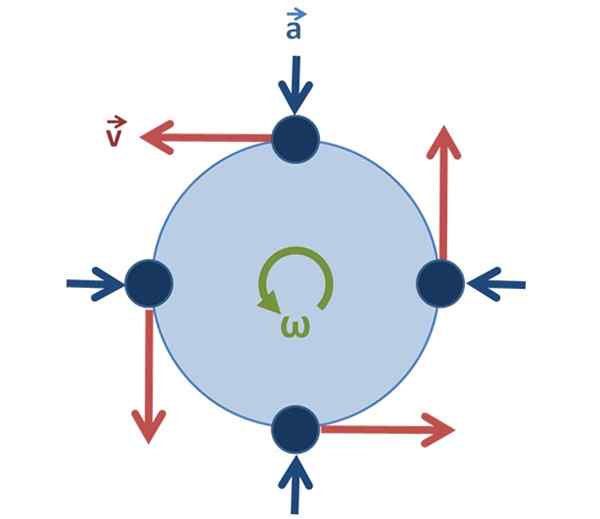Gambar 2. Gerakan melingkar seragam: vektor kecepatan mengubah arah dan arah saat partikel berputar, tetapi besarnya sama. Sumber: Asli oleh pengguna: brews_ohare, svged oleh pengguna: sjlegg [cc by-sa 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)].

Dalam kasus gerakan melingkar seragam, penting ya tetap tidak berubah.

Untuk gerakan ini posisi sebagai fungsi waktu diberikan oleh S (t), Di mana S Apakah dia Tourd Arc Dan T Sudah waktunya. Dalam hal ini, kecepatan sesaat diberikan oleh ekspresi V = DS/DT Dan itu konstan.

Jika besarnya kecepatan juga bervariasi (kita sudah tahu bahwa arah selalu melakukannya, jika tidak, ponsel tidak dapat berputar), kita menghadapi gerakan melingkar yang bervariasi, di mana ponsel selain berputar, itu dapat berhenti atau mempercepat.

Kecepatan linier, kecepatan sudut dan akselerasi sentripetal

Gerakan partikel juga dapat dilihat dari sudut pandang sudut menyapu, Alih -alih melakukannya dari tujuan yang dilalui. Dalam hal ini ada pembicaraan tentang Kecepatan sudut. Untuk gerakan di lingkaran radio R, Ada hubungan antara busur (dalam radian) dan sudut:

S = r θ

Turun sehubungan dengan kedua belah pihak:

ds/dt = r (dθ/dt)

Memanggil turunan θ sehubungan dengan T sebagai Kecepatan sudut Dan menunjukkannya dengan huruf Yunani Ω "omega", Anda memiliki hubungan ini:

v = ΩR

Percepatan sentripetal

Setiap gerakan melingkar percepatan sentripetal, yang selalu diarahkan ke pusat keliling. Dia berhati -hati bahwa kecepatan berubah untuk bergerak dengan partikel saat berubah.

Itu dapat melayani Anda: Kurva Kalibrasi: Untuk apa itu, bagaimana melakukannya, contoh

Percepatan sentripetal ke_C salah satu ke_R Itu selalu menunjuk ke tengah (lihat Gambar 2) dan terkait dengan kecepatan linier dengan cara ini:

ke_C = v² /R

Dan dengan kecepatan sudut sebagai:

ke_C = (ΩR)² /R = Ω²R

Untuk gerakan melingkar yang seragam, posisinya S (t) Itu dari bentuk:

S (t) = jadi+ vt

Selain itu, gerakan melingkar yang bervariasi harus memiliki komponen akselerasi yang disebut Percepatan tangensial ke_T, yang berkaitan dengan mengubah besarnya kecepatan linier. Ya ke_T  itu konstan, Posisinya adalah:

S (t) = s_{salah satu} + v_{salah satu}T + ½ a_TT²

Dengan v_{salah satu} Seperti kecepatan awal.

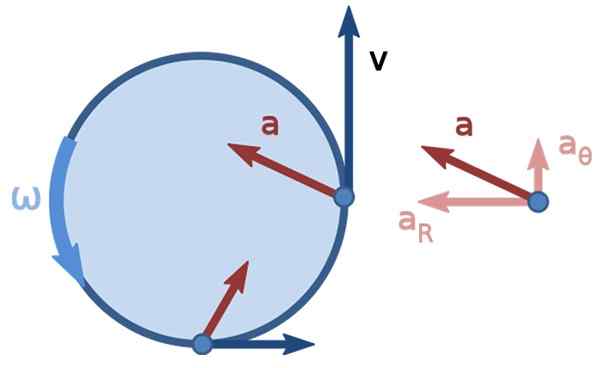Gambar 3. Gerakan melingkar non -uniform. Sumber: nonuniform_circular_motion.PNG: Brews Oharedorivative Work: Kooning Jons [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)].

Latihan Kecepatan Linier Terpecahkan

Latihan terpecahkan berkontribusi untuk mengklarifikasi penggunaan konsep dan persamaan yang tepat.

-Latihan diselesaikan 1 

Serangga bergerak pada setengah lingkaran radius r = 2 m, mulai dari istirahat pada titik beberapa saat meningkatkan kecepatan liniernya, pada tingkat p m/s². Temukan: a) Setelah jam berapa mencapai titik B, b) vektor kecepatan linier pada saat itu, c) percepatan vektor pada saat itu.

Gambar 4. Serangga dimulai dari A dan mencapai B pada lintasan setengah lingkaran. Ini memiliki kecepatan linier. Sumber: Made sendiri.

Larutan

a) Pernyataan tersebut menunjukkan bahwa akselerasi tangensial adalah konstan dan bernilai π m/s², Maka valid untuk menggunakan persamaan untuk gerakan yang bervariasi secara seragam:

S (t) = s_{salah satu} + v_{salah satu}T + ½ a_T.T²

Dengan s_{salah satu} = 0 dan v_{salah satu} = 0:

S (t) = ½ a_T.T²

S = πR (Setengah dari panjang lingkar)

T = (2. πR /ke_T) ^½ S = (2π.2 /π)^½S = 2 detik

B) v (t) = v_{salah satu} + ke_T. T = 2π MS

Ketika pada titik B, vektor kecepatan linier menunjuk ke arah vertikal ke bawah ke arah (-Dan):

Dapat melayani Anda: apa konstanta dielektrik?

v (t) = 2π MS(-Dan)

c) Akselerasi tangensial sudah dimiliki, akselerasi sentripetal hilang untuk memiliki vektor kecepatan ke:

ke_C = v² / R = (2π)² / 2 m/ s² = 2π² MS²

ke = a_C (-X) + a_T (-Dan) = 2π²(-X)+ π (-Dan) MS²

-Latihan diselesaikan 2

Partikel berubah dalam lingkaran radio 2.90 m. Pada saat tertentu akselerasinya bernilai 1.05 m/s² ke arah sedemikian rupa yang membentuk 32 dengan arah gerakannya. Temukan kecepatan linier Anda di: a) momen ini, b) 2 detik kemudian, dengan asumsi bahwa akselerasi tangensial konstan.

Larutan

A) Direktorat Gerakan justru alamat tangensial:

ke_T = 1.05 m/s² . cos 32º = 0.89 m/s² ; ke_C = 1.05 m/s² . Sen 32º = 0.56 m/s²

Kecepatannya jelas ke_C = v² / R sebagai:

v = (r.ke_C)^1/2  = 1.27 m/s

b) Persamaan untuk gerakan yang bervariasi secara seragam valid sebagai berikut: V = V_{salah satu} + ke_TT = 1.27 + 0.89 .2² m/s = 4.83 m/s

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 84-88.
2. Figueroa, d. Seri Fisik untuk Sains dan Teknik. Volume 3. Edisi. Kinematika. 199-232.
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6^th… Ed Prentice Hall. 62-64.
4. Gerakan relatif. Pulih dari: kursus.Lumenarning.com
5. Wilson, J. 2011. Fisika 10. Pendidikan Pearson. 166-168.