Karakteristik, persamaan, dan contoh hak -hak oblicual

Itu Garis miring Mereka adalah yang cenderung, baik sehubungan dengan permukaan datar atau garis lain yang menunjukkan alamat tertentu. Sebagai contoh, pertimbangkan tiga garis yang ditarik dalam bidang yang muncul pada gambar berikut.

Kami tahu posisi relatif masing -masing karena kami membandingkannya dengan garis referensi, yang biasanya merupakan Sumbu x yang menunjukkan horizontal.

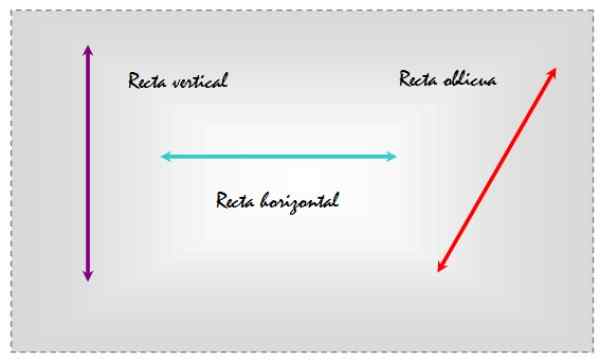
Gambar 1. Garis vertikal, horizontal dan miring di bidang yang sama. Sumber: f. Zapata.

Dengan cara ini, memilih referensi horizontal, garis kiri vertikal, pusatnya horizontal dan yang di sebelah kanan miring, karena cenderung sehubungan dengan garis referensi harian.

Sekarang, garis -garis yang berada di bidang yang sama, seperti permukaan kertas atau layar, menempati posisi yang berbeda relatif satu sama lain, tergantung pada apakah mereka berpotongan atau tidak. Dalam kasus pertama mereka kering lurus, sedangkan di yang kedua, mereka paralel.

Di sisi lain, garis pengeringan juga bisa menjadi garis lurus miring atau tegak lurus. Dalam kedua kasus tersebut, kemiringan garis berbeda, tetapi garis miring terbentuk di antara mereka sendiri α dan β sudut, selain 90º, sedangkan sudut yang ditentukan oleh garis tegak lurus selalu 90º.

Dalam gambar berikut, definisi ini dirangkum:

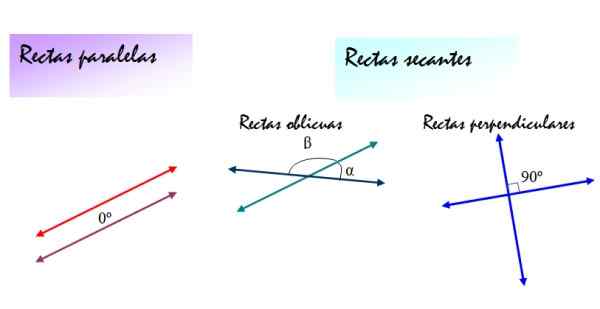Gambar 2. Posisi relatif antara garis: paralel, miring dan tegak lurus berbeda pada sudut yang membentuk satu sama lain. Sumber: f. Zapata.

[TOC]

Persamaan

Untuk mengetahui posisi relatif dari garis di pesawat, perlu mengetahui sudut yang mereka bentuk satu sama lain. Perhatikan bahwa garisnya adalah:

Dapat melayani Anda: perhitungan pendekatan menggunakan diferensial

Paralel: Jika mereka memiliki kemiringan yang sama (arah yang sama) dan tidak pernah berpotongan, jadi poin mereka sama.

Kebetulan: Ketika semua poin mereka bertepatan dan karenanya memiliki kemiringan yang sama, tetapi jarak antara poin mereka adalah nol.

Secantes: Jika anting -anting Anda berbeda, jarak antara titik -titiknya bervariasi dan persimpangan adalah satu titik.

Jadi, cara mengetahui apakah dua garis di pesawat kering atau paralel adalah melalui kemiringannya. Kriteria paralelisme dan tegak lurus dari garis adalah sebagai berikut:

Menjadi dua baris l₁ dan saya₂ milik pesawat, yang tertunda masing -masing m₁ dan m₂. Garis -garis ini paralel jika m₁ = m₂ dan mereka tegak lurus saat m₁= -1/m₂

Jika mengetahui kemiringan dua garis di pesawat, tidak ada kriteria di atas yang terpenuhi, kami menyimpulkan bahwa garis itu miring. Mengetahui dua titik garis, lereng dihitung segera, seperti yang akan kita lihat di bagian selanjutnya.

Anda dapat mengetahui apakah dua garis kering atau paralel menemukan persimpangan mereka, memecahkan sistem persamaan bentuk itu: jika ada solusi mereka kering, jika tidak ada paralelnya, tetapi jika solusinya tak terbatas, garisnya kebetulan.

Namun, kriteria ini tidak memberi tahu kami tentang sudut antara garis -garis ini, bahkan jika mereka memiliki persimpangan.

Untuk mengetahui sudut di antara garis -garis, dua vektor dibutuhkan atau Dan v itu milik masing -masing. Dengan demikian dimungkinkan untuk mengetahui sudut yang mereka bentuk melalui produk skalar dari vektor, didefinisikan dengan cara ini:

atau•v =atau.v.cos α

Persamaan garis di pesawat

Garis di pesawat Cartesian dapat diwakili dalam beberapa cara, seperti:

Itu dapat melayani Anda: Persamaan Parabola Umum (Contoh dan Latihan)

-Formulir yang tertunda: Ya M Itu adalah kemiringan garis dan B Ini adalah persimpangan garis dengan sumbu vertikal, persamaan garis adalah y = mx +b.

-Persamaan Umum untuk Garis Lurus: Kapak + oleh + c = 0, Di mana M = a/b Itu adalah lereng.

Di bidang Cartesian, garis vertikal dan horizontal adalah kasus khusus dari persamaan garis.

-Garis vertikal: x = a

-Garis horizontal: y = k

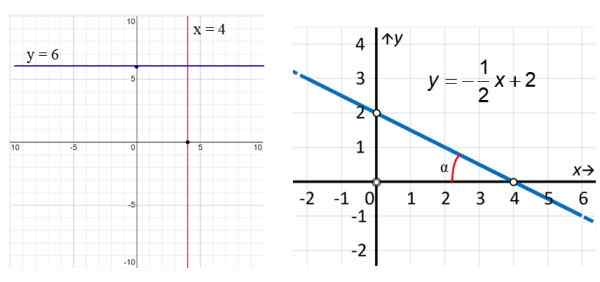Gambar 3. Di sebelah kiri garis vertikal x = 4 dan garis horizontal y = 6. Di sebelah kanan contoh garis miring. Sumber: f. Zapata.

Dalam contoh Gambar 3, garis merah vertikal memiliki persamaan x = 4, sedangkan garis sejajar dengan sumbu x (biru) memiliki persamaan y = 6. Adapun baris yang tepat, kami melihat bahwa itu miring dan menemukan persamaannya kami menggunakan titik -titik yang disorot pada gambar: (0.2) dan (4.0) dengan cara ini:

M = (dan₂ - Dan₁) / (X₂ - X₁) = (2 - 0) / (0 - 4) = - ½

Potongan garis ini dengan sumbu vertikal y = 2, Seperti dicatat dari grafik. Dengan informasi ini:

y = (-½) x+2

Menentukan sudut kemiringan sehubungan dengan sumbu x sederhana. Aku merasakannya:

α = arctg (2/4) = 26.6

Oleh karena itu sudut positif dari sumbu x ke garis adalah: 180º - 26.6 = 153.4

Contoh garis miring

Gambar 4. Contoh garis miring. Sumber: Ian Patterson Wrathful [cc by (https: // createveCommons.Org/lisensi/oleh/2.0)]. Menara condong Pisa. Pixabay.

Garis miring muncul di banyak tempat, ini adalah masalah memperhatikan untuk menemukannya dalam arsitektur, olahraga, kabel pasokan listrik, pipa dan di banyak tempat lagi. Di alam, garis miring juga ada, seperti yang akan kita lihat di bawah:

Dapat melayani Anda: aturan derivasi (dengan contoh)

Sinar cahaya

Cahaya matahari menyebar dalam garis lurus, tetapi bentuk bumi bulat mempengaruhi cara sinar matahari mempengaruhi permukaan.

Pada gambar di bawah ini kita dapat dengan jelas menghargai bahwa sinar matahari mempengaruhi tegak lurus di daerah tropis, tetapi sebaliknya mereka tiba secara miring ke permukaan di daerah beriklim dan di kutub.

Oleh karena itu sinar matahari menempuh jarak yang lebih panjang melalui atmosfer dan juga panas menyebar di permukaan yang lebih besar (lihat gambar). Hasilnya adalah area yang dekat dengan kutub lebih dingin.

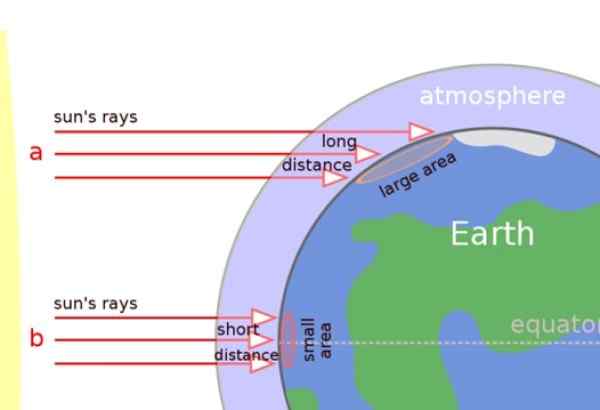Gambar 5. Sinar matahari secara miring mempengaruhi zona beriklim dan kutub, namun mereka kurang lebih tegak lurus di daerah tropis. Sumber: Wikimedia Commons.

Garis yang tidak berada di bidang yang sama

Ketika dua garis tidak berada di bidang yang sama, mereka masih bisa miring atau dipuji, seperti yang juga diketahui. Dalam hal ini, direkturnya tidak paralel, tetapi bukan milik bidang yang sama, garis -garis ini tidak memiliki persimpangan.

Misalnya, garis pada gambar yang tepat jelas di bidang yang berbeda. Jika mereka melihat dari atas itu diamati bahwa mereka secara efektif menyeberang, tetapi mereka tidak memiliki titik yang sama. Di sebelah kanan kita melihat roda sepeda, yang sinarnya tampak menyeberang saat mereka melihat lurus ke depan.

Gambar 6. Garis miring milik bidang yang berbeda. Sumber: kiri f. Zapata, pixabay kanan.

Referensi

1. Geometri. Direktur Vektor Line. Pulih dari: juanbragado.adalah.
2. Larson, r. 2006. Perhitungan dengan geometri analitik. Ke -8. Edisi. Bukit McGraw.
3. Matematika adalah permainan. Garis dan sudut. Pulih dari: juntadadeandalucia.adalah.
4. Garis yang salib. Dipulihkan dari: Teacheraltuna.com.
5. Villena, m. Geometri analitik di R3. Diperoleh dari: dspace.Espol.Edu.Ec.