Baris kedua

Kayu pintu taman ini bersedia sedemikian rupa sehingga mereka menentukan garis kering. Sumber: f. Zapata. Pxhere.com

Apa saja garis kering?

Di pesawat, Baris kedua Mereka adalah mereka yang memotong garis dan kurva lain. Dalam kasus dua garis, persimpangannya adalah titik, sedangkan garis seksi pada kurva, memotongnya menjadi dua atau lebih titik.

Amati pagar sosok atas dengan hati -hati. Di atasnya telah ditarik beberapa warna lurus lurus, dilambangkan sebagai l₁, L₂ dan saya₃. Panah di kedua sisi berarti bahwa garis -garis tersebut berkepanjangan tanpa batas waktu.

Nah, garis l₁, L₂ dan saya₃ Mereka saling mengeringkan, karena masing -masing pasangannya dipotong pada titik -titik ungu.

Selain itu, garis l₁ dan saya₂, Seperti l₁ dan saya₃, Mereka menentukan 4 sudut satu sama lain, dua di antaranya akut dan tumpul lainnya, sedangkan garis l₂ dan saya₃ Mereka tegak lurus, yang berarti bahwa 4 sudut yang ditentukan oleh mereka lurus.

Dua garis paralel tidak akan pernah kering, karena, karena kondisinya, mereka tidak memiliki titik kebetulan. Pada gilirannya, garis -garis yang bertepatan tidak kering, karena mereka memiliki lebih dari satu titik yang sama.

Karakteristik garis pengeringan

• Dua garis penjahitan memiliki titik unik sebagai persimpangan.
• Lereng dua saluran pengeringan harus berbeda. Ya m₁ Itu adalah kemiringan garis l₁, dan m₂ Itu adalah kemiringan garis l₂, maka terpenuhi bahwa m₁ ≠ m₂.
• Lereng dari dua saluran pengeringan tegak lurus satu sama lain, yang lerengnya masing -masing adalah m₁ dan m₂, Mereka memenuhi hubungan m₁ = -1/ m₂. Selain itu, produk skalar antara dua vektor v Dan atau terkandung dalam baris ini adalah nol, karena definisi produk skalar adalah v atau = v ∙ u ∙ cos θ, menjadi θ sudut antara vektor.
• Suatu garis dapat disesuaikan dengan kurva atau sosok geometris lainnya.
• Saat berpotongan, dua garis pengeringan menghasilkan 4 sudut, identik dua hingga dua atau identik satu sama lain.

Dapat melayani Anda: persamaan fraksional

Bagaimana mengetahui apakah dua garis kering

Dari karakteristik garis pengeringan yang dijelaskan di atas, dimungkinkan untuk menetapkan tiga kriteria untuk mengetahui apakah dua garis kering:

-Membandingkan lereng. Jika ini berbeda, garisnya kering.

-Melaksanakan produk skalar antara dua vektor yang terkandung dalam baris ini, disebut Sutradara. Jika produk skalar batal, garisnya kering dan tegak lurus, dan jika non -zero, dimungkinkan untuk mengetahui sudut minimum di antara mereka, yang merupakan sudut akut yang ada di antara garis -garis tersebut.

Asalkan sudut ini berbeda dari 0º, garis kering, dan jika sama dengan 0º, maka itu adalah garis paralel.

-Secara langsung menghitung sudut akut yang ada di antara garis -garis, diketahui lerengnya. Ini dapat dilakukan melalui formula yang menghubungkan garis singgung sudut tersebut dengan lereng.

Biarkan m₁ dan m₂ lereng, dan θ sudut akut di antara mereka. Singgung θ diberikan oleh:

Jenis Garis Pengeringan

Ketika dua garis saling mengering, mereka bisa menjadi tipe berikut:

• Miring, Jika saat dipotong mereka membentuk dua sudut akut dan dua sudut tumpul. Sudut -sudut ini adalah pelengkap, yaitu, jumlah ukuran sudut plus salah satu sudut tumpul sama dengan 180º. Secara total, jumlah dari 4 sudut sama dengan 360º.
• Tegak lurus, Mereka yang berpotongan 4 sudut yang sama dengan 90º.

Bagaimana menemukan persimpangan antara dua baris

Jika dua garis mengering, mereka hanya memiliki satu titik potong, yang memecahkan sistem dua persamaan linier dengan dua yang tidak diketahui. Jika garis diberikan secara umum: AX + oleh = C, sistem persamaan tersebut adalah:

Dapat melayani Anda: Set Infinite: Properti, Contoh

ke₁x + b₁ y = c₁

ke₂x + b₂ y = c₂

Cara menemukan persimpangan antara garis dan kurva

Mengetahui persamaan garis dan kurva, sistem persamaan diusulkan dan, yang solusinya sesuai dengan titik persimpangan. Jika sistem tidak memiliki solusi, garis tidak aman ke kurva, juga bukan jika ada titik pemotongan tunggal, karena, dalam hal ini, garis itu bersinggungan dengan kurva.

Agar garis dikeringkan, sebagaimana dinyatakan di awal, sistem persamaan harus memiliki dua atau lebih solusi.

Contoh Garis Pengeringan

Pesawat Cartesian

Pesawat Cartesian ditentukan oleh dua baris, disebut Sumbu x Dan Sumbu y, masing -masing horizontal dan vertikal. Garis -garis ini tegak lurus dan titik persimpangannya disebut Asal sistem koordinat, atau sekadar asal.

Diagonal poligon

Poligon adalah sosok datar dari tiga sisi atau lebih, yang bergabung dalam titik yang disebut simpul. Segmen yang bergabung dengan dua simpul non -berturut -turut adalah diagonal dari poligon, dan garis yang mengandung segmen tersebut adalah bagian poligon yang dimaksud.

Tali keliling

Tali keliling adalah segmen yang bergabung dengan dua poinnya. Tali utama adalah diameter, yang selalu melewati pusat keliling. Nah, garis yang berisi tali apa pun, termasuk diameternya, adalah garis pengeringan ke lingkar.

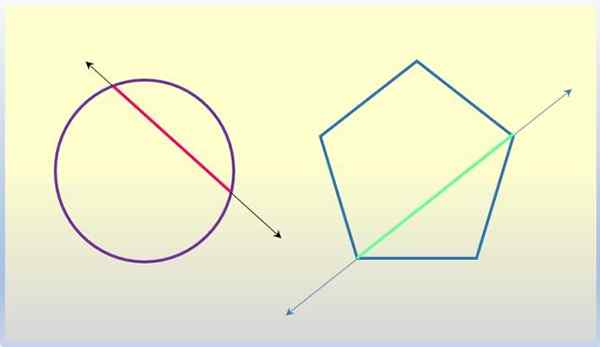Baris kedua untuk angka geometris. Sumber: f. Zapata.

Kunci salib

Dengan alat ini kacang yang menahan ban ke roda kendaraan longgar. Lengan membentuk garis yang kering dan pada saat yang sama tegak lurus.

Dapat melayani Anda: variasi proporsional

Lirik Alfabet

Beberapa huruf alfabet terdiri dari sapuan lurus yang menentukan secant. Misalnya, huruf X terdiri dari dua pukulan yang dipotong dalam satu titik dan huruf t terdiri dari dua garis tegak lurus.

Latihan terpecahkan

Latihan 1

Tentukan apakah garis yang diberikan oleh:

L₁ : y = 5x - 3

L₂ : y = -2x+1

Larutan

Kemiringan garis yang diberikan dalam bentuk y = mx + b adalah nilai m, yaitu koefisien yang menyertai x. Sejak m₁ = 5 dan m₂ = -2, yang berbeda, disimpulkan bahwa garisnya kering.

Latihan 2

Apa sudut akut antara garis Latihan 1?

Larutan

Nilai M secara langsung diganti₁ = 5 dan m₂ = -2 dalam formula yang diberikan di bagian sebelumnya:

Oleh karena itu, sudut antara garis adalah θ = arctg 0.777… = 37.9º.

Latihan 3

Apa persimpangan antara garis latihan sebelumnya?

Larutan

Sistem persamaan diusulkan sebagai berikut:

Yang solusinya adalah: x = 4/7; y = -1/7 (dapat diselesaikan dengan salah satu metode resolusi untuk sistem persamaan, atau dengan kalkulator).

Oleh karena itu, titik persimpangan garis adalah: p (4/7; -1/7).

Referensi

1. Geometri analitik.Info. Baris kedua. Pulih dari: geometriaanalitik.Info.
2. Larson, r. 2006. Perhitungan dengan geometri analitik. Ke -8. Edisi. Bukit McGraw.
3. Garis yang salib. Dipulihkan dari: Teacheraltuna.com.
4. Requena, b. Baris kedua. Pulih dari: universoformulas.com.
5. Villena, m. Geometri analitik di R3. Diperoleh dari: dspace.Espol.Edu.Ec.