Pengurangan istilah yang sama

Apa pengurangan istilah yang sama?

Itu Pengurangan istilah yang sama Ini adalah metode yang digunakan untuk menyederhanakan ekspresi aljabar. Dalam ekspresi aljabar, istilah yang sama adalah yang memiliki variabel yang sama; yaitu, mereka memiliki yang tidak diketahui yang sama diwakili oleh surat, dan mereka memiliki eksponen yang sama.

Dalam beberapa kasus polinomial luas, dan untuk mencapai solusi, Anda harus mencoba mengurangi ekspresi; Itu mungkin ketika ada istilah yang serupa, yang dapat dikombinasikan dengan menerapkan operasi dan sifat aljabar seperti jumlah, pengurangan, perkalian dan pembagian dan pembagian.

Penjelasan

Istilah yang sama dibentuk oleh variabel yang sama dengan eksponen yang sama, dan dalam beberapa kasus ini hanya berbeda dengan koefisien numeriknya.

Mereka yang tidak memiliki variabel juga dianggap sebagai istilah yang sama; yaitu istilah -istilah yang hanya memiliki konstanta. Jadi, misalnya, berikut ini adalah istilah yang sama:

• 6x² - 3x². Kedua istilah memiliki variabel x yang sama².
• 4²B³ + 2nd²B³. Kedua istilah memiliki variabel yang sama²B³.
• 7 - 6. Persyaratannya konstan.

Istilah -istilah yang memiliki variabel yang sama, tetapi dengan eksponen yang berbeda disebut istilah yang tidak mudah, seperti:

• Ke -9²B + 5AB. Variabel memiliki eksponen yang berbeda.
• 5x + dan. Variabelnya berbeda.
• B - 8. Satu istilah memiliki variabel, yang lain adalah konstan.

Mengidentifikasi istilah serupa yang membentuk polinomial, ini dapat dikurangi menjadi satu, menggabungkan semua orang yang memiliki variabel yang sama dengan eksponen yang sama. Dengan cara ini, ekspresi disederhanakan dengan mengurangi jumlah istilah yang menyusunnya dan perhitungan solusinya difasilitasi.

Cara membuat pengurangan istilah yang sama?

Pengurangan istilah serupa dilakukan dengan menerapkan properti asosiatif dari penambahan dan properti distributif produk. Menggunakan prosedur berikut, pengurangan istilah dapat dilakukan:

• Pertama, istilah serupa dikelompokkan bersama.
• Koefisien (angka yang menyertai variabel) dari istilah yang sama ditambahkan atau dikurangi, dan sifat asosiatif, komutatif atau distributif diterapkan, karena kasusnya mungkin.
• Maka istilah baru yang diperoleh ditulis, menempatkan di depan mereka tanda yang dihasilkan dari operasi.

Dapat melayani Anda: matematika diskrit

Contoh

Kurangi ketentuan ekspresi berikut: 10x + 3y + 4x + 5y.

Larutan

Pertama persyaratan diperintahkan untuk mengelompokkan yang serupa, menerapkan properti komutatif:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Maka properti distributif diterapkan dan koefisien yang menyertai variabel ditambahkan untuk mendapatkan pengurangan ketentuan:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) dan

= 14x + 8y.

Untuk mengurangi istilah yang sama, penting untuk memperhitungkan tanda -tanda yang memiliki koefisien yang menyertai variabel. Ada tiga kasus yang mungkin:

Pengurangan istilah yang sama dengan tanda yang sama

Dalam hal ini koefisien ditambahkan dan di depan hasil tanda persyaratan ditempatkan. Oleh karena itu, jika mereka positif, persyaratan yang dihasilkan akan positif; Jika persyaratannya negatif, hasilnya akan memiliki tanda (-) disertai dengan variabel. Misalnya:

a) 22ab² + 12ab² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Pengurangan istilah serupa cPada tanda -tanda yang berbeda

Dalam hal ini koefisien dikurangi, dan di depan hasil tanda koefisien utama ditempatkan. Misalnya:

a) 15x²dan - 4x²dan + 6x²dan - 11x²Dan

= (15x²dan + 6x²Y) + ( - 4x²dan - 11x²Dan)

= 21x²Y + (-15x²Dan)

= 21x²dan - 15x²Dan

= 6x²Dan.

b) -5a³B + 3 a³B - 4A³b + a³B

= (3 a³b + a³b) + (-5a³B - 4A³B)

= 4a³B - 9a³B

= -5 a³B.

Dengan cara ini, untuk mengurangi istilah serupa yang memiliki tanda -tanda berbeda, istilah aditif tunggal dibentuk dengan semua yang memiliki tanda positif (+), koefisien ditambahkan dan hasilnya disertai dengan variabel.

Ini dapat melayani Anda: Lingkaran Kesatuan: Fungsi dan Aplikasi Trigonometri

Dengan cara yang sama istilah subtraktif terbentuk, dengan semua istilah yang memiliki tanda negatif (-), koefisien ditambahkan dan hasilnya disertai dengan variabel.

Akhirnya, jumlah dari dua istilah yang terbentuk dikurangi, dan tanda yang terbesar ditempatkan pada hasilnya.

Pengurangan istilah yang serupa dalam operasi

Pengurangan istilah yang sama adalah operasi aljabar, yang dapat diterapkan dalam jumlah, pengurangan, perkalian dan divisi aljabar.

Dalam jumlah

Ketika Anda memiliki beberapa polinomial dengan istilah yang sama, untuk menguranginya, ketentuan masing -masing polinomial diperintahkan menjaga tanda -tanda mereka, maka mereka ditulis setelah yang lain dan istilah yang sama dikurangi. Misalnya, Anda memiliki polinomial berikut:

3x - 4xy + 7x²dan + 5xy².

- 6x²dan - 2xy + 9 xy² - 8x.

Dalam pengurangan

Untuk mengurangi polinomial dari yang lain, minuend ditulis dan kemudian mengurangi dengan tanda -tanda yang diubah, dan kemudian pengurangan istilah yang sama dilakukan. Misalnya:

Ke -5³ - 3ab² + 3b²C

6ab² + 2nd³ - 8b²C

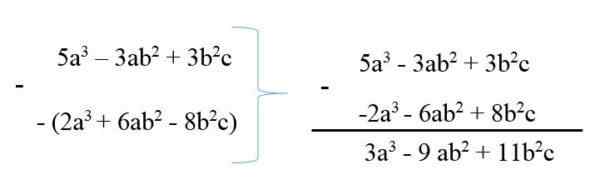
Dengan demikian, polinomial dirangkum pada 3a³ - 9ab² + 11b²C.

Dalam perkalian

Dalam produk polinomial, istilah yang membentuk pengalikan untuk setiap istilah yang membentuk pengganda, mengingat bahwa tanda -tanda perkalian tetap sama jika ini positif jika mereka positif.

Mereka hanya akan diubah ketika dikalikan dengan istilah yang negatif; Yaitu, ketika dua istilah dari tanda yang sama melipatgandakan hasilnya akan positif (+), dan ketika mereka memiliki tanda yang berbeda, hasilnya akan negatif (-).

Misalnya:

a) (a + b) _* (A + B)

= a² + Ab + ab + b²

= a² + 2ab+ b².

b) (a + b) _* (A - b)

= a² - Ab + ab - b²

= a² - B².

taksi) _* (A - b)

= a² - AB - AB + B²

= a² - 2ab+ b².

Di divisi

Ketika Anda ingin mengurangi dua polinomial melalui divisi, polinomial ketiga harus.

Itu dapat melayani Anda: Tukey Test: Apa yang, dalam kasus contoh, latihan terpecahkan

Untuk itu, ketentuan dividen dan pembagi harus dipesan, dari kiri ke kanan, sehingga variabel dalam keduanya berada dalam urutan yang sama.

Divisi ini kemudian dilakukan, mulai dari istilah pertama kiri dividen antara yang pertama di sebelah kiri pembagi, selalu mempertimbangkan tanda -tanda setiap istilah.

Misalnya, kurangi polinomial: 10x⁴ - 48x³dan + 51x²Dan² + 4xy³ - 15y⁴ membaginya antara polinomial: -5x² + 4xy + 3y².

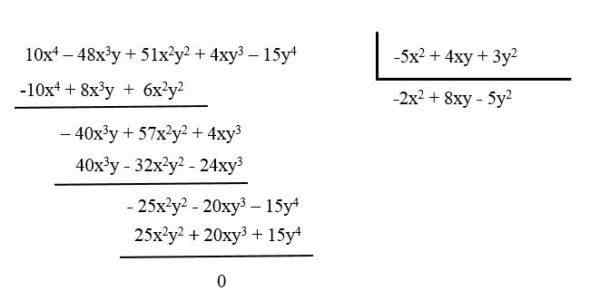
Polinomial yang dihasilkan adalah -2x² + 8xy - 5y².

Latihan terpecahkan

Latihan Pertama

Kurangi ketentuan ekspresi aljabar yang diberikan:

15a² - 8ab + 6a² - 6ab - 9 +4a² - 13 AB.

Larutan

Properti komutatif dari jumlah tersebut diterapkan, mengelompokkan persyaratan yang memiliki variabel yang sama:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15a² + 6² + 4²) + ( - 8ab - 6ab) + (9 - 13).

Kemudian properti distributif dari perkalian diterapkan:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Akhirnya, mereka disederhanakan dengan menambahkan dan mengurangi koefisien setiap istilah:

15a² - 8ab + 6a² - 6ab + 9 + 4a² - 13

= 25a² - 14AB - 4.

Latihan kedua

Sederhanakan produk dari polinomial berikut:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Larutan

Setiap istilah polinomial pertama dikalikan dengan yang kedua, dengan mempertimbangkan bahwa tanda -tanda persyaratan berbeda; Oleh karena itu, hasil perkaliannya akan negatif, serta hukum eksponen harus diterapkan.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²Dan⁴

= 64 x⁶ - 49 x²Dan⁴.