Vektor Grafis Subs

Itu Pengurangan vektor o Pengurangan vektor antar vektor atau Dan v dilambangkan oleh atau - v, Itu dihitung dengan menambahkan vektor atau dengan vektor yang berlawanan v. Aljabar pengurangan dinyatakan sebagai berikut:

atau - v = atau + (-v)

Dimungkinkan untuk melakukan pengurangan vektor yang mengikuti berbagai prosedur, misalnya dalam bentuk grafik, dengan cara ini vektor v Itu ditarik oleh segmen garis berorientasi -panah-.

Panjang panah sesuai dengan modul vektor, kecenderungan - mengenai garis referensi yang diberikan - menunjukkan arah dan ujungnya menunjukkan arah vektor.

Vektor yang menentang v Itu memiliki panjang dan arah yang sama, tetapi sebaliknya. Kemudian, sebelum pengurangan antara atau Dan v, Perlu untuk menggambar vektor yang berlawanan v, dan tambahkan vektor ini ke u.

Sangat penting untuk menekankan bahwa pengurangan vektor tidak komutatif, yaitu, urutan vektor memang mengubah hasilnya, oleh karena itu: oleh karena itu:

atau - v ≠ v - atau

Prosedur grafis dapat dilakukan dengan menggunakan salah satu metode ini, yang langkahnya akan kami jelaskan di bawah ini:

-Metode segitiga.

-Metode jajaran genjang.

[TOC]

Metode Sub -Grafik Vektor

Metode segitiga

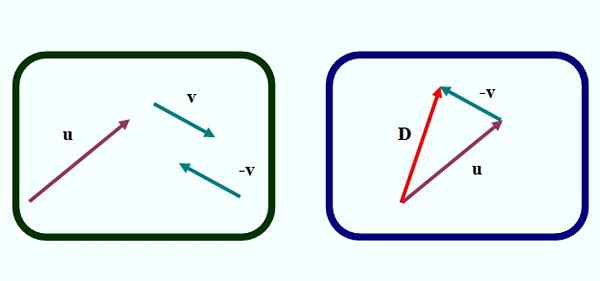
Gambar 1. Vektor Survance Menurut metode segitiga. Sumber: f. Zapata.

Pada Gambar 1 kita memiliki metode pertama untuk mengurangi dua vektor secara grafis. Ini tentang Metode segitiga, Karena gambar yang terbentuk saat membangun vektor adalah segitiga, seperti yang bisa kita lihat di gambar kiri.

Untuk mengurangi atau - v Kami melanjutkan sebagai berikut:

-Gambar vektor -v Dari vektor v, dengan terjemahan dengan aturan dan pasukan, tetapi mengubah arah panah (gambar kiri).

-Pindah ke vektor -v sedemikian rupa sehingga asalnya bertepatan dengan akhir vektor atau (gambar kanan).

Dapat melayani Anda: gesekan: jenis, koefisien, perhitungan, latihan

-Vektor kemudian ditarik (merah di gambar kanan) yang berasal dari asal atau sampai akhir v. Panggilan D Dan itu adalah perbedaan vektor:

D = atau - v

Metode jajaran genjang

Dalam metode jajaran genjang, vektor untuk menambah atau mengurangi harus bertepatan di titik asalnya. Misalkan kita ingin menemukan atau - v Dengan vektor kami yang ditunjukkan di atas, langkah -langkah untuk menemukan pengurangan vektor dengan metode ini adalah sebagai berikut:

-Tentukan vektor yang berlawanan v, apa -v, Seperti yang dijelaskan sebelumnya untuk metode segitiga.

-Ambil vektor dengan cermat atau Dan -v sedemikian rupa sehingga asal -usulnya bertepatan.

-Sekarang garis paralel tersegmentasi diambil dari ujung masing -masing vektor. Angka yang terbentuk adalah jajaran genjang dan dalam kasus -kasus khusus di mana vektor tegak lurus, itu adalah persegi panjang atau persegi.

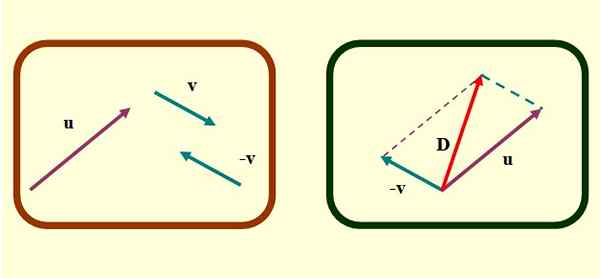Gambar 2. Metode jajaran genjang untuk pengurangan vektor. Sumber: f. Zapata.

-Akhirnya, vektor yang dimulai dari asal usul yang umum atau Dan v Di ujung di mana garis paralel tersegmentasi dilintasi. Ini adalah vektor D atau pengurangan.

Penting

Cara lain untuk melakukan pengurangan adalah dengan menggambar jajaran genjang seolah -olah Anda ingin menambahkan vektor.

Tetapi alih -alih menggambar diagonal jumlah yang biasa, yang beralih dari asal umum ke persimpangan paralel, Diagonal berlawanan atau lebih pendek, seperti yang terlihat pada gambar:

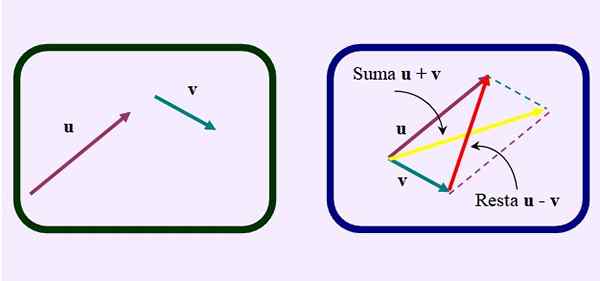Gambar 3. Cara lain untuk melakukan pengurangan vektor melalui metode jajaran genjang. Sumber: f. Zapata.

Contoh pengurangan vektor

- Contoh 1

Sebuah kapal menavigasi di sungai dan melakukannya ke arah yang berlawanan dari arus. Seorang pengamat di darat mengamati bahwa kecepatan kapal berkurang karena aksi arus.

Dapat melayani Anda: bagaimana dengan energi yang terkandung dalam material?

Kecepatan adalah vektor dan dalam contoh ini, kecepatan kapal menunjuk dalam satu arah dan arus memiliki arah yang sama dan arah yang berlawanan. Kecepatan bersih kapal adalah jumlah dari kedua vektor.

Misalnya, jika instrumen kapal. Sebagai v = v ' +vc, menjadi vc kecepatan arus yang dihitung dengan pengurangan kecepatan v dan v' masing -masing: vc = v - v '= 30 km/jam - 40 km/jam = -10 km/ H.

- Contoh 2

Dalam sinematik kami memiliki vektor penting yang menggambarkan perubahan:

-Perpindahan untuk perubahan posisi.

-Kecepatan rata -rata, untuk mengukur seberapa cepat posisi bervariasi dalam waktu.

-Percepatan, untuk modifikasi kecepatan sebagai fungsi waktu.

Vektor perpindahan

Vektor perpindahan menggambarkan perubahan posisi yang dialami tubuh dalam perjalanan gerakannya.

Mari kita lihat misalnya sebuah partikel yang menggambarkan lintasan datar yang ditunjukkan pada gambar, di mana ia pergi dari titik p₁ ke titik p₂.

Vektor yang diarahkan dari asal sistem koordinat x-y ke titik-titik ini adalah vektor posisi R₁ Dan R₂, Sedangkan vektor perpindahan adalah ΔR, mulai dari hal₁ A p₂. Memang benar bahwa:

ΔR = R₂ - R₁

Oleh karena itu, vektor perpindahan adalah pengurangan antara vektor posisi akhir dan vektor posisi awal, sebagaimana dicatat oleh gambar berikut. Unit -unitnya juga dari posisi: meter, kaki, mil, sentimeter dan banyak lagi.

Dapat melayani Anda: Perseus (Constellation): Lokasi, Mitologi dan Karakteristik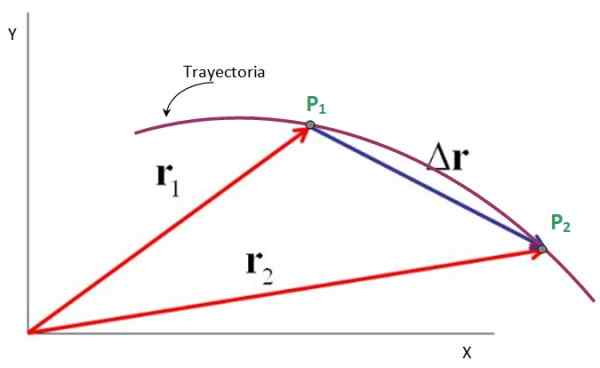Gambar 4. Vektor perpindahan adalah perbedaan antara posisi final dan awal. Sumber: f. Zapata.

Kecepatan rata -rata dan vektor akselerasi rata -rata

Untuk bagiannya, vektor kecepatan rata -rata v_M Ini didefinisikan sebagai perpindahan yang dikalikan dengan kebalikan dari interval waktu:

 Dan akselerasi rata -rata adalah:

Olahraga diselesaikan

Sebuah partikel yang menggambarkan lingkaran membutuhkan waktu 5 detik untuk lulus dari titik A ke titik B. Dalam A memiliki kecepatan v_KE = 60 km/jam menuju sumbu +x dan b v_B = 60 km/jam menuju +dan. Tentukan akselerasi rata -rata dalam bentuk grafik dan analitik.

Larutan

Dalam grafik, arah dan makna akselerasi rata -rata ditentukan oleh:

Pada gambar berikut adalah pengurangan v_B - v_KE, melalui metode segitiga, karena akselerasi rata -rata ke_M sebanding dengan δv. Segitiga yang dibentuk memiliki dua kategori yang sama dan oleh karena itu sudut internal akut masing -masing berukuran 45 º.

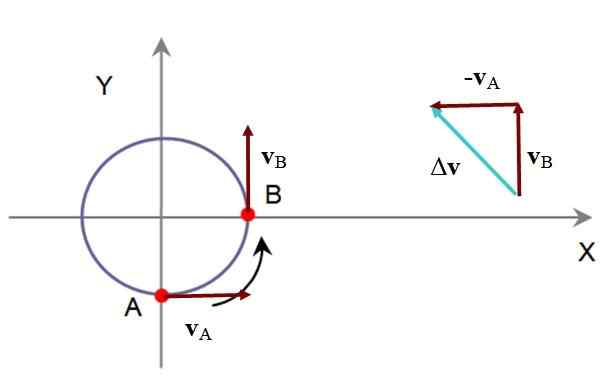Gambar 5. Diagram pergerakan partikel dari contoh terpecahkan. Sumber: f. Zapata.

Secara analitik, jika alamat +x bertepatan dengan vektor unit yo dan alamat +dan dengan vektor unit J, Jadi:

Δv = 60 km/jam J - 60 km/jam yo

Mengambil Δt = 5 detik, menurut informasi pernyataan, akselerasi rata -rata adalah:

ke_M = (60 km/jam J - 60 km/jam Yo) / 5 s = 12 (J-yo) Km/(h.S)

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
6. Tipler, hlm. 2006. Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan.