Setengah lingkaran cara menghitung perimeter, area, centroid, latihan

Dia setengah lingkaran Ini adalah sosok datar yang dibatasi oleh diameter lingkar dan salah satu dari dua lengkungan melingkar datar yang ditentukan oleh diameter tersebut.

Dengan cara ini, setengah lingkaran dibatasi oleh a semisircumference, yang terdiri dari busur melingkar datar dan segmen lurus yang bergabung dengan ujung busur melingkar datar. Setengah lingkaran mencakup setengah lingkaran dan semua titik interior yang sama.

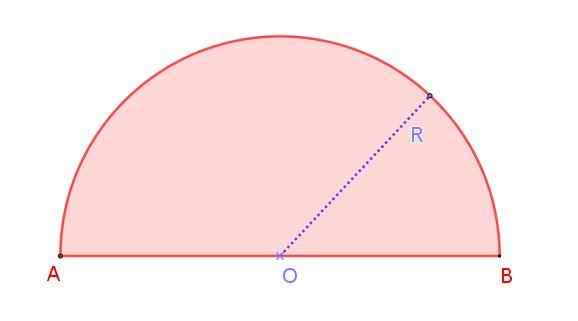Gambar 1. Radio R Radio setengah lingkaran. Sumber: f. Zapata.

Kita dapat melihat ini pada Gambar 1, yang menunjukkan radio r, yang ukurannya setengah dari diameter ab. Perhatikan bahwa tidak seperti lingkaran, di mana ada diameter tak terbatas, dalam setengah lingkaran hanya ada satu diameter.

Setengah lingkaran adalah sosok geometris dengan banyak kegunaan dalam arsitektur dan desain, seperti yang kita lihat pada gambar berikut:

Gambar 2. Seminicírculo sebagai elemen dekoratif dalam arsitektur. Sumber: Pikist.

[TOC]

Elemen dan ukuran setengah lingkaran

Elemen setengah lingkaran adalah:

1.- Busur melingkar datar a⌒b

2.- Segmen [ab] 

3.- Interior menunjuk setengah lingkaran yang terdiri dari busur dan segmen A⌒B [AB].

Perimeter setengah lingkaran

Perimeter adalah jumlah dari kontur lengkungan ditambah dengan segmen lurus, oleh karena itu: oleh karena itu:

Perimeter = Panjang busur A⌒B + Panjang Segmen [AB]

Dalam kasus setengah lingkaran radio r perimeternya p akan diberikan oleh formula:

P = π⋅r + 2⋅r = (π + 2) ⋅R

Istilah pertama adalah setengah dari perimeter lingkar jari -jari R, sedangkan yang kedua adalah panjang diameter, yang dua kali jari -jari.

Dapat melayani Anda: skala termometrik

Area setengah lingkaran

Sebagai setengah lingkaran adalah salah satu sektor sudut datar yang tetap dengan menarik diameter melalui lingkar, area A akan menjadi setengah dari area lingkaran yang berisi setengah lingkaran radio R:

A = (π⋅r²) / 2 = ½ π⋅r²

Centroid dari setengah lingkaran

Centroid dari setengah lingkaran berada pada sumbu simetri ke ketinggian yang diukur dari diameter 4/(3π) kali jari -jari R.

Ini sesuai dengan sekitar 0,424⋅R, diukur dari pusat setengah lingkaran dan pada sumbu simetri, seperti yang ditunjukkan pada Gambar 3.

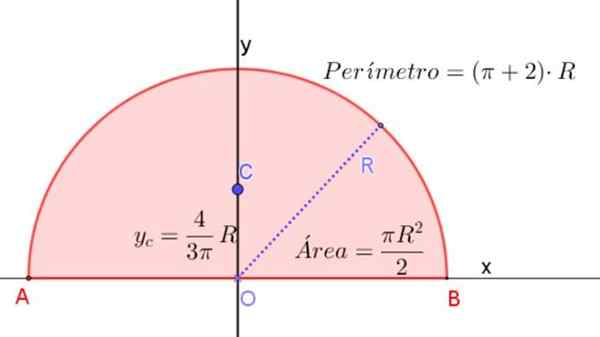Gambar 3. Setengah lingkaran radio r, menunjukkan formula untuk menentukan area, perimeter, dan lokasi centroidnya. Sumber: f. Zapata.

Momen inersia setengah lingkaran

Momen inersia dari sosok datar didefinisikan sehubungan dengan sumbu, misalnya sumbu x, seperti:

Integral kuadrat dari jarak titik -titik yang dimiliki oleh gambar ke sumbu, diferensial integrasi menjadi area yang sangat kecil, diambil dalam posisi setiap titik. 

Gambar 4 menunjukkan definisi momen inersia i_X dari setengah lingkaran radio R, sehubungan dengan sumbu X yang melewati diagonalnya:

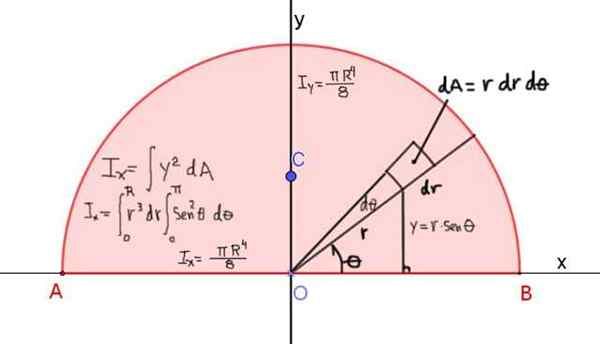Gambar 4. Definisi momen inersia IX dari setengah lingkaran sehubungan dengan sumbu x yang melewati diagonalnya. Hasilnya ditunjukkan untuk saat -saat inersia sehubungan dengan sumbu x dan y. Sumber: f. Zapata.

Momen inersia sehubungan dengan sumbu x diberikan oleh:

yo_X = (π⋅r⁴) / 8

Dan momen inersia sehubungan dengan sumbu simetri dan adalah:

Dapat melayani Anda: optik bergelombang

Iy = (π⋅r⁴) / 8

Ini menunjukkan bahwa kedua momen inersia bertepatan dalam formula mereka, tetapi penting untuk menekankan bahwa mereka dirujuk ke sumbu yang berbeda.

Sudut terdaftar

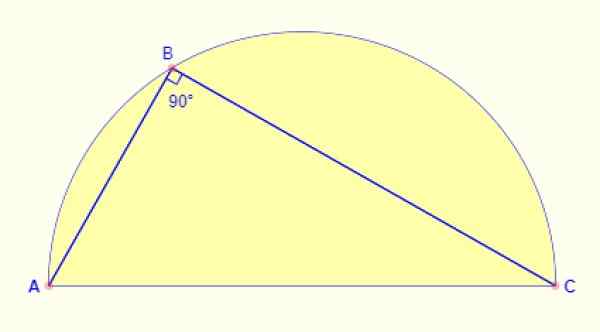
Sudut yang terdaftar dalam setengah lingkaran selalu 90º. Terlepas dari bagian lengkungan mana yang diambil ke titik, sudut yang terbentuk di antara sisi AB dan BC dari gambar selalu lurus.

Gambar 5. Sudut terdaftar di setengah lingkaran. Sumber: Referensi Terbuka Matematika.

Latihan terpecahkan

Latihan 1 

Tentukan perimeter setengah lingkaran radius 10 cm.

Larutan

Ingatlah bahwa perimeter tergantung pada jari -jari diberikan oleh rumus yang kita lihat sebelumnya:

P = (2 + π) ⋅R

P = (2 + 3.14) ⋅ 10 cm = 5.14 ⋅ 10 cm = 51.4 cm.

Latihan 2

Temukan area setengah lingkaran radio 10 cm.

Larutan

Formula untuk area setengah lingkaran adalah:

A = ½ π⋅r² = ½ π⋅ (10cm)² = 50π cm² = 50 x 3,14 cm² = 157 cm².

Latihan 3

Tentukan tinggi h dari centroid dari setengah lingkaran radius R = 10 cm diukur dari pangkalannya, yang sama adalah diameter setengah lingkaran. 

Larutan

Centroid adalah titik kesetimbangan setengah lingkaran dan posisinya berada pada sumbu simetri pada ketinggian h pangkalan (diameter setengah lingkaran):

H = (4⋅r) / (3π) = (4⋅10 cm) / (3 x 3.14) = 4.246 cm

Latihan 4

Temukan momen inersia dari setengah lingkaran sehubungan dengan sumbu yang bertepatan dengan diameternya, mengetahui bahwa setengah lingkaran terbuat dari lembaran tipis. Radiusnya adalah 10 cm dan massanya 100 gram.

Larutan

Formula yang memberikan momen inersia dari setengah lingkaran adalah:

Dapat melayani Anda: fisika keadaan padat: sifat, struktur, contoh

yo_X = (π⋅r⁴) / 8

Tetapi seperti yang dikatakan masalah kepada kita bahwa itu adalah setengah lingkaran material, maka hubungan sebelumnya harus dikalikan dengan kepadatan permukaan massa setengah lingkaran, yang akan dilambangkan dengan σ.

yo_X = σ (π⋅r⁴) / 8

Kami kemudian menentukan σ, yang tidak lain adalah massa setengah lingkaran yang dibagi antara area yang sama.

Area tersebut ditentukan dalam Latihan 2 dan hasilnya adalah 157 cm². Maka kepadatan superfisial dari setengah lingkaran ini adalah:

σ = 100 gram / 157 cm² = 0,637 g/cm²

Kemudian momen inersia sehubungan dengan diameter akan dihitung sebagai berikut:

yo_X = (0,637 g/cm²) [3.1416 ⋅ (10cm)⁴]/ 8

Yang dihasilkan:

yo_X = 2502 g⋅cm²

Latihan 5

Tentukan momen inersia radius setengah lingkaran 10 cm yang dibangun dari lembar material dengan kepadatan permukaan 0,637 g/cm² dengan sumbu yang melewati centroid dan sejajar dengan diameternya.

Larutan

Untuk menyelesaikan latihan ini, perlu untuk mengingat teorema Steiner pada saat -saat inersia sumbu paralel, yang mengatakan:

Momen inersia I sehubungan dengan sumbu yang berada pada jarak h dari centroid sama dengan jumlah momen inersia i_C Mengenai sumbu yang melewati centroid dan sejajar dengan yang pertama lagi produk adonan melalui kuadrat pemisahan dua sumbu.

I = i_C + M h²

Dalam kasus kami, diketahui bahwa itu adalah momen inersia sehubungan dengan diameter, yang sudah dihitung dalam Latihan 4. H juga tahu antara diameter dan centroid, yang dihitung dalam Latihan 3.

Kami hanya perlu menghapus IC:

yo_C = I - m h²

yo_C = 2502 g⋅cm² - 100g ⋅ (4.246 cm)² mengakibatkan momen inersia oleh sumbu yang sejajar dengan diameter dan melewati centroid adalah: 

yo_C = 699.15 g⋅cm²

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Referensi Terbuka Matematika. Setengah lingkaran. Pulih dari: mathpenref.com.
3. Rumus alam semesta.Setengah lingkaran. Pulih dari: universoformulas.com.
4. Rumus alam semesta. Area setengah lingkaran. Pulih dari: universoformulas.com.
5. Wikipedia. Setengah lingkaran. Diperoleh dari: di.Wikipedia.com.