Sistem Solusi Persamaan Metode, contoh, latihan

Itu Sistem Ekisiasi Mereka terdiri dari dua atau lebih persamaan dengan beberapa variabel yang harus memiliki solusi umum. Mereka sering, karena dalam praktiknya ada banyak situasi yang bergantung pada banyak faktor, yang terkait dalam beberapa cara.

Secara umum, sistem persamaan memiliki bentuk berikut, di mana setiap fungsi mewakili salah satu kondisi yang harus dipenuhi solusi:

Gambar 1. Sistem persamaan terdiri dari fungsi M dan tidak diketahui. Sumber: f. Zapata.

Mari kita lihat contoh: Misalkan Anda perlu memproduksi lembar kertas persegi panjang yang luasnya 180 cm² dan memiliki perimeter 54 cm. Apa yang seharusnya menjadi dimensi lembar?

Untuk menjawab pertanyaan yang kami pertimbangkan bahwa dimensi lembaran persegi panjang adalah dua: lebar dan tinggi. Ini berarti bahwa kami memiliki 2 variabel yang akan kami berikan nama biasa X Dan Dan.

Dan variabel -variabel ini harus memenuhi dua kondisi yang dikenakan pada saat yang sama:

-Kondisi Pertama: Area Lamina adalah 180 cm². Ini akan menjadi fungsi pertama: f₁.

-Kondisi kedua: Perimeter atau kontur lembaran harus 54 cm. Ini adalah fungsi F kedua₂.

Untuk setiap kondisi, persamaan ditetapkan menggunakan bahasa aljabar. Area A dari lembaran persegi panjang diperoleh dengan mengalikan lebar:

A = x.y = 180 cm²

Dan perimeter P hasil dari menambahkan sisi. Karena perimeter adalah jumlah sisi:

P = 2x + 2y = 54 cm

Sistem yang dihasilkan dari dua persamaan dan dua tidak diketahui adalah:

Xy = 180

2 (x + y) = 54

Kami membutuhkan dua angka yang produknya 180 dan bahwa produk ganda dari jumlahnya adalah 54, atau apa yang sama: ditambahkan harus memberikan 27. Angka -angka ini adalah 12 dan 15.

Di bagian Latihan Terselesaikan kami akan menawarkan metode terperinci untuk menemukan nilai -nilai ini, sementara pembaca dapat dengan mudah memverifikasi penggantian, yang secara efektif memenuhi kedua persamaan.

[TOC]

Contoh aplikasi sistem persamaan

Situasi yang diusulkan di atas berisi 2 variabel, dan setidaknya 2 persamaan diperlukan untuk menemukannya. Ada sistem dengan lebih banyak variabel, tetapi dalam hal apa pun, jika sistemnya N Dari ini, setidaknya diperlukan N Persamaan independen (seseorang tidak bisa menjadi kombinasi linier dari yang lain) untuk menemukan solusinya, jika ada.

Dapat melayani Anda: tali (geometri): panjang, teorema dan latihan

Adapun aplikasi, mereka banyak. Berikut adalah beberapa di mana sistem persamaan menunjukkan kegunaannya:

-Temukan arus yang beredar melalui sirkuit melalui hukum Kirchoff.

-Dalam transportasi darat dan udara untuk menetapkan jadwal keluar dan kedatangan.

-Temukan magnitudo gaya dalam sistem dinamis atau statis yang mengalami banyak interaksi.

-Untuk mengetahui jumlah barang yang dijual untuk jangka waktu tertentu, atau di pabrik, untuk menentukan dimensi objek untuk memenuhi kondisi tertentu dalam hal permukaan atau volume.

-Saat menentukan cara mendistribusikan modal dalam beberapa investasi.

-Menetapkan tarif untuk berbagai layanan, misalnya telekomunikasi atau menunjukkan dan mengetahui jumlah uang yang dikumpulkan (lihat contoh diselesaikan 2)

Metode Solusi Sistem Persamaan

metode penggantian

-Persamaan dipilih dan salah satu variabel dibersihkan.

-Maka Anda harus mengganti variabel yang jelas dalam persamaan lain. Maka variabel ini menghilang dari sana dan jika sistem memiliki dua persamaan dan dua yang tidak diketahui, ada persamaan dengan variabel yang sudah bisa jelas.

-Jika sistem memiliki lebih dari dua variabel, Anda harus menghapus yang ketiga tidak diketahui dari persamaan lain dan menggantinya juga.

Contoh penerapan metode ini adalah tahun yang diselesaikan 1.

Metode pengurangan atau eliminasi

Metode ini terdiri dalam menambahkan atau mengurangi persamaan untuk menghilangkan satu atau lebih variabel dan meninggalkan satu. Untuk melakukan ini, lebih mudah untuk melipatgandakan persamaan dengan faktor sehingga dengan menambahkan dengan persamaan lain, yang tidak diketahui menghilang. Mari kita lihat contoh:

3x² - Dan² = 11

Dapat melayani Anda: Tindakan Kecenderungan Pusat untuk Data Pengelompokan: Rumus, Latihan

X² + 4y² = 8

Kami melipatgandakan persamaan pertama dengan 4:

12x² - 4y² = 44

X² + 4y² = 8

Dengan menambahkan mereka, hal yang tidak diketahui menghilang Dan, tetap:

13x² = 52

X² = 4

Oleh karena itu x₁ = 2 dan x₂ = -2. Dengan nilai -nilai ini, pembaca dapat memverifikasi itu dan₁ = 1 dan₂ = -1

Metode penyetaraan

Ketika sistem adalah dua persamaan dengan dua tidak diketahui:

-Yang tidak diketahui dipilih dan jelas dari kedua persamaan.

-Hasilnya disamakan, yang memungkinkan untuk mendapatkan persamaan tunggal dengan satu yang tidak diketahui.

-Persamaan ini diselesaikan dan hasilnya diganti dalam salah satu pembukaan sebelumnya untuk mendapatkan nilai yang tidak diketahui lainnya.

Metode ini akan diterapkan pada tahun ini diselesaikan 2 dari bagian berikut.

Metode grafis

Metode ini terdiri dari grafik kurva yang diwakili oleh masing -masing persamaan. Titik persimpangan adalah solusi sistem. Contoh berikut menunjukkan solusi grafis sistem:

X² + Dan ² = 1

2x + 4y = 0

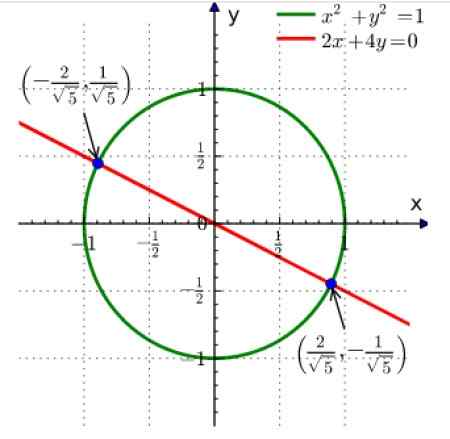Gambar 2. Solusi grafis dari sistem persamaan simultan adalah menemukan persimpangan kurva. Sumber: Wikimedia Commons.

Yang pertama dari persamaan adalah lingkaran jari -jari 1 yang difokuskan pada asal dan yang kedua adalah garis.

Persimpangan keduanya adalah dua titik yang ditampilkan dengan warna biru. Pembaca dapat memverifikasi bahwa dengan mengganti koordinat titik dalam persamaan di atas, kesetaraan diperoleh.

Latihan

- Latihan diselesaikan 1

Anda perlu memproduksi lembaran persegi panjang seluas 180 cm² dan dengan perimeter 54 cm. Apa yang seharusnya menjadi dimensi lembar?

Larutan

Sistem yang akan diselesaikan adalah:

Xy = 180

2 (x + y) = 54

Persamaan kedua dapat disederhanakan menjadi x + y = 27, oleh karena itu: oleh karena itu:

Xy = 180

x + y = 27

Salah satu yang tidak diketahui dari persamaan kedua dibersihkan:

y = 27 - x

Izin diganti pada yang pertama:

(27 -x) = 180

Menerapkan properti distributif:

-X² + 27x = 180

Mengalikan dengan (-1) di kedua sisi persamaan dan mengirim 180 ke sisi kiri:

X² - 27x +180 = 0

Ini adalah persamaan tingkat kedua dalam x, yang diselesaikan dengan rumus:

Itu dapat melayani Anda: sudut yang berlawanan dengan simpul (dengan latihan terselesaikan)

Dengan a = 1, b = -27 dan c = 180

 Solusinya adalah: x₁ = 15 cm dan x₂ = 12, oleh karena itu dimensi y adalah dan₁ = 12 cm dan dan dan₂ = 15 cm.

- Latihan diselesaikan 2

Taman hiburan memiliki tarif berikut per pintu masuk: Anak -anak 1.5 dan orang dewasa $ 4. Dalam satu hari ada 2.200 pengunjung, mengumpulkan $ 5050. Temukan jumlah anak dan orang dewasa yang mengunjungi taman hari itu.

Gambar 3. Sistem persamaan berfungsi untuk memecah koleksi taman hiburan dalam sehari. Sumber: Pixabay.

Larutan

Menjadi X Jumlah anak dan Dan Jumlah orang dewasa. Kita dapat menetapkan persamaan pertama yang mengetahui bahwa jumlah keduanya harus 2200:

x + y = 2200.

Sekarang kita pergi dengan uang yang dikumpulkan. Harga tiket untuk anak -anak adalah 1.5 $ untuk setiap anak, dengan mengalikan nilai ini dengan x, jumlah anak, kami akan memiliki jumlah untuk masuk anak:

1.5x = uang yang dikumpulkan oleh tiket anak -anak

Dan jika kita mengalikan $ 4 per orang dewasa untuk jumlah dan pengunjung dewasa, total uang diperoleh oleh semua orang dewasa:

4y = uang yang dikumpulkan oleh tiket dewasa

Kami menambahkan ini untuk mendapatkan $ 5050:

1.5x + 4y = 5050

Sistem persamaan kami adalah:

x + y = 2200

1.5x + 4y = 5050

Mari kita selesaikan dengan pemerataan. Kami menghapus variabel dan persamaan pertama dan kedua:

y = 2200 - x

y = (5050 - 1.5 x) /4

Kami sama dengan kedua ekspresi:

2200 - x = (5050 - 1.5x) /4

Kami melipatgandakan semuanya dengan 4 untuk menghilangkan fraksi:

8800 - 4x = 5050 - 1.5x

Kami mengelompokkan istilah dengan X di sebelah kiri dan angka murni di sebelah kanan:

-4x + 1.5x = 5050 - 8800

-2.5x = -3750

x = 1500 anak.

Kami mengganti nilai ini pada y = 2200 - x untuk mengetahui jumlah orang dewasa:

y = 2200 - 1500 = 700 orang dewasa.

Referensi

1. CK-12. Sistem persamaan dan ketidaksetaraan. Dipulihkan dari: CK12.org.
2. Hoffman, J. Pemilihan masalah matematika. Volume 2.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.