Contoh Suksesi Kuadratik, Aturan dan Latihan Diselesaikan

Itu Suksesi kuadratik, Dalam istilah matematika, mereka terdiri dari urutan angka yang mengikuti aturan aritmatika tertentu. Sangat menarik untuk mengetahui aturan ini untuk menentukan ketentuan suatu suksesi.

Salah satu cara untuk mencapai ini adalah dengan menentukan perbedaan antara dua istilah berturut -turut dan melihat apakah nilai yang diperoleh selalu diulangi. Ketika demikian, dikatakan bahwa itu adalah a suksesi reguler.

Succecsied Numerical adalah cara mengatur urutan angka. Sumber: Pixabay.com

Tetapi jika tidak diulang, maka Anda dapat mencoba memeriksa perbedaan antara perbedaan Dan lihat apakah nilai ini konstan. Jika demikian, maka itu adalah a Suksesi kuadratik. 

[TOC]

Contoh suksesi reguler dan suksesi kuadratik

Contoh -contoh berikut membantu memperjelas apa yang telah dijelaskan sejauh ini:

Contoh suksesi reguler

Jadilah suksesi s = 4, 7, 10, 13, 16, ...

Suksesi ini, dilambangkan dengan S, adalah set numerik yang tak terbatas, dalam hal ini dari bilangan bulat ini.

Dapat dilihat bahwa itu adalah suksesi biasa, karena setiap istilah diperoleh dengan menambahkan 3 ke istilah atau elemen sebelumnya:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Dengan kata lain: suksesi ini teratur karena perbedaan antara istilah berikut dan yang sebelumnya memberikan nilai tetap. Dalam contoh yang diberikan nilai ini adalah 3.

Suksesi reguler yang diperoleh dengan menambahkan jumlah tetap ke istilah sebelumnya, juga disebut Kemajuan aritmatika. Dan perbedaan - konstan - di antara istilah berturut -turut disebut alasan Dan itu dilambangkan sebagai r.

Contoh suksesi non -reguler dan kuadratik

Lihat sekarang suksesi berikut:

S = 2, 6, 12, 20, 30, .. .

Ketika perbedaan berturut -turut dihitung, nilai -nilai berikut diperoleh:

Dapat melayani Anda: pilihan acak dengan atau tanpa penggantian

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Perbedaan mereka tidak konstan, sehingga dapat dikatakan bahwa itu adalah suksesi yang tidak teratur.

Namun, jika kita mempertimbangkan serangkaian perbedaan, ada suksesi lain, yang akan dilambangkan sebagai s_Dif:

S_Dif = 4, 6, 8, 10, .. .

Suksesi baru ini adalah a suksesi reguler, Karena setiap istilah diperoleh dengan menambahkan nilai tetap r = 2 ke yang sebelumnya. Itulah sebabnya kita dapat menegaskan bahwa S adalah Suksesi kuadratik.

Aturan umum untuk membangun suksesi kuadratik

Ada formula umum untuk membangun suksesi kuadratik:

T_N = A ∙ n² + B ∙ n +c

Dalam formula ini, t_N Itu adalah istilah N dari suksesi. A, B dan C adalah nilai tetap, sedangkan n bervariasi satu per satu, yaitu 1, 2, 3, 4, ..

Secara berturut -turut dari contoh sebelumnya a = 1, b = 1 dan c = 0. Dari sana, ini mengikuti formula yang menghasilkan semua persyaratan adalah: t_N = n² + N

Artinya:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_N = n² + N

Perbedaan antara dua istilah berturut -turut dari suksesi kuadratik

T_N+1 - T_N = [A ∙ (n+1)² + B ∙ (n + 1) + c] - [a ∙ n² + B ∙ n +c]

Mengembangkan ekspresi melalui produk yang luar biasa tetap:

T_N+1 - T_N = A ∙ n² + A ∙ 2 ∙ N + A + B ∙ N + B + C - A ∙ N² - B ∙ n - c

Dengan menyederhanakannya, Anda dapatkan:

T_N+1 - T_N = 2 ∙ A ∙ N + A + B

Ini adalah formula yang memberikan suksesi perbedaan_Dif yang bisa ditulis seperti ini:

Dif_N = A ∙ (2n+1)+b

Di mana jelas istilah berikut adalah 2 ∙ terkadang sebelumnya. Yaitu, alasan suksesi perbedaan s_Dif Es: r = 2 ∙ a.

Latihan terselesaikan dari suksesi kuadratik

Latihan 1

Jadilah suksesi s = 1, 3, 7, 13, 21,…. Tentukan Ya:

i) Ini biasa atau tidak

ii) adalah kuadratik atau tidak

iii) adalah kuadratik, suksesi perbedaan dan alasannya

Itu dapat melayani Anda: membatasi sifat (dengan contoh)

Jawaban

i) Mari kita menghitung perbedaan istilah berikut dan yang sebelumnya:

3-1 = 2

7-3 = 4

13-7 = 6

21-13 = 8

Kita dapat menegaskan bahwa suksesi s tidak teratur, karena perbedaan antara istilah berturut -turut tidak konstan.

ii) Suksesi perbedaan adalah secara teratur, karena perbedaan antara persyaratannya adalah nilai konstan 2. Oleh karena itu suksesi asli S adalah kuadratik.

iii) Kami telah menentukan bahwa S adalah kuadratik, suksesi perbedaannya adalah:

S_Dif = 2, 4, 6, 8, ... dan alasannya adalah r = 2.

Latihan 2

Jadilah suksesi s = 1, 3, 7, 13, 21,… dari contoh sebelumnya, di mana diverifikasi bahwa itu adalah kuadratik. Menentukan:

i) rumus yang menentukan istilah umum t_{N .}

ii) Verifikasi istilah ketiga dan kelima.

iii) nilai istilah kesepuluh.

Jawaban

i) Formula umum T_N adalah ∙ n² + B ∙ n +c. Maka diketahui nilai A, B dan C.

Suksesi perbedaan itu benar 2. Selain suksesi kuadratik alasan R adalah 2 ∙ A seperti yang ditunjukkan pada bagian sebelumnya.

R = 2 ∙ a = 2 yang menuntun kita untuk menyimpulkan bahwa a = 1.

Istilah pertama dari suksesi perbedaan s_Dif Itu 2 dan harus mematuhi ∙ (2n+1)+b, dengan n = 1 dan a = 1, yaitu:

2 = 1 ∙ (2 ∙ 1+1)+b

Kliring B diperoleh: b = -1

Kemudian istilah pertama s (n = 1) vale 1, yaitu: 1 = a ∙ 1² + B ∙ 1 + C. Seperti yang sudah kita ketahui bahwa a = 1 dan b = -1, menggantikan kita, kita ditinggalkan:

1 = 1 ∙ 1² + (-1) ∙ 1 +c

Kliring C diperoleh nilainya: C = 1.

Kesimpulan:

A = 1, b = -1 dan c = 1

Maka istilahnya adil_N = n² - N + 1

ii) istilah ketiga t₃ = 3² - 3 + 1 = 7 dan diverifikasi. Yang kelima t₅ = 5² - 5 + 1 = 21 yang juga diverifikasi.

iii) istilah kesepuluh adalah t₁₀ = 10² - 10 + 1 = 91.

Latihan 3

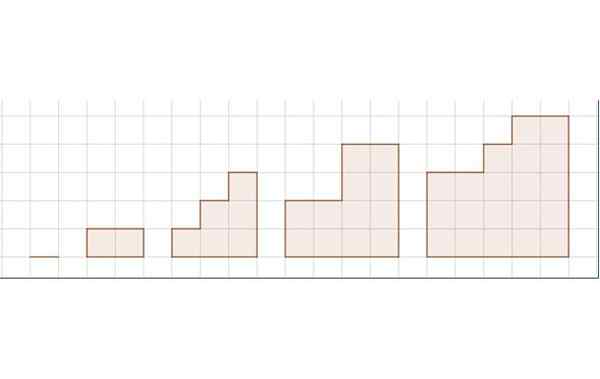Urutan Area untuk Latihan 3. Sumber: Made sendiri.

Gambar tersebut menunjukkan urutan lima angka. Retikulat mewakili satuan panjang.

Dapat melayani Anda: perbedaan antara fraksi umum dan angka desimal

i) Tentukan suksesi untuk area angka.

i) Tunjukkan bahwa itu adalah suksesi kuadratik.

iii) Temukan luas Gambar # 10 (tidak ditampilkan).

Jawaban

i) Suksesi yang sesuai dengan luas urutan angka adalah:

S = 0, 2, 6, 12, 20, ...

ii) Suksesi yang sesuai dengan perbedaan berturut -turut dari ketentuan S adalah:

S_Dif = 2, 4, 6, 8, ...

Karena perbedaan antara istilah berturut -turut tidak konstan, maka s itu bukan suksesi reguler. Ia harus tahu apakah itu kuadratik, untuk itu kita kembali membuat urutan perbedaan, memperoleh:

2, 2, 2, .. .

Karena semua ketentuan urutan diulang, dikonfirmasi bahwa S adalah suksesi kuadratik.

iii) suksesi s_Dif adalah biasa dan alasannya r adalah 2. Menggunakan persamaan yang ditunjukkan sebelumnya r = 2 ∙ A, tetap:

2 = 2 ∙ A, yang menyiratkan bahwa a = 1.

Istilah kedua dari suksesi perbedaan s_Dif Itu adalah 4 dan n-emem dari s_Dif adalah

A ∙ (2n+1)+b.

Istilah kedua memiliki n = 2. Juga ditentukan bahwa a = 1, jadi menggunakan persamaan sebelumnya dan menggantinya adalah:

4 = 1 ∙ (2 ∙ 2+1)+b

Kliring B diperoleh: b = -1.

Diketahui bahwa istilah kedua S bernilai 2, dan bahwa formula istilah umum harus dipenuhi dengan n = 2:

T_N = A ∙ n² + B ∙ N +C; n = 2; A = 1; B = -1; T₂ = 2

Artinya

2 = 1 ∙ 2² - 1 ∙ 2 + C

Disimpulkan bahwa C = 0, yaitu bahwa rumus yang memberikan istilah umum dari suksesi adalah:

T_N = 1 ∙ n² - 1 ∙ n +0 = n² - N

Sekarang istilah kelima diverifikasi:

T₅ = 5² - 5 = 20

iii) Gambar #10, yang belum ditarik di sini, akan memiliki area yang sesuai dengan istilah kesepuluh dari suksesi S:

T₁₀ = 10² - 10 = 90

Referensi

1. https: // www.Geogebra.org