Jumlah Sejarah Riemann, Rumus dan Properti, Latihan

Itu Jumlah Riemann Ini adalah nama yang menerima perkiraan perhitungan integral yang ditentukan, dengan jumlah jumlah yang bijaksana dengan nomor persyaratan yang terbatas. Aplikasi umum adalah pendekatan area fungsi dalam grafik.

Matematikawan Jerman Georg Friedrich Bernhard Riemann (1826-1866) yang menawarkan untuk pertama kalinya definisi yang ketat dari integral suatu fungsi dalam interval tertentu. Dia mengumumkannya dalam sebuah artikel yang diterbitkan pada tahun 1854. 

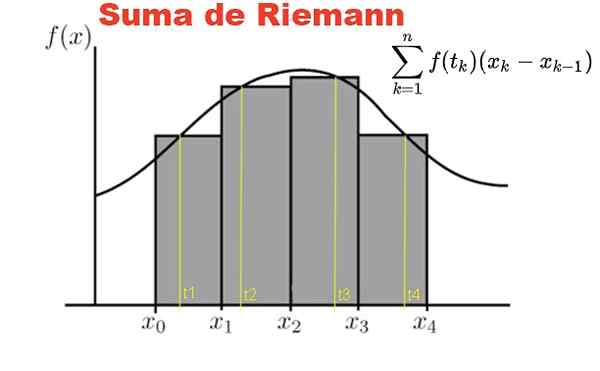
Gambar 1. Jumlah Riemann didefinisikan pada fungsi F dan partisi dalam interval [x0, x1]. Sumber: Fanny Zapata.

Jumlah Riemann didefinisikan pada fungsi y = f (x), dengan x milik interval tertutup [a, b]. Pada interval ini partisi P dari elemen N dibuat:

P = x₀= a, x₁, X₂,…, X_N= b

Ini berarti bahwa interval dibagi sebagai berikut:

 Di sini t_k adalah antara x_K-1 dan x_k:

X_K-1 ≤ t_k ≤ x_k

Gambar 1 menunjukkan jumlah Riemann dari fungsi F dalam interval [x₀, X₄] Pada partisi empat subinterval, persegi panjang abu -abu.

Jumlahnya mewakili luas total persegi panjang dan hasil dari jumlah ini adalah pendekatan numerik ke area di bawah kurva f, di antara absis x = x₀ y x = x₄.

Tentu saja, pendekatan ke area di bawah kurva sangat meningkat sejauh angka itu N partisi lebih besar.  Dengan cara ini jumlah konvergen ke area di bawah kurva, saat angka N Partisi cenderung tak terbatas.

[TOC]

Rumus dan properti

Jumlah fungsi F (x) Riemann pada partisi:

Dapat melayani Anda: rhomboid: karakteristik, cara mengeluarkan perimeter dan area

P = x₀= a, x₁, X₂,…, X_N= b

Didefinisikan pada interval [a, b], itu diberikan oleh:

S (p, f) = ∑_{K = 1}^N f (t_k) (X_k - X_K-1) 

Dimana t_k Itu adalah nilai dalam interval [x_k, X_K-1]. Dalam jumlah Riemann, interval reguler lebar biasanya digunakan Δx = (b - a)/n, di mana a dan b adalah nilai minimum dan maksimum absis, sedangkan n adalah jumlah subdivisi.

Dalam hal ini Jumlah Benar Riemann adalah:

Sd (f, n) = [f (a+Δx)+f (a+2Δx)+...+f (a+(n-1) Δx)+f (b)]*Δx

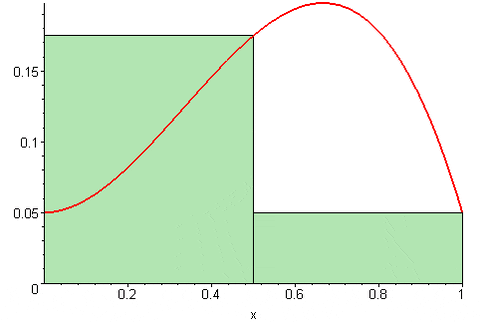Gambar 2. Jumlah Benar Riemann. Sumber: Wikimedia Commons. 09glasgow09 [cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0)].

Selagi Jumlah Kiri Riemann Itu dinyatakan sebagai:

Ya (f, n) = [f (a)+f (a+Δx)+...+f (a+(n-1) Δx)]*Δx

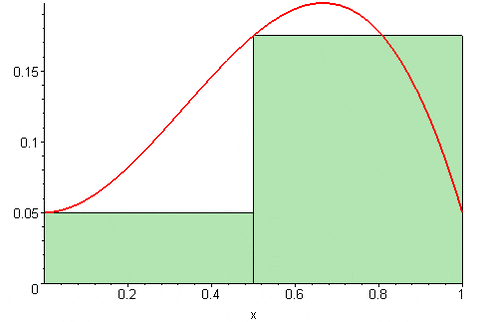Gambar 3. Jumlah Riemann tersisa. Sumber: Wikimedia Commons. 09glasgow09 [cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Akhirnya Jumlah Pusat Riemann adalah:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+...+f (b- Δx/2)]*Δx

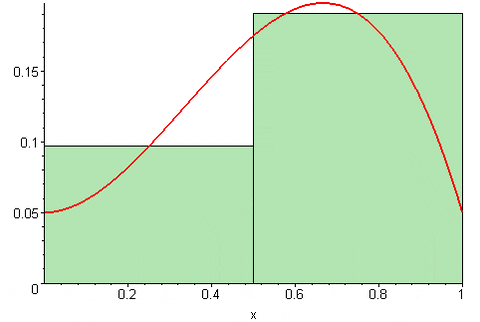Gambar 4. Jumlah menengah Riemann. Sumber: Wikimedia Commons. 09glasgow09 [cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Tergantung di mana titik T berada_k Dalam interval [x_k, X_K-1] Jumlah Riemann dapat melebih -lebihkan atau meremehkan nilai yang tepat dari area di bawah kurva fungsi y = f (x) (x). Yaitu, persegi panjang dapat unggul dari kurva atau sedikit di bawah ini.

Area di bawah kurva

Properti utama dari jumlah Riemann dan yang menjadi pentingnya, adalah bahwa jika jumlah subdivisi cenderung tak terbatas, hasil dari jumlah konvergen ke integral yang ditentukan dari fungsi:

Ekspresi sebelumnya sesuai dengan definisi integral Riemann dan berlaku asalkan fungsi F kontinu dan lunak. Untuk fungsi yang lebih khusus ada definisi lain dari integral (integral de stieldjes dan integral de lebesgue).

Itu dapat melayani Anda: kesalahan estimasi standar: bagaimana itu dihitung, contoh, latihan

Latihan terpecahkan

- Latihan 1

Hitung nilai integral yang didefinisikan antara a = -2 ke b = +2 dari fungsi:

f (x) = x²

Manfaatkan sejumlah Riemann. Untuk melakukan ini, temukan jumlah untuk partisi rutin interval [a, b] dan kemudian ambil batas matematika untuk kasus bahwa jumlah partisi menyimpan hingga tak terbatas. 

Larutan

Ini adalah langkah -langkah yang harus diikuti:

-Pertama, interval partisi didefinisikan sebagai: 

Δx = (b - a)/n. 

-Maka jumlah Riemann di sebelah kanan yang sesuai dengan fungsi f (x) seperti ini:

-Sekarang mereka diganti a = -2 dan b =+2, sehingga interval atau langkah Δx = 4/n. Artinya jumlah Riemann untuk fungsi f (x) = x² adalah:

-Kemudian binomial persegi dikembangkan: 

[-2 +(4i/n)]² = 4 - (16 i /n) + (4 /n)² yo²

-Dan kemudian diganti dengan cermat dalam jumlah:

-Langkah selanjutnya adalah memisahkan ringkasan dan menghapus jumlah konstan sebagai faktor umum dari setiap jumlah. Perlu untuk memperhitungkan bahwa indeksnya adalah saya, oleh karena itu angka dan ketentuan dengan N Mereka dianggap konstan:

-Setiap jumlah dievaluasi, karena untuk masing -masing ada ekspresi yang tepat. Misalnya, yang pertama dari ringkasan da n:

Yang kedua adalah:

 Dan yang ketiga adalah:

 -Mengganti hasil ringkasan dalam jumlah Riemann, akhirnya diperoleh:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Akhirnya Anda harus menghitung integral adalah:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5.333

Pembaca dapat memverifikasi bahwa ini adalah hasil yang tepat, yang dapat diperoleh dengan menyelesaikan integral yang tidak terbatas dan mengevaluasi batas integrasi oleh aturan Barrow.

Dapat melayani Anda: cara mengonversi dari km/h a m/s? Latihan terpecahkan

- Latihan 2

Tentukan kira -kira area di bawah fungsi: 

f (x) = (1/√ (2π) e^(-X2/2)

Antara x = -1 dan x =+1, menggunakan jumlah pusat Riemann dengan 10 partisi. Bandingkan dengan hasil yang tepat dan perkirakan perbedaan persentase.

Larutan

Langkah atau peningkatan antara dua nilai diskrit berturut -turut adalah:

Δx = (1 - (-1)/10 = 0.2

Sehingga partisi P di mana persegi panjang didefinisikan seperti ini:

P = -1,0; -0.8; -0,6; -0.4; -0,2; 0,0; 0.2; 0.4; 0.6; 0.8; 1.0

Tetapi seperti yang Anda inginkan adalah jumlah pusat, fungsi f (x) akan dievaluasi di titik tengah subinterval, yaitu di set:

T = -0.9; -0.7; -0.5; -0,3; -0,1; 0.1; 0.3; 0,5; 0.7; 0.9.

Jumlah Riemann (Tengah) seperti ini:

S = f (-0.9)*0.2 +f (-0.7)*0.2 +f (-0.5)*0.2 +… +f (0.7)*0.2 +f (0.9)*0.2

Karena fungsi F bersifat simetris, dimungkinkan untuk mengurangi jumlah menjadi hanya 5 istilah dan hasilnya dikalikan dengan dua:

S = 2*0,2*f (0,1)+ f (0,3)+ f (0,5)+ f (0,7)+ f (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

Fungsi yang diberikan dalam contoh ini tidak lain adalah bel Gauss yang diketahui (dinormalisasi, dengan rata -rata sama dengan nol dan standar deviasi). Diketahui bahwa area di bawah kurva dalam interval [-1,1] untuk fungsi ini adalah 0,6827.

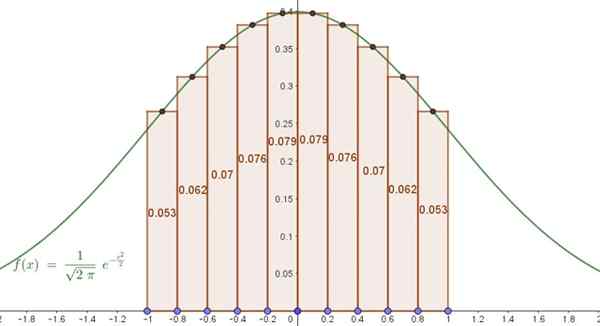Gambar 5. Area di bawah perkiraan Gauss Bell dengan jumlah sejumlah Riemann. Sumber: f. Zapata.

Ini berarti bahwa perkiraan solusi dengan hanya 10 istilah bertepatan dengan solusi yang tepat hingga tiga desimal. Persentase kesalahan antara perkiraan integral dan tepatnya adalah 0,07%.

Referensi

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Perhitungan komprehensif (ed diilustrasikan.). Madrid: editorial ESIC.
2. Unican. Sejarah konsep integral. Pulih dari: repositori.Unican.adalah
3. Uis. Jumlah Riemann. Pulih dari: matematika.Uis.Edu.bersama
4. Wikipedia. Jumlah Riemann. Pulih dari: is.Wikipedia.com
5. Wikipedia. Integrasi Riemann. Pulih dari: is.Wikipedia.com