Teorema Bernoulli

Kami menjelaskan apa teorema, persamaan, aplikasi dan menyelesaikan latihan Bernoulli

Apa Teorema Bernoulli?

Dia Teorema Bernoulli Dia menegaskan bahwa, dalam cairan ideal yang beredar di saluran, energi mekanik per unit volume fluida konstan di semua bagian tabung, terlepas dari bahwa mereka memiliki bagian transversal yang berbeda dari area dan tinggi.

Sekarang, cairan yang ideal adalah salah satu yang tidak dapat dikompresi, sehingga kepadatannya tetap, terlepas dari nilai tekanannya.

Selain itu, cairan yang ideal memiliki nol viskositas, yaitu, tidak ada gesekan antara lapisan fluida dan tidak ada antara cairan dan dinding saluran.

Kondisi ketidakmampuan dan viskositas nol sangat penting untuk menerapkan teorema Bernoulli. Juga perlu agar aliran diam, yaitu, alirannya tidak bervariasi dari waktu ke waktu.

Di sisi lain, alirannya harus laminar, sehingga tidak ada pusaran atau turbulensi selama perjalanan saluran.

Persamaan Bernoulli

Persamaan Bernoulli memiliki tiga istilah, pekerjaan yang dilakukan oleh pers, energi kinetik dan energi potensial gravitasi untuk setiap unit cairan kepadatan volumetrik ρ

Persamaan Bernoulli adalah:

Di sisi lain, persamaan kontinuitas menetapkan bahwa dalam cairan ideal, alirannya konstan di semua bagian tabung aliran. Yaitu, volume cairan dalam satuan waktu yang sama adalah sama di semua bagian tabung.

Jika alirannya q, maka:

Q = konstan

Dengan:

Q = a · v

Di mana A adalah area penampang tabung dan V adalah kecepatan cairan.

Dapat melayani Anda: satelit buatan

Perlu dicatat bahwa pada bagian tersempit tabung, cairan harus bersirkulasi lebih cepat, karena tetap konstan meskipun bervariasi. Oleh karena itu, energi kinetik per satuan volume lebih besar.

Karena teorema Bernoulli menetapkan bahwa energi mekanik konstan di semua bagian, di bagian yang lebih sempit dari energi kinetik yang lebih besar, energi potensial berkurang. 

Energi potensial terdiri dari energi gravitasi per unit volume ditambah pekerjaan yang dilakukan oleh tekanan dalam volume satuan, oleh karena itu, dengan mengurangi energi potensial juga mengurangi tekanan.

Singkatnya, efek gabungan dari prinsip kontinuitas dan teorema Bernoulli menghasilkan bagian sempit tabung aliran, di mana kecepatan fluida lebih besar, tekanan turun sehubungan dengan bagian yang lebih luas.

Istilah dalam persamaan Bernoulli

1) Pekerjaan yang dilakukan dengan tekanan per unit volume 

Di bagian penampang area ke, Cairan bergerak jumlah S, Karena tekanan P yang menghasilkan gaya f = p⋅ a.

Pekerjaan yang dilakukan dengan paksa adalah:

F⋅ s = p⋅ a⋅ s

Karena produk A⋅s mewakili volume yang dipindahkan, maka pekerjaan yang dilakukan per satuan volume cocok secara numerik dengan nilai P di bagian yang dipertimbangkan.

2) Energi kinetik dari satuan volume cairan

Karena cairan tidak dapat dimampatkan, kepadatannya memiliki nilai tetap yang disebut ρ.

Ketika fluida beredar melalui bagian penampang A, memindahkan jumlah S dalam waktu t, laju alirannya adalah:

Ini dapat melayani Anda: Hukum Kedua Termodinamika: Rumus, Persamaan, Contoh

V = S/T

Dan energi kinetik dari bagian cairan tersebut dihitung oleh:

K = ½ ρ (a⋅s) v²

Tetapi jika volume yang dipindahkan (A⋅s) adalah unit, maka istilah energi kinetik akan diberikan oleh ½ ρ v².

3) Energi potensial gravitasi volume unit cairan pada ketinggian h 

Untuk bagian cairan adonan M dan tinggi H Mengenai tingkat referensi tertentu, energi gravitasi diberikan oleh:

U = m⋅ g⋅ h

Jika adonan M Itu sesuai dengan bagian cairan kesatuan, kemudian massa bagian cocok dengan kepadatan ρ, Jadi energi potensial akan ρ⋅ g⋅ h.

Aplikasi Teorema Bernoulli

Dukungan aerodinamis

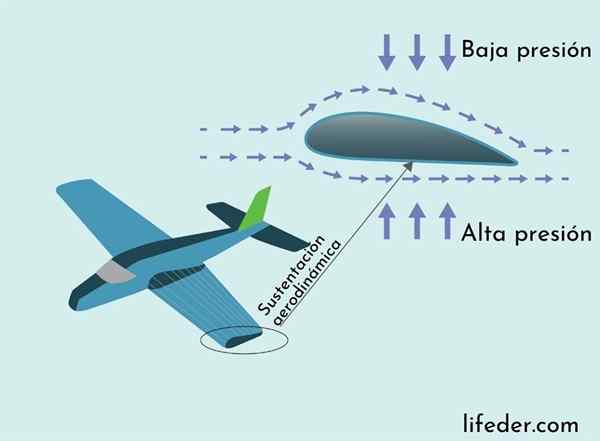Dukungan aerodinamik dijelaskan oleh teorema Bernoulli

Kekuatan yang mencegah pesawat dari penerbangan ke runtuh adalah kekuatan pendukung aerodinamik. Gaya pendukung bersih diarahkan secara vertikal ke atas dan bekerja di sepanjang sayap pesawat. Asal usulnya dijelaskan melalui teorema Bernoulli.

Sayap pesawat memiliki penampang dengan kurva yang lebih panjang di bagian atas dan lebih pendek di bagian bawah. Ini membuat rute udara di dekat permukaan sayap di bagian atas, sehingga udara mengalir lebih cepat di atas sayap daripada bagian bawah. 

Sebagai konsekuensi dari teorema Bernoulli, tekanan udara di bagian atas sayap yang bersirkulasi kurang dari pada bagian bawah, yang mengakibatkan gaya yang diberikan oleh perbedaan tekanan diarahkan ke atas, mendukung berat pesawat, menurutnya bisa terjadi terlihat di gambar berikut.

Ini dapat melayani Anda: Fisika selama orang -orang Yunani (Antige Yunani)

Peluncuran bola dan bola dengan efek kurva

Dalam beberapa olahraga seperti sepak bola, baseball dan cricke, pemain berpengalaman tahu caranya. Adalah apa yang disebut Peluncuran efek.

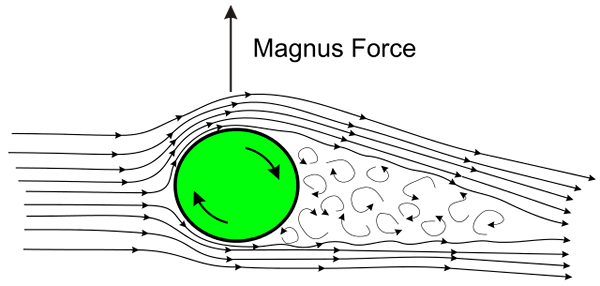Ilustrasi efek Magnus. Sumber: Wikimedia Commons

Efeknya terjadi setiap kali bola atau bola berputar dengan cepat saat bergerak di udara. Rotasi menyebabkan udara ke permukaan bola diseret olehnya dalam dua arah yang berlawanan, satu mendukung arah terjemahan dan, di sisi lain, terhadap arah perpindahan.

Sebagai akibat dari hambatan udara, area tekanan rendah diproduksi di permukaan bola dan pada wajah yang berlawanan dengan tekanan tinggi, menghasilkan gaya bersih yang mengalihkan lintasan alami bola bola.

Penjelasan fenomena ini dikenal sebagai Efek Magnus Itu berada tepat dalam teorema Bernoulli: di mana cairan bersirkulasi dengan cepat tekanannya rendah, dan di sisi di mana tekanan bersirkulasi lambat.

Olahraga diselesaikan

Tabung horizontal memiliki bagian area a₁ = 40 sentimeter persegi dan bagian lain dari bagian area a₂ empat kali lebih rendah. Jika aliran air adalah 6 l/s, tentukan perbedaan tekanan dan perbedaan tinggi dalam tabung vertikal.

Larutan 

Mulai dari persamaan aliran, yang nilainya q = 6 l/s:

Q = a · v

Anda harus kemudian kecepatan di bagian lebar adalah 1,5 m/s dan dalam peregangan sempit 6 m/s.

Kemudian, menerapkan dan mencocokkan persamaan Bernoulli pada peregangan lebar dan sempit, perbedaan tekanan 1700 PA diperoleh, yang sesuai dengan perbedaan tinggi dalam tabung vertikal 1,72 meter.