Teorema Euclid

Apa teorema Euclid?

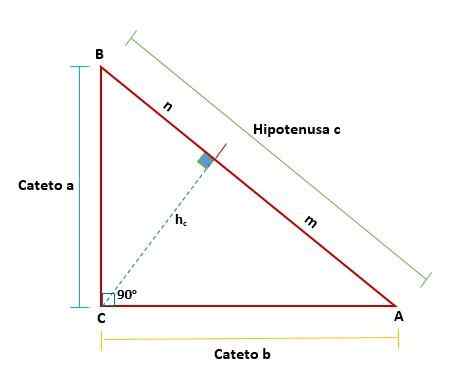
Dia Teorema Euclid Ini menunjukkan sifat -sifat segitiga kanan dengan menggambar garis yang membaginya menjadi dua persegi panjang baru yang mirip satu sama lain dan, pada gilirannya, mirip dengan segitiga asli; Jadi, ada hubungan proporsionalitas.

Euclides adalah salah satu ahli matematika dan geometer terbesar dari usia tua yang membuat beberapa demonstrasi teorema penting. Salah satu yang utama adalah nama yang menyandang namanya, yang memiliki aplikasi yang luas.

Ini telah demikian karena, melalui teorema itu, hubungan geometris yang ada di segitiga persegi panjang menjelaskan, di mana ini terkait dengan proyeksi mereka dalam hipotenuse.

Rumus dan demonstrasi

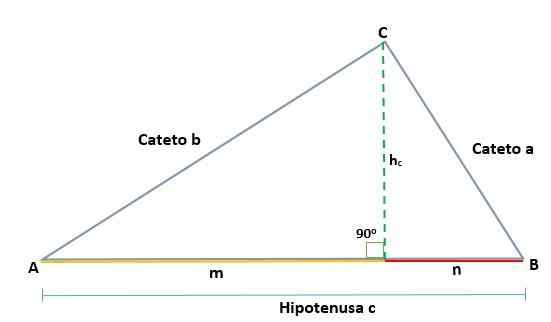
Teorema Euclid mengusulkan bahwa di setiap segitiga kanan, ketika garis ditarik - yang mewakili ketinggian yang sesuai dengan simpul sudut kanan sehubungan dengan hipotenus - dua persegi panjang terbentuk dari segitiga asli dari aslinya.

Segitiga ini akan mirip satu sama lain dan juga akan mirip dengan segitiga asli, yang berarti bahwa sisi yang sama sebanding satu sama lain:

Sudut -sudut dari tiga segitiga itu kongruen; Yaitu, ketika diputar pada 180 derajat di titiknya, sudut bertepatan di sisi lain. Ini menyiratkan bahwa setiap orang akan setara.

Dengan cara ini Anda juga dapat memverifikasi kesamaan yang ada di antara tiga segitiga, untuk kesetaraan sudutnya. Karena kesamaan segitiga, Euclid menetapkan proporsi ini dari dua teorema:

• Teorema Tinggi.
• Teorema Catetos.

Teorema ini memiliki aplikasi yang luas. Pada zaman kuno itu digunakan untuk menghitung ketinggian atau jarak, mewakili kemajuan besar untuk trigonometri.

Dapat melayani Anda: perhitungan pendekatan menggunakan diferensial

Saat ini diterapkan di berbagai bidang yang didasarkan pada matematika, seperti teknik, fisika, kimia dan astronomi, di antara banyak bidang lainnya.

Teorema Tinggi

Teorema ini menetapkan bahwa dalam segitiga persegi panjang apa pun, tinggi yang diambil dari sudut kanan sehubungan dengan hipotenusus adalah rata -rata proporsional geometris (kuadrat tinggi) antara proyeksi cotetos yang menentukan pada hipotenusus menggunakan hipotenus.

Artinya, kuadrat ketinggian akan sama dengan penggandaan kaki yang diproyeksikan yang membentuk hipotenus:

H_C² = m _* N

Demonstrasi

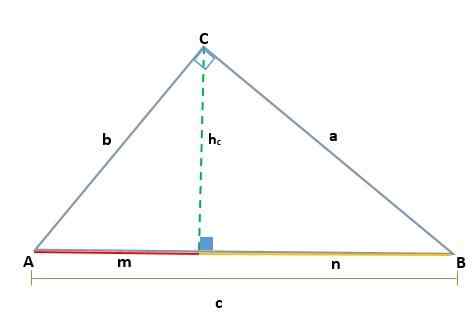
Diberi segitiga ABC, yang merupakan persegi panjang di Vertex C, dua persegi panjang serupa, ADC dan BCD dihasilkan; Oleh karena itu, sisi yang sesuai proporsional:

Sedemikian rupa_C Ini sesuai dengan segmen CD, sesuai dengan AB hypotenuse AB = C, jadi Anda harus:

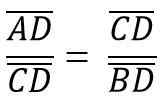
Pada gilirannya, ini sesuai dengan:

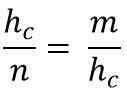
Membersihkan hipotenuse (h_C), Untuk melipatgandakan dua anggota kesetaraan, Anda harus:

H_{C *} H_{C =} M _* N

H_C² = m _* N

Dengan demikian, nilai hipotenus diberikan oleh:

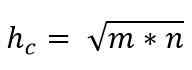
Teorema Catetos

Teorema ini menetapkan bahwa, dalam setiap segitiga kanan, ukuran masing -masing cateto akan menjadi rata -rata proporsional geometris (kuadrat dari setiap cateto) antara ukuran hipotenus (lengkap) dan proyeksi masing -masing di dalamnya:

B² = c _* M

ke² = c_* N

Demonstrasi

Diberikan segitiga ABC, yang merupakan persegi panjang di Vertex C, sehingga hipotenusnya adalah C, ketika menggambar ketinggian (h) proyeksi kategori A dan B ditentukan, yang merupakan segmen M dan N masing -masing, dan yang aktif The Hypotenuse.

Dengan demikian, tinggi yang ditarik pada segitiga persegi panjang ABC menghasilkan dua persegi panjang yang sama, ADC dan BCD, sehingga sisi yang sesuai proporsional, seperti ini:

Dapat melayani Anda: paraboloid hiperbolik: definisi, sifat, dan contoh

Db = n, yang merupakan proyeksi cateto CB pada hipotenuse.

AD = M, yang merupakan proyeksi cateto AC pada hipotenuse.

Kemudian, c hypotenuse ditentukan oleh jumlah kaki proyeksi:

C = m + n

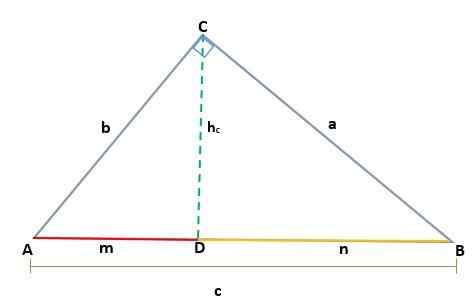
Karena kesamaan segitiga ADC dan BCD, Anda harus:

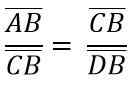
Di atas sama dengan:

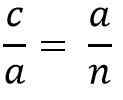
Membersihkan cateto "A" untuk melipatgandakan dua anggota kesetaraan, Anda harus:

ke _* a = c _* N

ke² = c _* N

Dengan demikian, nilai cateto "a" diberikan oleh:

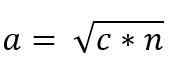
Demikian pula, karena kesamaan segitiga ACB dan ADC, Anda harus:

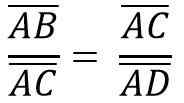
Di atas sama dengan:

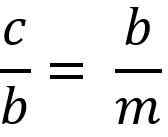
Membersihkan cateto "B" untuk melipatgandakan dua anggota kesetaraan, Anda harus:

B _* b = c _* M

B² = c _* M

Dengan demikian, nilai cateto "b" diberikan oleh:

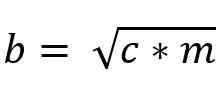
Hubungan antara teorema euclid

Teorema dengan mengacu pada ketinggian dan kategori saling terkait karena ukuran keduanya dibuat sehubungan dengan hipotenuse dari segitiga persegi panjang.

Melalui hubungan teorema Euclid, nilai tinggi juga dapat ditemukan; Itu dimungkinkan dengan membersihkan nilai m dan n dari teorema kategori dan diganti dalam teorema tinggi. Dengan cara ini, terpenuhi bahwa tinggi sama dengan penggandaan kaki, dibagi dengan hipotenus:

B² = c _* M

m = b² ÷ c

ke² = c _* N

n = a² ÷ c

Di Teorema Tinggi M dan N diganti:

H_C² = m _* N

H_C² = (b² ÷ c) _* (ke² ÷ c)

H_C = (b² _* ke²) ÷ c

Latihan terpecahkan

Contoh 1

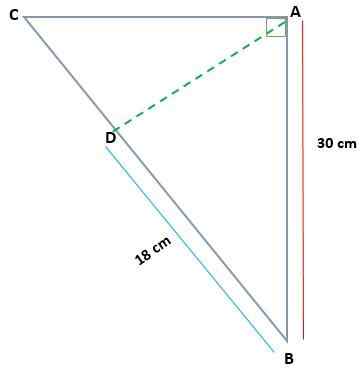
Mengingat segitiga ABC, persegi panjang dalam A, tentukan ukuran AC dan AD, jika AB = 30 cm dan BD = 18 cm

Larutan

Dalam hal ini ada langkah -langkah dari salah satu kaki yang diproyeksikan (BD) dan salah satu TARK dari segitiga asli (AB). Dengan begitu Anda dapat menerapkan teorema kategori untuk menemukan nilai cateto BC.

Dapat melayani Anda: aturan korespondensi suatu fungsi

AB² = Bd _* Bc

(30)² = 18 _* Bc

900 = 18 _* Bc

BC = 900 ÷ 18

Bc = 50 cm

Nilai cateto CD dapat ditemukan mengetahui bahwa BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Sekarang dimungkinkan untuk menentukan nilai cateto AC, menerapkan lagi teorema kategori:

Ac² = CD _* Bd

Ac² = 32 _* lima puluh

Ac² = 160

Ac = √1600 = 40 cm

Untuk menentukan nilai ketinggian (AD), teorema tinggi berlaku, karena nilai -nilai kategori yang diproyeksikan CD dan BD diketahui:

IKLAN² = 32 _* 18

IKLAN² = 576

AD = √576

Iklan = 24 cm

Contoh 2

Tentukan nilai tinggi (h) segitiga MNL, persegi panjang di N, mengetahui langkah -langkah segmen:

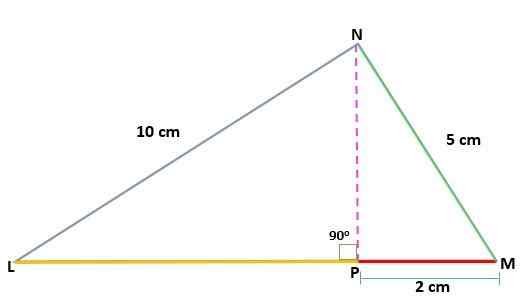
Nl = 10 cm

Mn = 5 cm

PM = 2 cm

Larutan

Anda memiliki ukuran salah satu kaki yang diproyeksikan pada hypotenuse (PM), serta ukuran kategori segitiga asli. Dengan begitu Anda dapat menerapkan teorema kategori untuk menemukan nilai cateto yang diproyeksikan lainnya (ln):

Nl² = PM _* LM

(10)² = 5 _* LM

100 = 5 _* LM

PL = 100 ÷ 5 = 20

Karena nilai kategori dan hipotenus sudah diketahui, melalui hubungan teorema tinggi dan kategori dapat ditentukan nilai ketinggian:

Nl = 10

Mn = 5

LM = 20

H = (b² _* ke²) ÷ c.

H = (10² _* 5²)  ÷ (dua puluh)

H = (100 _* 25) ÷ (dua puluh)

H = 2500 ÷ dua puluh

H = 125 cm.