Teorema Hijau, Demonstrasi, Aplikasi dan Latihan

Dia Teorema Hijau Ini adalah metode perhitungan yang digunakan untuk menghubungkan integral garis dengan area ganda atau integral permukaan. Fungsi yang terlibat harus dilambangkan sebagai vektor dan bidang yang ditentukan dalam lintasan C.

Misalnya, ekspresi garis integral bisa sangat rumit untuk dipecahkan; Namun, dalam menerapkan teorema Green, integral ganda menjadi cukup mendasar. Selalu penting untuk menghormati arti positif dari lintasan, ini mengacu pada arah jarum jam.

Teorema Green adalah kasus khusus teorema Stokes, di mana proyeksi fungsi vektor dilakukan di bidang XY.

[TOC]

Definisi

Ekspresi Teorema Green Green adalah sebagai berikut:

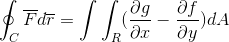
Dalam istilah pertama, garis integral yang ditentukan oleh lintasan "c" diamati, dari skalar produk antara fungsi vektor "f" dan vektor "r".

C: Ini adalah lintasan yang ditentukan di mana fungsi vektor akan diproyeksikan selama didefinisikan untuk bidang itu.

F: Fungsi vektor, di mana masing -masing komponennya didefinisikan oleh fungsi seperti itu (f, g).

A: Ini adalah garis singgung vektor ke wilayah R di mana integral didefinisikan. Dalam hal ini dioperasikan dengan perbedaan vektor ini.

Dalam istilah kedua kita melihat teorema yang dikembangkan hijau, di mana integral ganda yang didefinisikan di wilayah r dari perbedaan turunan parsial G dan F diamati, sehubungan dengan x dan dan masing -masing. Untuk diferensial area yang tidak lebih dari produk dari kedua diferensial dua dimensi (DX.dy).

Teorema ini sangat berlaku untuk integral ruang dan permukaan.

Demonstrasi

Untuk menunjukkan teorema Green dengan cara yang sederhana, tugas ini akan dipecah menjadi 2 bagian. Pertama kita akan berasumsi bahwa fungsi vektor f hanya memiliki definisi di sasaran yo. Sedangkan fungsi "g" yang sesuai dengan versor J akan sama dengan nol.

Dapat melayani Anda: berapa banyak ratusan yang pas di sepersepuluh? (Contoh)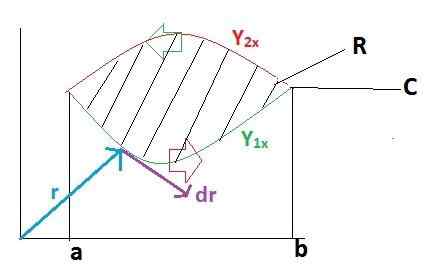Pengarang

F = f (x, y)yo + G (x, y)J = f (x, y)yo + 0

R = xyo + DanJ

DR = DXyo + DyJ

Pertama -tama kami mengembangkan garis integral di atas lintasan C, yang lintasannya telah disepsi dalam 2 bagian yang lebih dulu dari A ke B dan setelah B ke A.

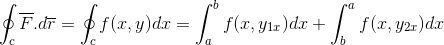
Definisi teorema mendasar dari perhitungan untuk integral yang ditentukan diterapkan.

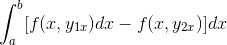
Ekspresi disusun kembali dalam satu integral, dibuat umum untuk negatif dan urutan faktor -faktor dibalik.

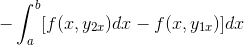
Dengan mengamati secara rinci ekspresi ini, menjadi jelas bahwa ketika menerapkan kriteria fungsi primitif, ia berada di hadapan integral dari ekspresi yang berasal dari F sehubungan dengan dan. Dievaluasi dalam parameter

[Dan_1x , Dan_2x]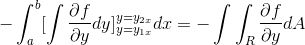

Sekarang sudah cukup untuk mengasumsikan bahwa fungsi menyenangkan vektor hanya didefinisikan untuk g (x, y)J. Di mana ketika beroperasi dengan cara yang dihomologis ke kasus sebelumnya, itu diperoleh:

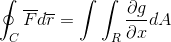
Akhirnya, 2 demonstrasi diambil dan bergabung dalam kasus di mana fungsi vektor mengambil nilai untuk kedua versor. Dengan cara ini ditampilkan sebagai garis integral setelah mendefinisikan dan dianggap sebagai lintasan satu -dimensi, itu dapat sepenuhnya dikembangkan untuk bidang dan ruang.

F = f (x, y)yo + G (x, y)J

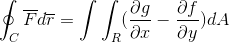
Dengan cara ini teorema Green ditunjukkan.

Aplikasi

Aplikasi teorema hijau luas di cabang fisika dan matematika. Ini meluas ke aplikasi atau penggunaan apa pun yang dapat diberikan untuk integrasi garis.

Pekerjaan mekanis yang dilakukan oleh gaya F melalui lintasan C, dapat dikembangkan dengan garis integral yang dinyatakan sebagai integral ganda dari suatu daerah melalui teorema Green.

Dapat melayani Anda: prisma pentagonal: karakteristik, bagian, simpul, tepi, volume

Saat -saat inersia dari banyak badan yang mengalami kekuatan eksternal pada titik aplikasi yang berbeda, juga menanggapi integral yang dapat dikembangkan dengan teorema Green.

Ini memiliki banyak fungsi dalam studi resistensi bahan yang sedang digunakan. Di mana nilai eksternal dapat dikuantifikasi dan dipertimbangkan sebelum elaborasi berbagai elemen.

Secara umum, teorema Green memfasilitasi pemahaman dan definisi area di mana fungsi vektor didefinisikan sehubungan dengan suatu wilayah menurut lintasan.

Sejarah

Itu diterbitkan pada tahun 1828 dalam karya itu Analisis Matematika untuk Teori Listrik dan Magnet, Ditulis oleh ahli matematika Inggris George Green. Ini mengeksplorasi bagian yang cukup menentukan dalam penerapan perhitungan dalam fisika, seperti konsep potensial, fungsi hijau dan aplikasi teorema mobilnya berjudul.

George Green memformalkan karier muridnya pada usia 40, sejauh ini seorang matematika yang benar -benar diizinkan sendiri. Setelah belajar di University of Cambridge, penelitiannya berlanjut, memberikan kontribusi di bidang akustik, optik dan hidrodinamika yang masih berlaku sampai sekarang.

Hubungan dengan teorema lain

Teorema Green adalah kasus khusus, dan muncul dari 2 teorema lain yang sangat penting di cabang perhitungan. Ini adalah teorema Kelvin-Stokes dan Divergence atau Teorema Gausski.

Mulai dari kedua teorema Anda dapat mencapai teorema Green. Definisi dan proposisi tertentu diperlukan untuk mengembangkan demonstrasi ini.

Latihan

- Latihan berikut menunjukkan bagaimana mengubah garis integral menjadi integral ganda sehubungan dengan wilayah R.

Ekspresi aslinya adalah sebagai berikut:

Dapat melayani Anda: berapa nilai x?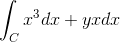

Dan harus dievaluasi di wilayah segitiga yang bergabung dengan titik (0, 0), (1, 0), (0, 1) dilambangkan dengan C. Untuk kasus ini, rasa positif dari giliran akan dipertimbangkan.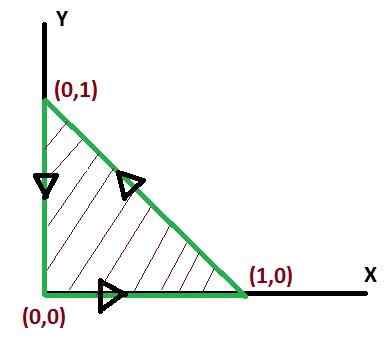

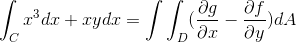
Dari mana fungsi yang sesuai dengan f dan g diambil dari

f (x, y) = x³                      g (x, y) = yx

df/dy = 0 dg/dx = y

Penting untuk mendefinisikan fungsi yang membentuk batas wilayah C, untuk dapat mengumpulkan produk diferensial yang akan sepenuhnya menutupi wilayah tersebut.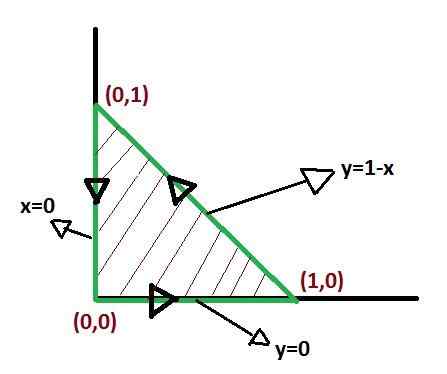

Tidak ada cara unik untuk mendefinisikan batas integrasi saat menerapkan teorema Green. Tetapi ada bentuk di mana integral setelah didefinisikan bisa lebih sederhana. Sedemikian rupa sehingga optimalisasi batas integrasi patut mendapat perhatian.

Untuk kasus ini ungkapan ini dipertimbangkan: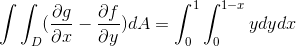

Dimana dalam menyelesaikan integral yang kita peroleh:

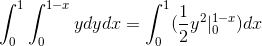
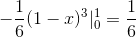
Nilai ini sesuai dengan unit kubik dengan wilayah di bawah fungsi vektor dan pada wilayah segitiga yang ditentukan oleh c.

Dalam hal garis integral tanpa melakukan metode hijau, akan diperlukan untuk parameterisasi fungsi di setiap bagian wilayah tersebut. Yaitu, buat 3 integral parameter untuk resolusi. Ini adalah bukti yang cukup dari keefektifan yang dikontribusikan oleh Robert Green dengan teorema tersebut terhadap perhitungan.

Referensi

1. Pengantar Mekanika Continum. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 Jul. 2009
2. Kalkulus multivariabel. James Stewart. Pembelajaran Cengage, 22 Mar. 2011
3. Sejarah informal teorema Green dan ide -ide terkait. James Joseph Cross. Departemen Matematika, Universitas Melbourne, 1975
4. Perilaku Panas Menggunakan Fungsi Hijau. Kevin d. Cole, James V. Beck, a. Haji-Sheikh, Bahman Luckouhi. Taylor & Francis, 16 Jul. 2010
5. Penerapan teorema Green untuk ekstremisasi integral linier. Pusat Informasi Teknis Pertahanan, 1961