Teorema Penjelasan, Aplikasi, Latihan Steiner

Dia Teorema Steiner, juga dikenal sebagai Teorema Sumbu Paralel, Ini memungkinkan untuk mengevaluasi momen inersia dari tubuh yang diperluas, di sekitar sumbu yang sejajar dengan yang lain yang melewati pusat massa objek.

Itu ditemukan oleh matematika Swiss_Cm Momen inersia objek sehubungan dengan sumbu yang melewati pusat massa CM dan I -nya_z Momen inersia sehubungan dengan sumbu paralel lain untuk ini.

Gambar 1. Pintu persegi panjang yang menyalakan kegembiraannya memiliki momen inersia yang dapat dihitung dengan menerapkan teorema Steiner. Sumber: Pixabay.

Diketahui jarak d yang memisahkan kedua sumbu dan massa m dari tubuh yang dimaksud, momen inersia sehubungan dengan sumbu penyamaran adalah:

yo_z = I_Cm + Md²

Momen inersia menunjukkan betapa mudahnya suatu objek untuk berputar di sekitar sumbu tertentu. Itu tidak hanya tergantung pada tubuh tubuh, tetapi pada bagaimana itu didistribusikan. Karena alasan ini juga dikenal sebagai Inersia rotasi, Menjadi unit Anda di sistem KG internasional . M².

Teorema menunjukkan bahwa momen inersia yo_z Itu selalu lebih besar dari momen inersia yo_Cm dalam jumlah yang diberikan oleh M.D².

[TOC]

Aplikasi

Karena suatu objek dapat berputar di sekitar banyak sumbu, dan di tabel biasanya hanya momen inersia mengenai sumbu yang melewati centroid, teorema Steiner memfasilitasi perhitungan ketika perlu memutar tubuh pada as roda yang tidak bertepatan dengan ini.

Dapat melayani Anda: Gerakan Bujur Barat: Karakteristik, Jenis dan Contoh

Misalnya, pintu umumnya tidak berputar di sekitar sumbu yang melewati pusat massanya, tetapi sehubungan dengan sumbu lateral, di mana engsel menempel.

Saat mengetahui momen inersia, dimungkinkan untuk menghitung energi kinetik yang terkait dengan rotasi pada sumbu ini. Ya K adalah energi kinetik, yo momen inersia di sekitar poros yang dimaksud dan Ω Kecepatan sudut terpenuhi bahwa:

K = ½ i.Ω²

Persamaan ini sangat mirip dengan formula energi kinetik yang sangat akrab untuk objek massa M bergerak dengan kecepatan v:  K = ½ m.v². Dan apakah saat inersia atau inersia rotasi yo bermain secara rotasi peran yang sama dengan adonan M Dalam terjemahan.

Demonstrasi teorema Steiner

Momen inersia dari objek yang diperluas didefinisikan sebagai:

I = ∫R² DM

Di mana DM Ini adalah massa massa yang sangat kecil dan R Itu adalah jarak antara DM dan sumbu rotasi z. Pada Gambar 2 sumbu ini melintasi pusat massa CM, namun itu bisa menjadi siapa pun.

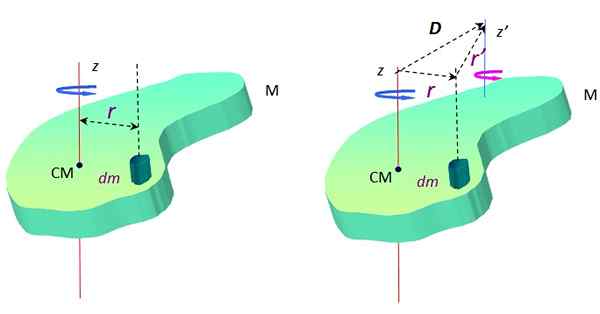Gambar 2. Sebuah objek yang diperpanjang dalam rotasi di sekitar dua sumbu paralel. Sumber: f. Zapata.

Di sekitar poros lain  z ', Momen inersia adalah:

yo_z= ∫ (R ')² DM

Sekarang, menurut segitiga yang dibentuk oleh vektor D, R Dan R ' (Lihat Gambar 2 di sebelah kanan), ada jumlah vektor:

R + R ' = D   → R ' = D - R

Tiga vektor berada di bidang objek yang bisa menjadi Xy. Asal usul sistem koordinat (0,0) dipilih dalam cm untuk memfasilitasi perhitungan yang mengikuti.

Dengan cara ini modul persegi vektor R ' adalah:

Dapat melayani Anda: Biofisika: Sejarah, Studi Apa, Aplikasi, Konsep, Metode

(R ')² = (D_X- R_X)² +(D_Dan - R_Dan)² =

= D_X² + D_Dan² +R_X² + R_Dan2 -2d_XR_X - 2 d_DanR_Dan =

= D² + R²  - 2d_XR_X - 2 d_DanR_Dan

Sekarang perkembangan ini digantikan dalam integral momen inersia i_z dan juga definisi kepadatan DM = ρ digunakan.DV:

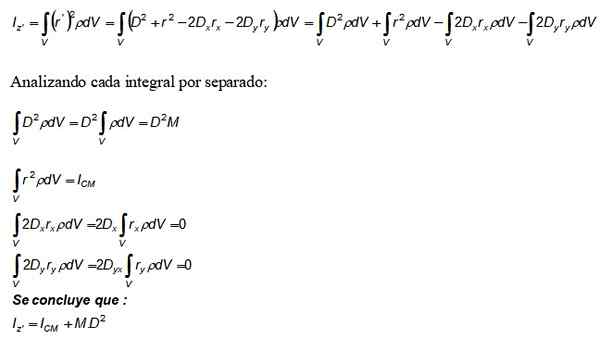
Istilah m. D² Yang muncul dalam teorema Steiner berasal dari integral pertama, yang kedua adalah momen inersia mengenai sumbu yang melewati CM.

Untuk bagiannya, integral ketiga dan keempat bernilai 0, karena menurut definisi mereka merupakan posisi CM, yang telah dipilih sebagai asal sistem koordinat (0,0).

Latihan terpecahkan

-Latihan diselesaikan 1

Pintu persegi panjang pada Gambar 1 memiliki massa 23 kg, lebar 1,30 dan 2,10 m tinggi. Tentukan momen inersia pintu mengenai sumbu yang melewati kegembiraan, dengan asumsi bahwa pintu itu tipis dan seragam.

Gambar 3. Skema untuk contoh diselesaikan 1. Sumber: Pixabay yang dimodifikasi.

Larutan

Dari tabel momen inersia, untuk pelat persegi panjang massa dan dimensi ke Dan B, Momen inersia sehubungan dengan sumbu yang melewati pusat massa adalah: i_Cm = (1/12)M(ke² + B²).

Pintu yang homogen akan diasumsikan (pendekatan, karena pintu sosok itu mungkin tidak begitu banyak). Dalam hal ini, pusat massa melewati pusat geometrisnya. Pada Gambar 3, sumbu yang melewati pusat massa telah ditarik dan yang juga sejajar dengan sumbu yang melewati kegembiraan.

yo_Cm = (1/12) x 23 kg x (1.30²+2.10²) M² = 11.7 kg.M²

Dapat melayani Anda: apa itu geoid?

Menerapkan teorema Steiner untuk sumbu rotasi hijau:

I = i_Cm + Md² = 11.7 kg.M² + 23 kg x 0.652 m² = 21.4 kg.

-Latihan diselesaikan 2

Temukan momen inersia dari batang homogen tipis ketika berputar sehubungan dengan sumbu yang melewati salah satu ujungnya, lihat gambar. Apakah lebih besar atau kurang dari momen inersia ketika berputar di sekitar pusatnya? Karena?

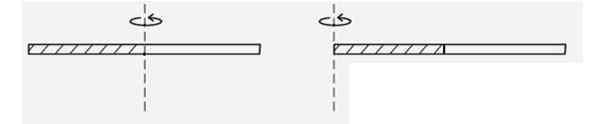Gambar 4. Skema untuk contoh terpecahkan 2. Sumber: f. Zapata.

Larutan

Menurut momen inersia, momen inersia yo_Cm dari batang adonan tipis M dan panjangnya L adalah: yo_Cm = (1/12) ml²

Dan teorema Steiner menyatakan bahwa ketika diputar di sekitar sumbu yang melewati satu ujung d = l/2 tetap:

I = i_Cm + Md² = (1/12) ml² + M (l/2)² = (1/3) ml²

Sudah tua.

Pengaruh jarak ke sumbu rotasi tidak linier, tetapi kuadratik. Massa yang dua kali lipat jarak yang lain akan memiliki momen inersia sebanding dengan (2d)² = 4d².

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 313-340.
2. Universitas Negeri Georgia. Gerakan Rotasi. Pulih dari: Phys.Nthu.Edu.Tw.
3. Teorema Sumbu Paralel. Pulih dari: hyperphysics.Phy-astr.GSU.Edu.
4. Rex, a. 2011. Dasar -dasar fisika. Pearson. 190-200.
5. Wikipedia. Teorema Sumbu Paralel. Diperoleh dari: di.Wikipedia.org