Miletus teorema seperti itu

Kami menjelaskan teorema pertama dan kedua dari itu, dengan contoh dan latihan diselesaikan

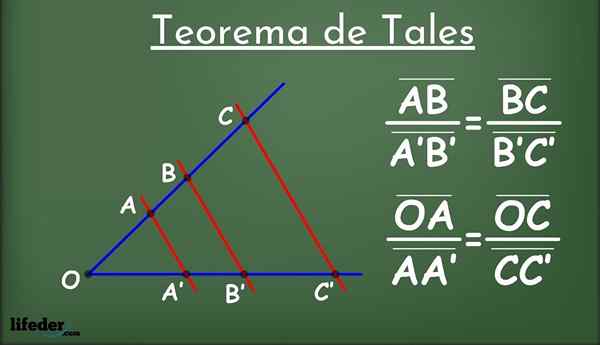
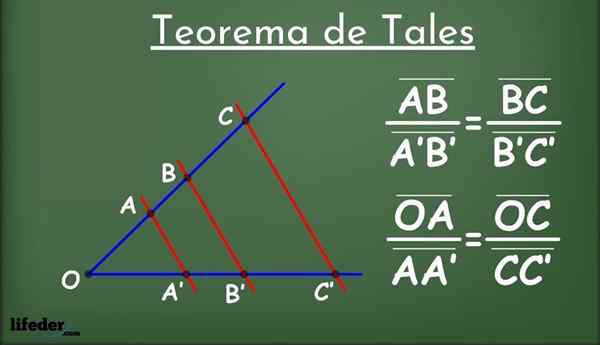Gambar 1.- Teorema Tales

Apa itu?

Dia Teorema seperti itu Dari Miletus ia benar -benar mengacu pada beberapa teorema geometri yang dikaitkan dengan bijak Yunani Kuno Thales of Miletus, yang hidup dari 624 hingga 546 AC di Miletus, Turki saat ini.

Selain ahli matematika dan geometer, seperti itu adalah seorang filsuf yang diakui karena ketajamannya yang luar biasa. Dikatakan bahwa ia berhasil mengukur ketinggian piramida besar melalui penggunaan salah satu teorema.

Dia Teorema pertama seperti itu Ini mengacu pada segmen yang ditentukan oleh sekelompok garis paralel dalam dua garis di pesawat. Segmen -segmen ini menyimpan rasio proporsionalitas, seperti yang akan dilihat segera, yang diperluas ke sisi dua segitiga, asalkan kondisi tertentu terpenuhi.

Teorema ini sangat berguna dalam praktiknya, karena memungkinkan untuk menentukan ketinggian sangat tinggi atau sulit untuk mengakses struktur, tanpa perlu mengukurnya secara langsung. Inilah tepatnya apa yang dilakukan Tales ketika dia mengukur ketinggian piramida besar.

Untuk bagiannya, Teorema kedua ini Titik tautan milik keliling dengan segitiga persegi panjang yang terdaftar di dalamnya, yang hypotenuse bertepatan dengan diameternya.

Teorema pertama seperti itu

Menjadi dua garis di pesawat, disebut l₁ dan saya₂ (Biru dalam Gambar 1) dan sekelompok garis sejajar satu sama lain (merah) yang berpotongan l₁ dan saya₂.

Garis paralel membagi garis menjadi segmen l₁ dan saya₂: Ab, a'b ', bc, b'c' dan sebagainya. Di antara segmen yang dihadapi, hubungan proporsionalitas berikut ditetapkan:

Sebagai contoh, dalam gambar ini, ukuran segmen "X" dihitung oleh teorema tersebut, karena garis -garis tersebut berpotongan dengan beberapa paralel yang menentukan segmen dengan panjang yang diketahui:

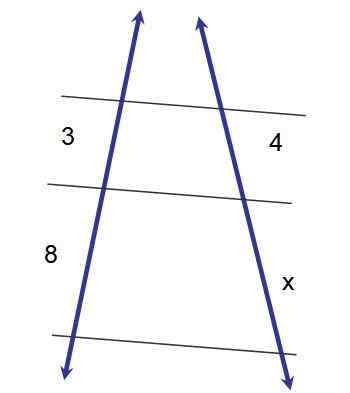Itu dapat melayani Anda: acara yang saling eksklusif: properti dan contohGambar 2.- Penerapan teorema pertama untuk menentukan ukuran segmen x. Sumber: f. Zapata.

3x = 32

x = 32/3 ≈ 10.7

Teorema semacam itu untuk segitiga yang sama

Teorema dapat diperluas ke segitiga sebagai berikut: Misalkan ada segitiga ABC di mana segmen paralel ditarik ke salah satu sisinya. Dengan cara ini dua segitiga serupa diperoleh: ABC dan DEC, yang sudut internalnya kongruen, yaitu, mereka memiliki ukuran yang sama.

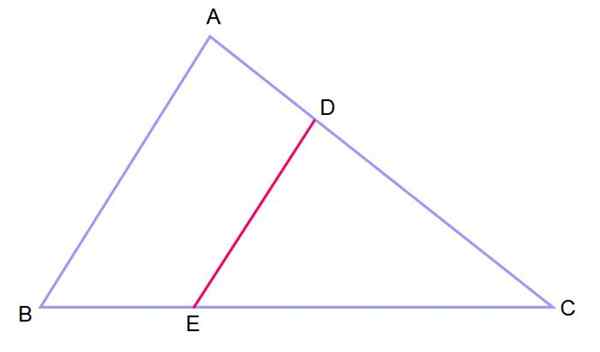Gambar 3.- Dua segitiga dalam posisi seperti itu, dengan dua sisi paralel dan sudut umum, serupa. Sumber: f. Zapata.

Ketika Anda memiliki dua segitiga yang diatur dengan cara ini, dikatakan bahwa mereka berada dalam posisi seperti itu.

Rasio proporsionalitas antara segmen dinaikkan dengan cara yang sama seperti untuk garis paralel:

Yang setara dengan yang lain ini, antara sisi yang sesuai dari masing -masing segitiga, juga disebut sisi homolog:

Masing -masing kutipan ini disebut alasan kesamaan. Dalam segitiga yang sama, alasan kesamaan sama dengan hasil bagi antara perimeter dan kuadrat dari rasio kesamaan sama dengan hasil bagi antara area.

Selanjutnya, contoh di mana teorema tersebut dapat diterapkan pada segitiga yang serupa dan mencari tahu berapa nilai Sisi X yang tidak diketahui.

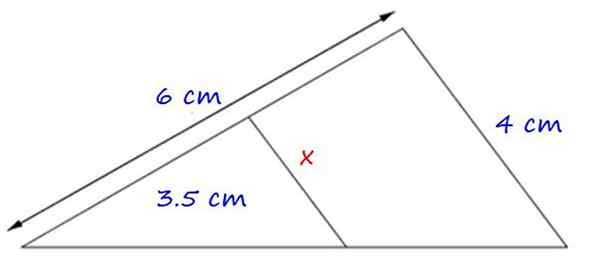Gambar 4.- Contoh aplikasi dari teorema pertama seperti itu. Sumber: f. Zapata.

Segitiga yang terbentuk serupa, karena memiliki sudut yang sama dan sisi x dan 4 cm paralel.

Oleh karena itu proporsionalitas antara sisi yang sesuai adalah:

Dan nilai x mudah dibersihkan:

x = (4 × 3.5) ÷ 6 cm = 2.3 cm

Teorema kedua ini

Teorema ini mengacu pada segitiga yang simpulnya adalah titik -titik yang dimiliki oleh lingkar, yang berarti terdaftar di dalamnya.

Dalam hal ini, teorema menetapkan bahwa setiap kali hipotenusa sesuai dengan diameter lingkar, segitiga yang dilacak adalah persegi panjang, yaitu, salah satu sudut internalnya berukuran 90º, seperti yang terlihat pada Gambar 5 ke kiri.

Dapat melayani Anda: simbolisasi ekspresi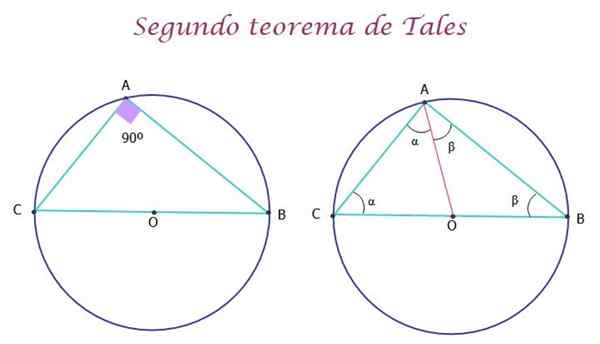Gambar 5.- Teorema kedua dari menyatakan bahwa segitiga yang terdaftar di lingkar adalah persegi panjang. Sumber: f. Zapata.

Demonstrasi teorema kedua dari seperti itu

Demonstrasi teorema sangat sederhana. Pada gambar di atas kanan, segmen AO telah ditarik berwarna merah, untuk membentuk dua segitiga AOC dan AOB, yang merupakan isosceles, karena sisi OA, OC dan OB adalah radio dari keliling dan oleh karena itu mereka mengukur hal yang sama.

Dengan cara ini, segitiga memiliki dua sudut yang sama, yang masing -masing α dan β. Sekarang, untuk segitiga ABC asli, seperti untuk segitiga apa pun, dipenuhi bahwa jumlah ukuran sudut internalnya sama dengan 180º, oleh karena itu: oleh karena itu::

α + (α + β) + β = 180º

Karena itu:

2α + 2β = 180º

Karena itu:

2 (α +β) = 180º

α +β = 90º

Yang membuktikan bahwa segitiga ABC memiliki sudut internal 90º dan karenanya merupakan segitiga siku -siku.

Contoh

Pada gambar berikut ini segitiga ABC adalah Isosceles dan Rectangle (isorectangle segitiga), menjadi perimeter keliling sama dengan 25 cm. Berapa segmen AC dan AB?

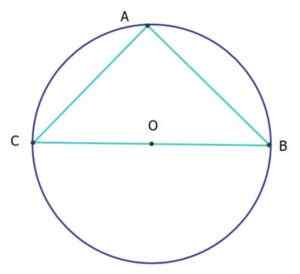
Perimeter keliling adalah panjangnya L, yang diberikan tergantung pada diameternya D dengan formula:

L = πd

Oleh karena itu diameter, yang merupakan segmen CB, mengukur:

D = cb = l/ π = 25 cm/ π = 7.96 cm.

Karena segitiga adalah Isosceles, ini berarti bahwa sudut akutnya masing -masing mengukur 45º. Karena hipotenus dari segitiga adalah diameter keliling, rasio trigonometri 45 dapat digunakan, misalnya:

Sen 45º = ac/cb

Ac = cb × sin 45º = 7.96 cm × sin 45º = 5.64 cm

Dapat melayani Anda: Teorema Moivre

Sisi AB memiliki ukuran yang sama: 5.64 cm, karena segitiga adalah Isosceles.

Aplikasi teorema tersebut

Teorema pertama tersebut dapat digunakan untuk mengetahui jarak yang tidak mudah diukur. Dikatakan bahwa perjalanan seperti itu ke Mesir dan di sana menentukan, dengan cara yang sangat cerdik, puncak piramida besar.

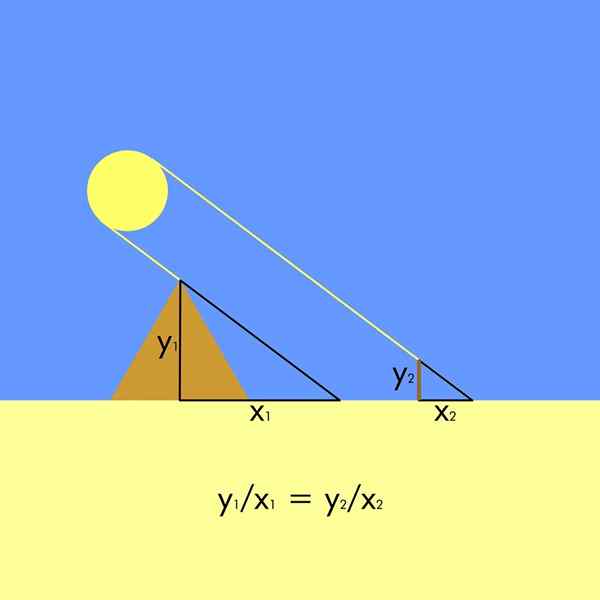
Untuk ini perlu. Dengan demikian, dua segitiga serupa terbentuk, karena sinar matahari memiliki insiden paralel.

Pada gambar, ketinggian piramida adalah dan₁ Dan bayangannya adalah x₁, Sedangkan ketinggian tiang pancang dan₂ (Beberapa penulis sejarah mengklaim bahwa seperti itu menggunakan tinggi badan mereka sendiri) dan bayangan mereka adalah x₂. Karena segitiga serupa, hubungan proporsionalitas berikut terbentuk:

Menjadi sangat mudah untuk membersihkan ketinggian piramida dan₁:

Dan₁ = x₁∙ (dan₂ ÷ x₂)

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Requena, b. Teorema seperti itu. Pulih dari: universoformulas.com.
3. Aula Matematika. Tales de Mileto dan The Great Pyramid. Diperoleh dari: Salonmatematic.com
4. Bahan superprof didaktik. Miletus seperti itu. Pulih dari: superprof.adalah.
5. Thales dan Teorema Rupa. Dua masalah yang sangat lama. Pulih dari: edu.Xunta.Gal.