Teorema Torricelli

Apa teorema Torricelli?

Dia Teorema Torricelli o Prinsip Torricelli menyatakan bahwa kecepatan cairan yang keluar melalui lubang di dinding tangki atau wadah, identik dengan mana suatu objek memperoleh yang dijatuhkan secara bebas dari ketinggian yang sama dengan permukaan cairan bebas ke Lubang.

Teorema diilustrasikan pada gambar berikut:

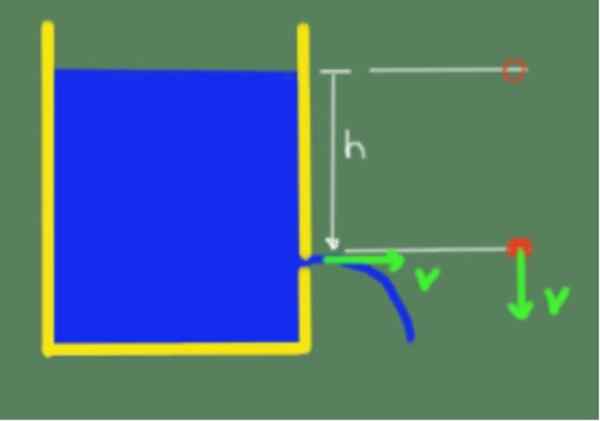Ilustrasi Teorema Torricelli. Sumber: Made sendiri.

Karena teorema Torricelli kita kemudian dapat mengatakan bahwa kecepatan output cairan oleh lubang yang setinggi h di bawah permukaan bebas cairan diberikan oleh formula berikut:

Di mana g adalah percepatan gravitasi dan h adalah ketinggian dari lubang ke permukaan bebas cairan.

Penginjil Torricelli adalah fisik dan ahli matematika yang lahir di kota Faenza, Italia pada 1608. Torricelli dikaitkan dengan penemuan Barometer Merkurius dan sebagai pengakuan ada unit tekanan yang disebut "Torr", setara dengan Mercury Milimeter (mm Hg).

Demonstrasi teorema

Dalam teorema Torricelli dan dalam formula yang memberikan kecepatan, ia mengasumsikan bahwa kerugian karena viskositas tercela, seperti pada jatuh bebas diasumsikan bahwa gesekan karena udara yang mengelilingi objek yang jatuh tidak signifikansional.

Asumsi sebelumnya masuk akal dalam banyak kasus dan juga menyiratkan konservasi energi mekanik.

Untuk menunjukkan teorema, pertama -tama kita akan menemukan rumus kecepatan untuk objek yang dilepaskan dengan kecepatan awal nol, dari ketinggian yang sama dengan permukaan cairan dalam tangki.

Dapat melayani Anda: gelombang tiga dimensi: konsep, jenis dan contoh

Prinsip konservasi energi akan diterapkan untuk mendapatkan kecepatan objek yang jatuh tepat ketika ketinggian telah turun H sama dengan yang dari lubang ke permukaan bebas.

Karena tidak ada kerugian gesekan, itu valid untuk menerapkan prinsip konservasi energi mekanik. Misalkan objek yang jatuh memiliki massa M dan tinggi H diukur dari tingkat output cairan.

Objek yang jatuh

Ketika objek dilepaskan dari ketinggian yang sama dengan permukaan bebas cairan, energinya hanya potensi gravitasi, karena kecepatannya nol dan, oleh karena itu, energi kinetiknya nol. EP energi potensial diberikan oleh:

EP = M G H

Ketika masuk di depan lubang tingginya adalah nol, maka energi potensial adalah nol, jadi hanya memiliki energi kinetik yang diberikan oleh:

Ec = ½ m v²

Karena energi dipertahankan EP = EC dari apa yang diperoleh:

½ m v² = m g h

Membersihkan kecepatan v Formula Torricelli kemudian diperoleh:

Cairan yang keluar dari lubang

Selanjutnya kita akan menemukan kecepatan output cairan melalui lubang, untuk menunjukkan bahwa itu bertepatan dengan yang hanya dihitung untuk objek yang jatuh dengan bebas.

Untuk ini kami akan mengandalkan prinsip Bernoulli, yang tidak lebih dari konservasi energi yang diterapkan pada cairan.

Prinsip Bernoulli dirumuskan seperti ini:

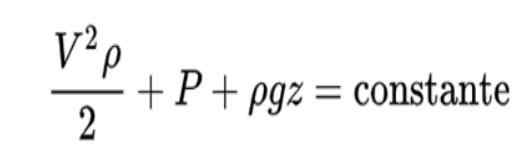
Interpretasi formula ini adalah sebagai berikut:

• Istilah pertama mewakili energi kinetik cairan per unit volume
• Yang kedua mewakili pekerjaan yang dilakukan oleh tekanan per unit area melintang
• Yang ketiga mewakili energi potensial gravitasi per unit volume cairan.

Dapat melayani Anda: kecepatan instan: definisi, formula, perhitungan dan latihan

Ketika kita mulai dari premis yang merupakan cairan yang ideal, dalam kondisi non -turbulen dengan kecepatan yang relatif rendah, maka berkaitan dengan menegaskan bahwa energi mekanik per satuan volume dalam fluida konstan di semua daerah atau bagian transversal yang sama.

Dalam formula ini V adalah kecepatan cairan, ρ Kepadatan cairan, P tekanan dan z Posisi vertikal.

Pada gambar yang muncul di bawah ini, formula Torricelli ditunjukkan berdasarkan prinsip Bernoulli.

Kami menerapkan formula Bernoulli pada permukaan bebas cairan yang kami tunjukkan untuk (1) dan di lubang output yang kami tunjukkan oleh (2). Level tinggi nol telah dipilih dengan lubang output.

Di bawah premis bahwa penampang dalam (1) jauh lebih besar daripada di (2), kita kemudian dapat mengasumsikan bahwa kecepatan penurunan cairan dalam (1) secara praktis diabaikan.

Inilah sebabnya V telah ditempatkan₁= 0, tekanan yang menjadi sasaran cairan dalam (1) adalah tekanan atmosfer dan tinggi yang diukur dari lubang H.

Untuk bagian output (2) kami mengasumsikan bahwa kecepatan output adalah V, tekanan di mana cairan ke outlet juga dikenakan adalah tekanan atmosfer dan tinggi output nol.

Nilai yang sesuai dengan bagian (1) dan (2) diganti dalam rumus Bernoulli dan sama. Kesetaraan valid karena kami berasumsi bahwa cairan itu ideal dan tidak ada kerugian gesekan kental. Setelah semua istilah telah disederhanakan, kecepatan diperoleh di lubang output.

Dapat melayani Anda: Dwarf merah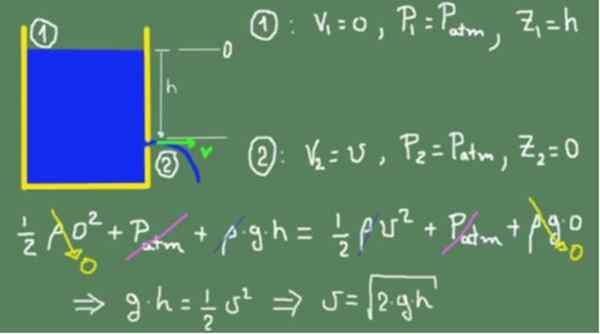

Kotak sebelumnya menunjukkan bahwa hasil yang diperolehnya sama dengan objek yang jatuh dengan bebas,

Dengan apa yang ditunjukkan prinsip torricelli.

Latihan terpecahkan

Latihan 1

yo) Tabung outlet kecil dari tangki air adalah 3 m di bawah permukaan air. Hitung kecepatan outlet air.

Larutan:

Gambar berikut menunjukkan bagaimana formula Torricelli diterapkan pada kasus ini.

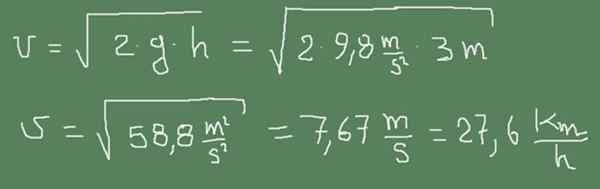
Latihan 2

Ii) Dengan asumsi bahwa tabung output dari tangki latihan sebelumnya memiliki diameter 1 cm, hitung aliran outlet air.

Larutan:

Aliran adalah volume cairan yang keluar per unit waktu, dan hanya dihitung dengan mengalikan area lubang output dengan kecepatan output.

Gambar berikut menunjukkan detail perhitungan.

Latihan 3

AKU AKU AKU) Tentukan seberapa tinggi permukaan air bebas dalam wadah jika diketahui

yang ada di lubang di bagian bawah wadah, air datang ke 10 m/s.

Larutan:

Bahkan ketika lubang berada di bagian bawah wadah, formula Torricelli dapat diterapkan.

Gambar berikut menunjukkan detail perhitungan.

Referensi

1. Wikipedia. Teorema Torricelli.
2. Hewitt, hlm. Ilmu Fisik Konseptual. Edisi Kelima.119.
3. Muda, Hugh. 2016. Fisika Universitas Sears-Zansky dengan Fisika Modern. Edisi ke -14. Pearson. 384.