Teorema binomial

Apa teorema binomial?

Dia Teorema binomial Ini adalah persamaan yang memberi tahu kita bagaimana ekspresi bentuk berkembang (a+b)^N Untuk beberapa bilangan alami n. Binomial tidak lebih dari jumlah dua elemen, seperti (a+b). Itu juga memungkinkan kita untuk mengetahui istilah yang diberikan oleh^kB^N-K Apa koefisien yang menyertainya.

Teorema ini umumnya dikaitkan dengan penemu bahasa Inggris, fisik dan matematikawan Sir Isaac Newton; Namun, berbagai catatan telah ditemukan yang menunjukkan bahwa keberadaannya sudah dikenal di Timur Tengah, sekitar tahun 1000.

Nomor kombinasi

Teorema binomial secara matematis memberi tahu kita hal berikut:

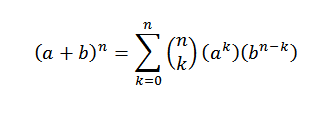
Dalam ungkapan ini A dan B adalah bilangan real dan n adalah angka alami.

Sebelum memberikan demonstrasi, mari kita lihat beberapa konsep dasar yang diperlukan.

Nomor kombinatorial atau kombinasi N dalam k dinyatakan sebagai berikut:

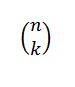
Ini mengungkapkan nilai berapa banyak subset dengan elemen k dapat dipilih dari satu set elemen n. Ekspresi aljabar -nya diberikan oleh:

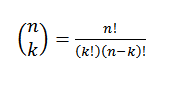
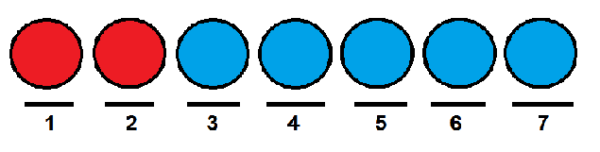
Mari kita lihat contoh: Misalkan kita memiliki sekelompok tujuh bola, yang dua di antaranya berwarna merah dan sisanya biru.

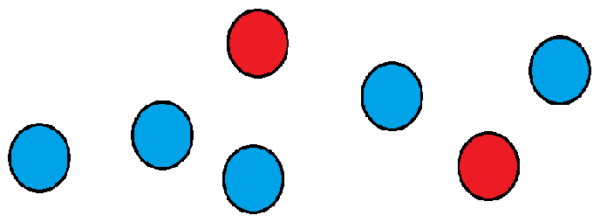
Kami ingin tahu berapa banyak cara kami dapat memesannya berturut -turut. Salah satu caranya adalah menempatkan dua merah di posisi pertama dan kedua, dan sisa bola di posisi yang tersisa.

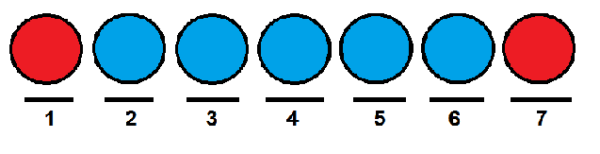
Mirip dengan kasus sebelumnya, kita bisa memberikan bola merah masing -masing posisi pertama dan terakhir, dan menempati yang lain dengan bola biru.

Sekarang, cara yang efektif untuk menghitung berapa banyak cara kita dapat memesan bola berturut -turut menggunakan nomor kombinatorial. Kita dapat melihat setiap posisi sebagai elemen dari set berikut:

Dapat melayani Anda: angka sempurna: cara mengidentifikasi mereka dan contoh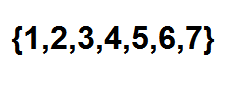

Di bawah ini hanya untuk memilih subset dari dua elemen, di mana masing -masing elemen ini mewakili posisi yang akan ditempati bola merah. Kita dapat melakukan pilihan ini sesuai dengan hubungan yang diberikan oleh:

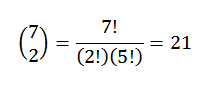
Dengan cara ini, kita memiliki bahwa ada 21 cara untuk memesan bola seperti itu.

Gagasan umum dari contoh ini akan sangat berguna dalam demonstrasi teorema binomial. Mari kita lihat kasus tertentu: jika n = 4, kita memiliki (a+b)⁴, Itu tidak lebih dari:

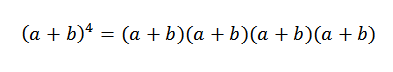
Ketika kami mengembangkan produk ini, kami memiliki jumlah istilah yang diperoleh dengan mengalikan elemen masing -masing dari empat faktor (A+B). Dengan demikian, kita akan memiliki istilah yang akan dalam bentuk:

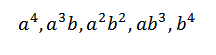
Jika kami ingin mendapatkan istilah formulir⁴, Hanya cukup untuk berlipat ganda sebagai berikut:

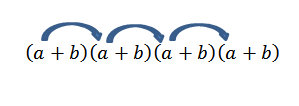
Perhatikan bahwa hanya ada satu cara untuk mendapatkan elemen ini; Tapi apa yang terjadi jika kita sekarang mencari akhir formulir²B²? Karena "A" dan "B" adalah bilangan real dan, oleh karena itu, itu sepadan dengan hukum komutatif, kita harus mendapatkan istilah ini adalah untuk berlipat ganda dengan anggota seperti yang ditunjukkan oleh panah.

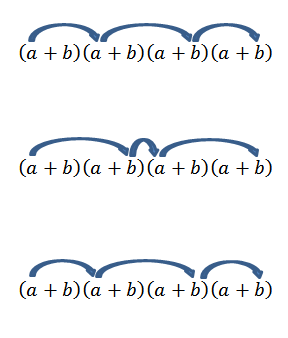
Melakukan semua operasi ini biasanya agak membosankan, tetapi jika kita melihat istilah "A" sebagai kombinasi di mana kita ingin tahu berapa banyak cara kita dapat memilih dua "a" dari satu set empat faktor, kita dapat menggunakan gagasan tentang Contoh sebelumnya dari contoh sebelumnya. Jadi, kami memiliki yang berikut:

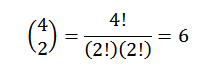
Dengan demikian, kita tahu bahwa dalam pengembangan akhir ekspresi (A+B)⁴ Kami akan memiliki tepat ke -6²B². Menggunakan ide yang sama untuk elemen lain, Anda harus:

Dapat melayani Anda: Angka transenden: Apa itu, formula, contoh, latihan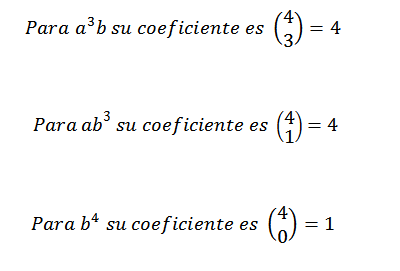

Kemudian kami menambahkan ekspresi yang diperoleh di atas dan kami harus:

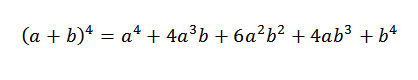
Ini adalah demonstrasi formal untuk kasus umum di mana "n" adalah angka alami.

Demonstrasi

Perhatikan bahwa istilah yang tersisa saat berkembang (A+B)^N Mereka dari formulir^kB^N-K, dimana k = 0,1, ..., n. Menggunakan ide contoh sebelumnya, kami memiliki cara untuk memilih variabel "k" "A" dari faktor "n" adalah:

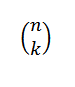
Saat memilih dengan cara ini, kami secara otomatis memilih variabel N-K "B". Ini mengikuti itu:

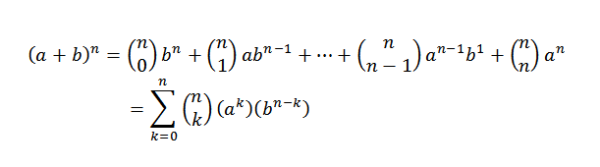
Contoh

Mempertimbangkan (a+b)⁵, Apa yang akan menjadi perkembangan Anda?

Untuk teorema binomial kita harus:

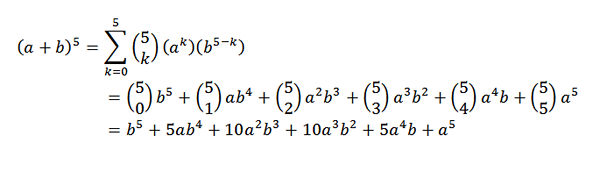
Teorema binomial sangat berguna jika kita memiliki ekspresi di mana kita ingin tahu apa koefisien istilah tertentu tanpa harus melakukan pengembangan lengkap. Sebagai contoh, kita dapat mengambil yang tidak diketahui berikut: apa koefisien x⁷Dan⁹ Dalam pengembangan (x + y)¹⁶?

Untuk teorema binomial, kita memiliki koefisiennya adalah:

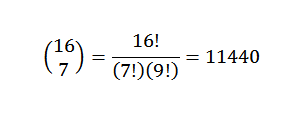
Contoh lain adalah: apa koefisien x⁵Dan⁸ Dalam pengembangan (3x-7y)¹³?

Pertama kami menulis ulang ekspresi dengan cara yang nyaman; ini:

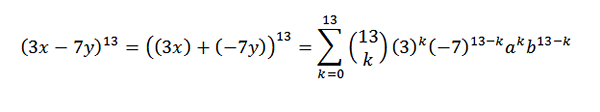
Kemudian, menggunakan teorema binomial, kami memiliki bahwa koefisien yang dicari adalah ketika Anda memiliki k = 5

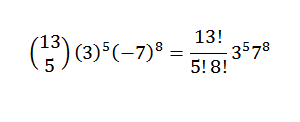
Contoh lain dari penggunaan teorema ini adalah dalam demonstrasi beberapa identitas umum, seperti yang akan kami sebutkan di bawah ini.

Identitas 1

Jika "n" adalah angka alami, kita harus:

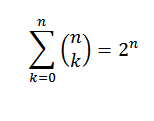
Untuk demonstrasi kami menggunakan teorema binomial, di mana "A" dan "B" mengambil nilai 1. Lalu kita memiliki:

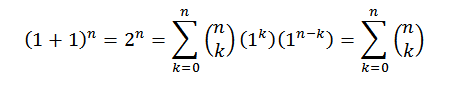
Dengan cara ini kami telah membuktikan identitas pertama.

Dapat melayani Anda: pilihan acak dengan atau tanpa penggantian

Identitas 2

Jika "n" adalah angka alami, maka

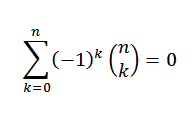
Untuk teorema binomial kita harus:

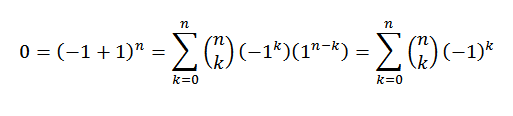
Demonstrasi lain

Kita dapat membuat demonstrasi yang berbeda untuk teorema binomial menggunakan metode induktif dan identitas Pascal, yang memberi tahu kita bahwa, jika "n" dan "k" adalah bilangan bulat positif yang memenuhi n ≥ k, lalu: lalu:

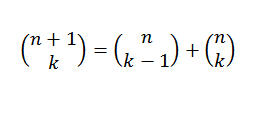
Demonstrasi induksi

Mari kita lihat bahwa basis induktif terpenuhi.  Jika n = 1, kita harus:

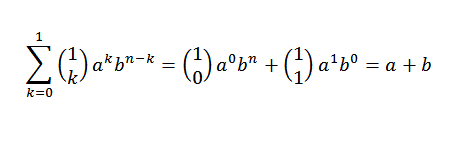
Memang, kita melihat bahwa itu terpenuhi. Sekarang, baik n = j sehingga terpenuhi:

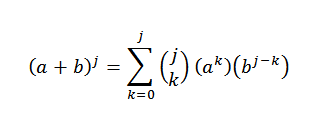
Kami ingin melihat bahwa untuk n = j+1 memang benar bahwa:

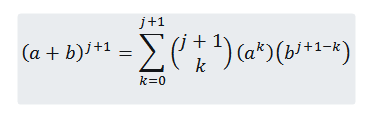
Jadi kita harus:

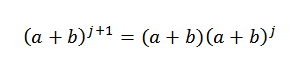
Dengan hipotesis kita tahu itu:

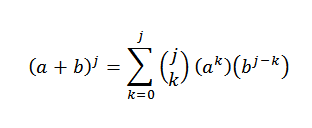
Kemudian, menggunakan properti distributif:

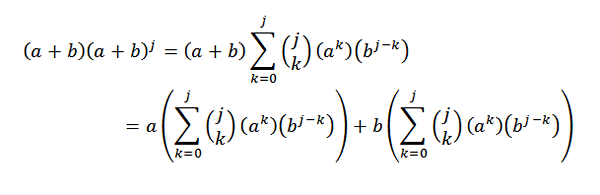
Selanjutnya, mengembangkan masing -masing ringkasan adalah:

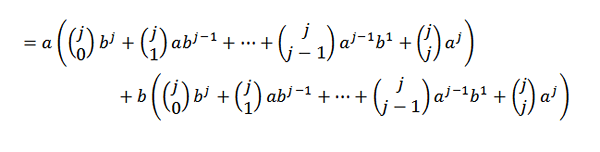
Sekarang, jika kita mengelompokkan dengan nyaman, kita harus:

Menggunakan identitas Pascal, kita harus:

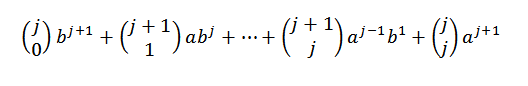
Akhirnya, perhatikan bahwa:

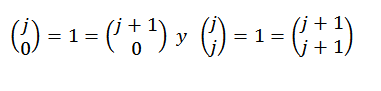
Oleh karena itu, kita melihat bahwa teorema binomial dipenuhi untuk setiap "n" milik bilangan alami, dan dengan ini uji berakhir.

Keingintahuan

Nomor kombinatorial (NK) juga disebut koefisien binomial karena justru koefisien yang muncul dalam pengembangan binomial (A+B)^N.

Isaac Newton memberikan generalisasi teorema ini untuk kasus di mana eksponen adalah bilangan real; Teorema ini dikenal sebagai Teorema Binomial Newton.

Sudah di Antiquity Hasil ini dikenal untuk kasus tertentu di mana n = 2. Kasus ini disebutkan di Item Euclid.