Jenis fungsi dan grafiknya

Ada beragam Jenis fungsi yang digunakan untuk memodelkan masalah dalam cabang pengetahuan seperti ilmu alam, administrasi, ekonomi dan ilmu sosial. Secara matematis, fungsi adalah hubungan antara dua atau lebih variabel.

Sering kali, objek atau jumlah tertentu saling terkait. Jumlah ini diwakili oleh variabel. Misalnya, ada dua variabel terkait, milik dua set A dan B, tidak harus numerik, meskipun sebagian besar waktu mereka-.

Untuk dianggap sebagai fungsi, hubungan ini harus memenuhi dua kondisi: yang pertama adalah bahwa semua elemen set awal untuk berpartisipasi, dan yang kedua, bahwa setiap elemen set tersebut terkait dengan hanya satu elemen set B B.

Variabel biasanya dipanggil dengan huruf X Dan Dan, dengan X sebagai variabel bebas Dan Dan sebagai variabel tak bebas. Secara alami, mereka dapat dipanggil dengan cara lain, memilih nama variabel sesuai dengan besarnya.

Hubungan antara keduanya dilambangkan melalui surat itu F -atau huruf lain dari alfabet-, dan diwakili dalam beberapa cara, seperti satu set pasangan yang dipesan, grafik, ekspresi verbal atau formula aljabar:

• f (x) = x + 1
• Populasi P kota tertentu dalam interval waktu tertentu t.
• H (x) = (1,3); (2,4); (3,5); (4.6)

Fungsi ditandai dengan memiliki domain Dan jangkauan atau rute. Domain adalah himpunan nilai yang variabel X Anda dapat mengambil, sedangkan rentang adalah himpunan nilai yang memperoleh fungsi atau variabel dependen dan.

Klasifikasi fungsi

Fungsi dapat dikelompokkan ke dalam 5 kategori besar, sebagaimana tercermin dalam skema berikut, di mana masing -masing kelompok diberi label dengan nomor Romawi dan warna. Mulai dari kiri ke kanan, fungsi diklasifikasikan menurut:

• I) bentuknya.
• Ii) Simetri.
• Iii) cara untuk mengekspresikan variabel.
• Iv) kesinambungan dan monotonnya.
• V) Cara di mana elemen domain terkait dengan rentang.

Kriteria klasifikasi utama untuk fungsi. Sumber: f. Zapata.

Sekarang ikuti deskripsi singkat tentang masing -masing jenis fungsi dengan contoh masing -masing.

I) berfungsi sesuai bentuknya

yo.1) Fungsi Aljabar

Mereka adalah salah satu fungsi yang paling banyak digunakan di berbagai bidang sains, dan oleh karena itu mereka adalah yang paling terkenal. Mereka ditandai dengan memiliki aturan korespondensi, ekspresi aljabar.

Pada gilirannya, fungsi aljabar dibagi lagi menjadi jenis berikut:

• yo.1.a) polinomial atau polinomial.
• yo.1.b) rasional.
• yo.1.c) tidak rasional.
• yo.1.d) pada bagian.

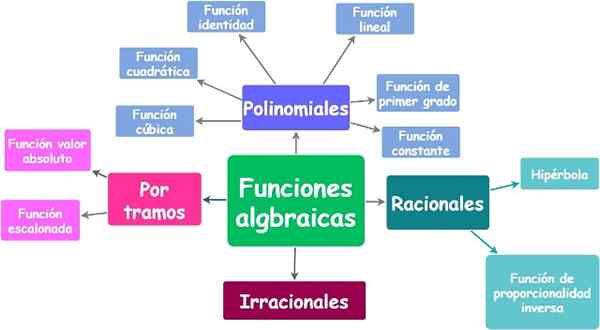Fungsi aljabar dan jenisnya. Sumber: f. Zapata.

yo.1.a) Fungsi polinomial atau polinomial

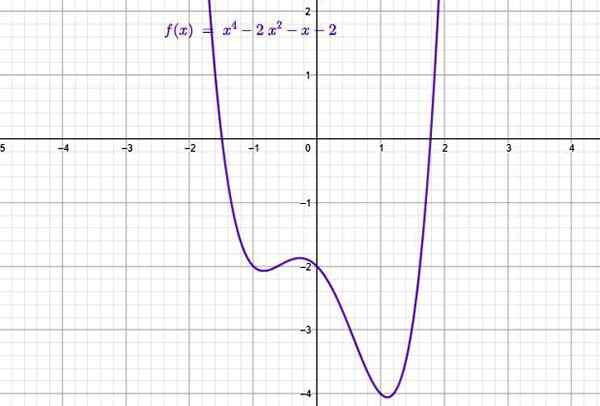Contoh fungsi tipe polinomial. Sumber: f. Zapata melalui Geogebra.

Mereka terdiri dari jumlah istilah yang bentuk umumnya adalah:

P (x) = a_NX^N + ke _N-1X^N-1 +… ke₁x + a₀

Dimana koefisiennya_N, ke _N-1… ke₁, ke₀ Mereka adalah bilangan real dan n adalah bilangan bulat. Domain fungsi polinomial adalah himpunan bilangan real dan juga merupakan fungsi berkelanjutan di seluruh domain itu.

Pada gambar atas adalah grafik dari fungsi polinomial berikut dari urutan 4:

f (x) = x⁴ - 2x² - x -2

Di antara fungsi polinomial, beberapa kasus tertentu dibedakan, sesuai dengan nilai -nilai koefisien. Perlu dipertimbangkan dengan cermat, karena mereka sangat berguna dalam berbagai situasi:

i) fungsi konstan

Ada fungsi konstan ketika semua koefisien dibatalkan, kecuali₀:

f (x) = a₀ = k

Grafik fungsi konstan adalah garis lurus sejajar dengan sumbu horizontal, seperti garis:

• f (x) = 2
• g (x) = π
• H (x) = -3/2

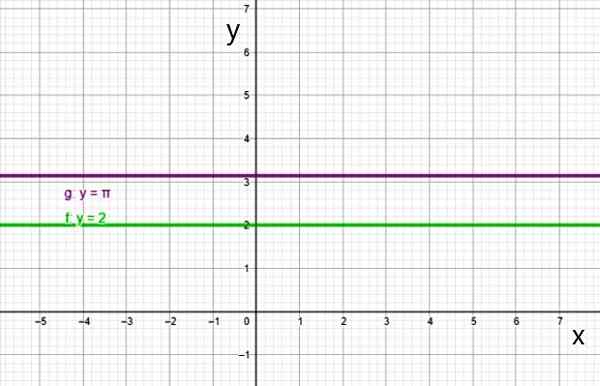Dua contoh fungsi konstan. Sumber: f. Zapata.

Ii) Fungsi Gelar Pertama

Fungsi -derajat pertama atau fungsi terkait adalah bahwa grafiknya adalah garis lurus. Ini adalah kasus khusus dari fungsi polinomial di mana semua koefisien annul₁ sudah₀. Itu diberikan oleh:

f (x) = a₁x + a₀

Nilainya a₁ Itu adalah kemiringan garis, yang memberikan ukuran kecenderungannya, dan₀ Itu adalah potongan garis dengan sumbu vertikal. Keduanya dapat mengambil nilai positif atau negatif.

Contoh fungsi derajat pertama adalah sebagai berikut:

• G (x) = 2x -1
• H (x) = -6x +5/2

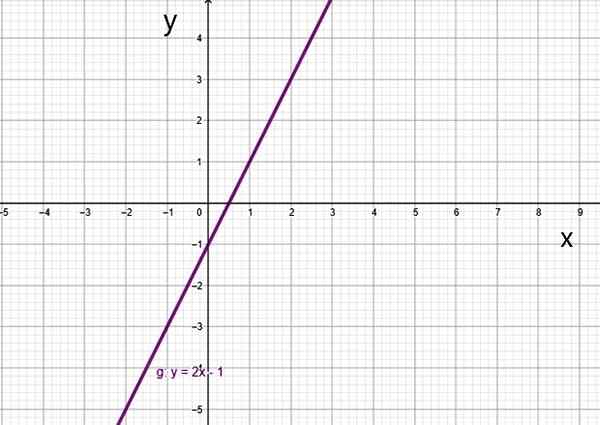Fungsi derajat pertama f (x) = 2x-1. Sumber: f. Zapata.

Ada kasus khusus, yang merupakan fungsi linier.

Dapat melayani Anda: Tindakan Kecenderungan Pusat untuk Data Pengelompokan: Rumus, Latihan

iii) fungsi linier

Saat koefisien₀ Ini adalah 0, fungsi selalu melewati asal dan diekspresikan oleh f (x) = a₁X, menelepon Funtion Lineal, Apa kabarmu:

• f (x) = 5x
• G (x) = -7x

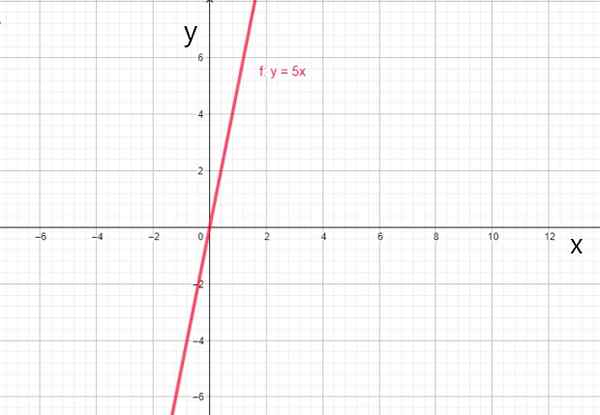Fungsi linier f (x) = 5x. Sumber: f. Zapata.

iv) Fungsi Identitas

Ini adalah kasus khusus dari fungsi linier, di mana₁ = 1:

f (x) = x

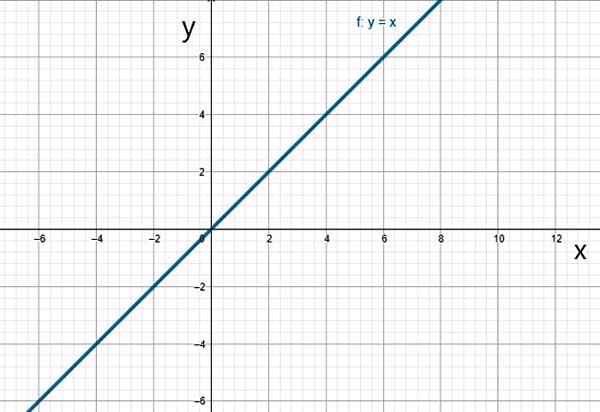Fungsi identitas. Sumber: f. Zapata.

v) Fungsi kuadratik

Itu memiliki bentuk umum:

f (x) = a₂X² +ke₁x + a₀

Dengan₂  ≠ 0.

Grafiknya adalah perumpamaan yang sumbu aksial atau simetri sejajar dengan sumbu ordinat. Selalu memotong sumbu vertikal pada titik koordinat x = 0, y = a₀. Sedangkan untuk persimpangan dengan sumbu horizontal, ini dapat mencapai maksimum 2.

Contoh fungsi kuadratik adalah:

• f (x) = x² - 3x - 4
• G (x) = 4x²
• H (x) = x²-1

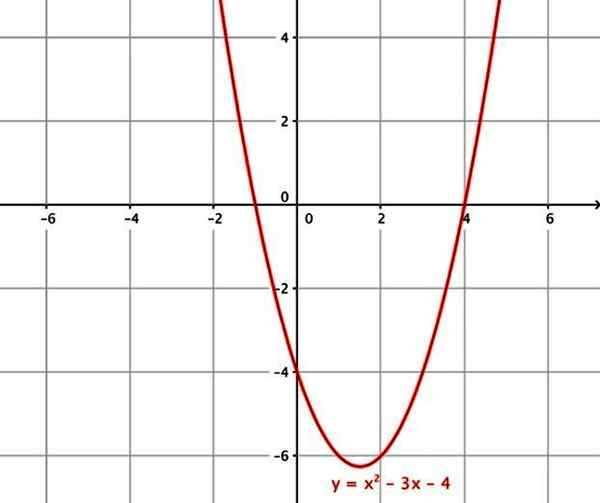Fungsi kuadratik. Sumber: Wikimedia Commons.

vi) fungsi kubik

Seperti namanya, fungsi kubik berisi kekuatan 3:

f (x) = a₃X³ + ke₂X² + ke₁x + a₀

Koefisien a₃ Itu selalu berbeda dari 0, seperti dalam kasus ini:

• f (x) = x³
• G (x) = 5x³ - 2
• H (x) = -3x³ + 4x² + 10x + 1

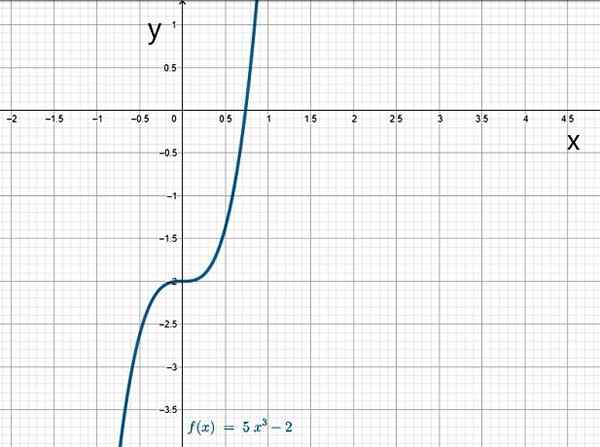Fungsi kubik. Sumber: f. Zapata.

yo.1.b) fungsi rasional

Fungsi rasional memiliki formulir:

 Di mana p (x) dan q (x) adalah polinomial yang tidak dapat direduksi, yaitu, mereka tidak memiliki faktor umum dan dalam kasus apa pun q (x) ≠ 0.

Dari domain fungsi rasional, semua nilai yang membatalkan denominator q (x), yaitu akarnya, sedangkan nilai -nilai nilai nilai -nilai dari Dan yang menentukan asimtot horizontal.

Asimptot adalah garis yang mendekati fungsi, baik di sebelah kiri maupun di sebelah kanan, di atas atau di bawah, tetapi tidak pernah menyeberang. Garis seperti itu bisa vertikal, horizontal atau miring.

Contoh fungsi rasional adalah:

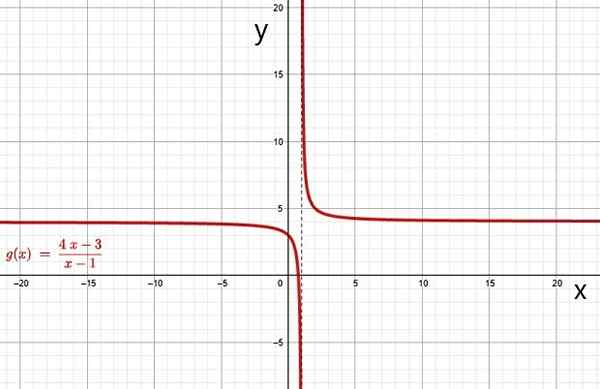Fungsi rasional. Sumber: f. Zapata melalui Geogebra.

i) Hiperbola

Grafik fungsi rasional adalah hiperbola saat polinomial dalam denominator Q (x) memiliki grade 1. Grafik fungsi f (x) dan g (x) dari contoh di atas adalah hiperbola, dapat dengan mudah diperiksa melalui perangkat lunak grafik online gratis, seperti Geogebra.

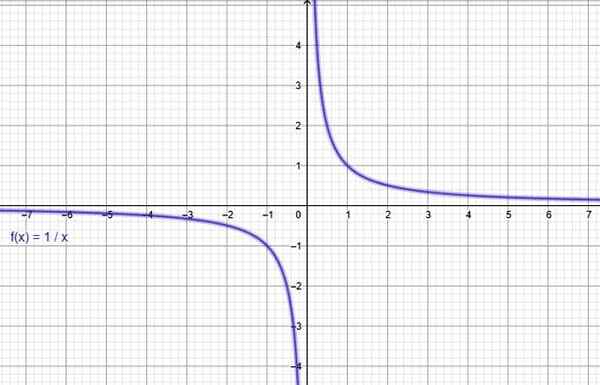Fungsi y = 1/x. Sumber: f. Zapata melalui Geogebra.

Ii) fungsi proporsionalitas terbalik

Ini adalah fungsi dari bentuk:

Dimana c adalah bilangan real yang berbeda dari 0. Domainnya adalah himpunan bilangan real kecuali untuk 0.

yo.1.c) fungsi irasional

Adalah mereka yang variabel independen berada di bawah tanda radikal. Bentuk umumnya adalah:

Beberapa fungsi ini bisa:

• 
• 

Domain fungsi -fungsi ini ditentukan sebagai berikut:

-Jika akarnya adalah indeks torsi, jumlah subradical f (x) harus selalu 0 atau positif.

-Saat akarnya aneh, f (x) bisa positif atau negatif. Oleh karena itu dalam hal ini domain fungsi adalah bilangan real.

Misalnya, domain:

Ini adalah himpunan bilangan real sehingga X-3 lebih besar dari atau sama dengan 0. Dalam hal ini, x harus lebih besar dari atau sama dengan 3. Oleh karena itu domain fungsi ini adalah himpunan nilai interval [3, ∞+).

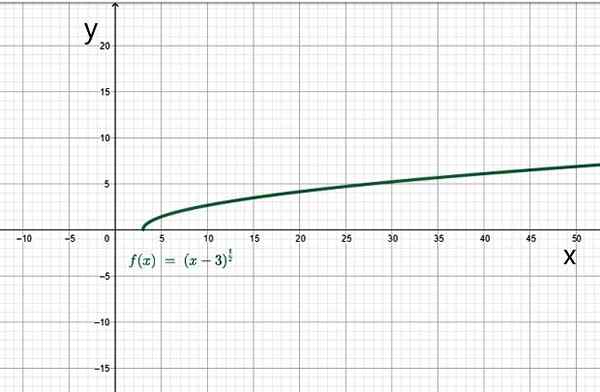 Contoh fungsi irasional. Sumber: f. Zapata.

yo.1.d) Fungsi berkeping -keping atau pada bagian

Fungsi di bagian, oleh bagian atau potongan adalah yang membutuhkan lebih dari satu rumus untuk nilai domain yang berbeda. Berikut adalah beberapa contoh aplikasi Anda:

-Tarif untuk mengirim paket melalui surat, tergantung pada berat atau volume, asal dan tujuan yang sama.

-Tarif untuk layanan, misalnya telepon dan listrik.

-Penjualan tiket untuk museum atau taman hiburan, tergantung pada usia.

Dalam bentuk matematika, fungsi di bagian dapat, misalnya:

Domain suatu fungsi di bagian tergantung pada definisinya. Pada contoh sebelumnya, domain adalah set yang dibentuk oleh: (-∞, -1) ∪ [1,+∞).

Fungsi nilai absolut. Sumber: f. Zapata melalui Geogebra.

Ii) Fungsi Escalonada

Grafik fungsi ini oleh bagian terdiri dari langkah -langkah, seperti yang dari tangga atau dapat memiliki ketinggian yang berbeda, tergantung pada cara fungsi ditentukan.

Ini dapat melayani Anda: Hipparco of Nicea: Biografi dan Kontribusi untuk Sains

Untuk ini, interval terbatas [a, b] dipilih yang berisi sejumlah diskontinuitas tertentu, yang disebut x_yo < x₁ < x₂ <… . x_N  Dan interval terbuka dipilih (x_yo , X_i+1) Untuk memberinya konstanta nilai s_yo, Dengan lompatan pada poin x_yo. Nilai S_yo Itu adalah ketinggian langkah yang dimaksud.

Contoh fungsi yang terhuyung -huyung adalah seluruh bagian, yang mengambil angka apa pun dan mengaitkannya dengan bilangan bulat berikut, baik secara berlebih atau secara default. Berikut ini adalah seluruh bagian:

[x] = (bilangan bulat yang lebih besar ≤ x)

Menurut fungsi ini, seluruh bagian 2.5 adalah:

[2.5] = (bilangan bulat yang lebih besar ≤ 2.5) = 2

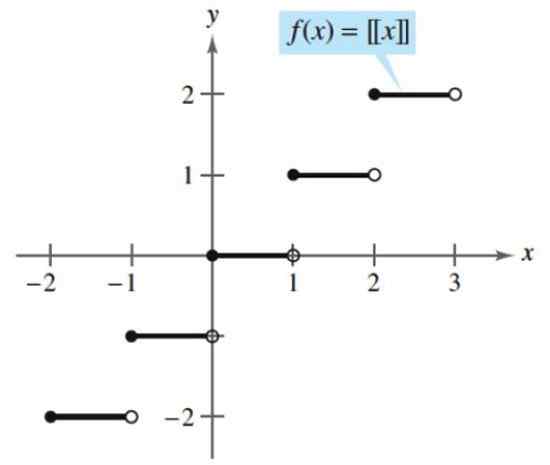Seluruh bagian dari. Sumber: Larson, R. Perhitungan dengan geometri analitik. McGraw-Hill.

yo.2) Fungsi transenden

Fungsi non -algebraic disebut transenden. Fungsi eksponensial, logaritmik dan trigonometri adalah fungsi transenden.

Di dalamnya variabelnya X Ini adalah bagian dari argumen fungsi atau sebagai bagian dari eksponen atau indeks beberapa root, misalnya:

• f (x) = log (x+1)
• H (x) = -0.2⋅8^-3x

Fungsi transenden memiliki banyak aplikasi, misalnya dalam studi getaran dan gelombang, distribusi probabilitas, pemodelan gelombang, pertumbuhan populasi yang beragam, peluruhan radioaktif, suku bunga dan banyak lagi. 

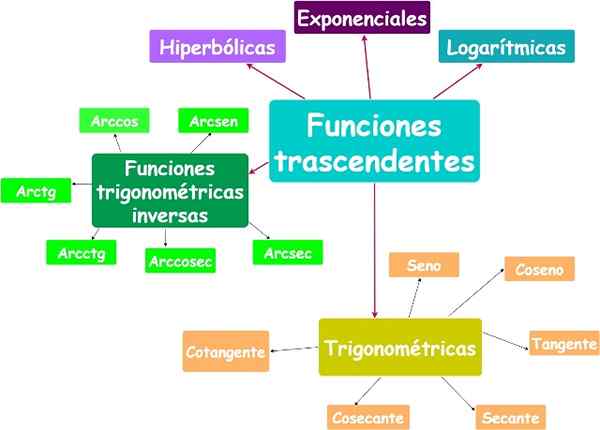Fungsi transenden utama. Sumber: f. Zapata.

yo.2.a) fungsi eksponensial 

Fungsi eksponensial ditentukan oleh:

f (x) = a^X

Di mana A adalah basis, yang selalu merupakan jumlah positif 1, dan variabel, bilangan real, muncul di eksponen. Secara umum, fungsi eksponensial ditulis:

f (x) = a⋅a^Bx

Di sini A dan B adalah koefisien nyata. Berikut ini adalah fungsi dari jenis ini:

• f (x) = 5e^X
• H (x) = 4. 10^5x
• g (t) = 8e^-2t

Basis Dan, Di mana Dan Itu adalah jumlah euler 2.71828 ..., sering muncul dalam masalah sains dan teknik, serta statistik. Saat fungsi memiliki basis ini dipanggil Fungsi eksponensial alami.

Domain fungsi eksponensial adalah himpunan bilangan real, sedangkan kisarannya adalah angka positif.

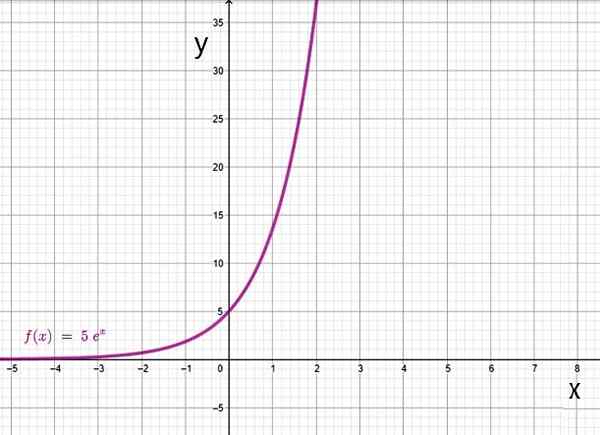Fungsi eksponensial berdasarkan. Sumber: f. Zapata melalui Geogebra.

yo.2.b) Fungsi logaritma

Untuk bagiannya, fungsi logaritma berdasarkan ke Ini adalah fungsi terbalik dari fungsi eksponensial berdasarkan ke. Ya:

catatan_ke x = y

Jadi:

x = a^Dan

Secara khusus, jika basis logaritma adalah angka E, fungsinya disebut Fungsi Logaritma Neperian Dan itu dilambangkan sebagai ln. Fungsi jenis ini adalah:

• f (x) = ln x
• g (x) = log (x+1)
• H (t) = 1 - log x²

Domain fungsi logaritma, terlepas dari basisnya, adalah bilangan real positif, tidak termasuk 0. Artinya, tidak ada logaritma angka negatif atau 0.

Namun, logaritma bisa 0 atau negatif: logaritma angka antara 0 dan 1 negatif dan untuk bagiannya mencapai_ke 1 = 0.

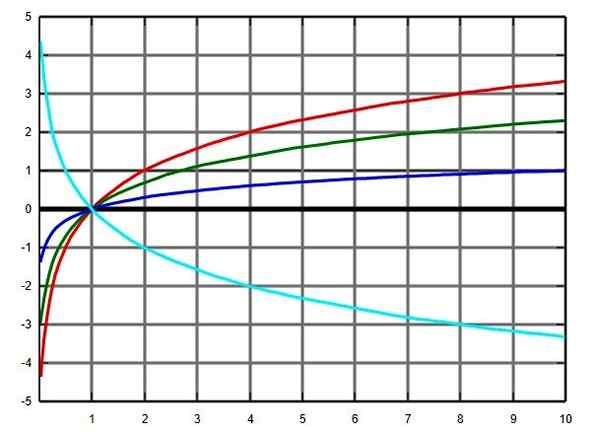Grafik Fungsi Logaritma di beberapa pangkalan: basis 2 dalam warna merah, hijau E, blue -base dan pirus di pangkalan 0.5. Sumber: Wikimedia Commons.

yo.2.c) fungsi trigonometri

Mereka adalah orang -orang yang berasal dari alasan trigonometri: sinus, kosinus, garis singgung, pengeringan, harmoning dan cotangent dari sudut x. Mereka dilambangkan masing -masing sebagai:

Sen x, cos x, tg x, sec x, bahaya x dan cotg x

Mereka adalah fungsi periodik, yang berarti bahwa bentuknya berulang, sehingga sangat berguna untuk menggambarkan fenomena alam seperti sinyal, osilasi, gerakan melingkar dan gerakan ayunan, yang ditandai dengan menjadi berulang.

Contoh fungsi trigonometri adalah:

• f (x) = sin x
• G (t) = 5⋅cos (ωt + π)
• H (x) = tg (x/2)

Variabel x diekspresikan dalam radianes.

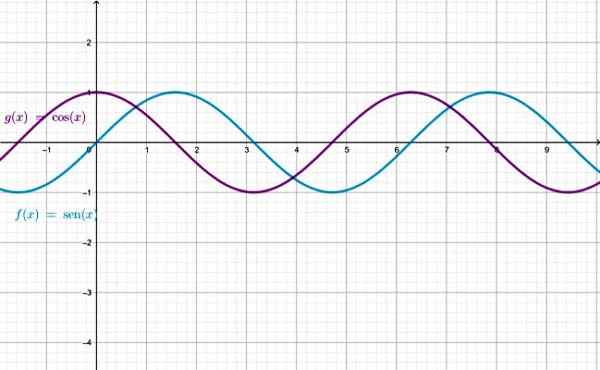Grafik fungsi sen x dan cos x, perhatikan bahwa mereka identik, kecuali bahwa satu dipindahkan sehubungan dengan yang lain. Sumber: f. Zapata melalui Geogebra.

Penguasaan Fungsi Sen X dan Cos X, adalah himpunan bilangan real. Untuk fungsi yang tersisa ada nilai x yang fungsi tidak ditentukan:

-Fungsi TG X tidak ada ketika x = ± π /2, ± 5π /2 ... Ini, semua kelipatan ganjil π /2.

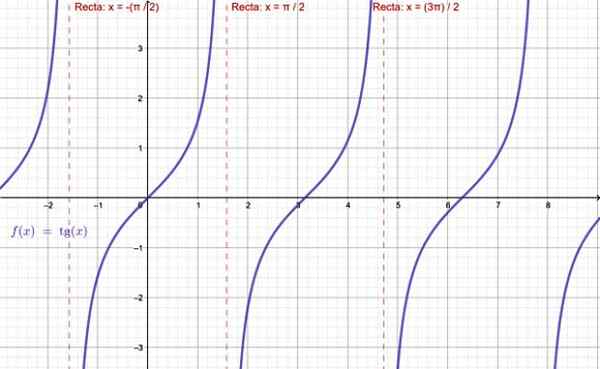Grafik fungsi garis singgung. Sumber: f. Zapata melalui Geogebra.

-Sedangkan untuk f (x) = cotg x, fungsi ini tidak didefinisikan untuk seluruh kelipatan π: ± π, ± 2π, ± 3π ..

Dapat melayani Anda: hukum tanda

-Fungsi y = sec x tidak valid ketika cos x = 0, yang tidak termasuk x = ± π /2, ± 5π /2… dari domainnya.

-Akhirnya, untuk f (x) = bahaya x, seluruh kelipatan π bukan milik domain mereka.

yo.2.d) Fungsi hiperbolik

Fungsi hiperbolik adalah kombinasi khusus dari eksponensial dan^X dan e^-X Dan mereka disebut sebagai dada, coseno .. .hiperbolis. Seperti halnya fungsi trigonometri, juga disebut "melingkar", ada 6 fungsi hiperbolik:

-Sinus hiperbolik Senh X:

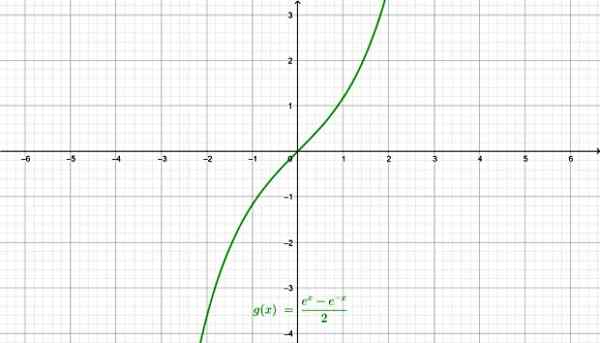Fungsi sinus hiperbolik. Sumber: f. Zapata melalui Geogebra.

-Cosinus hiperbolik Cosh x:

 -Tangen hiperbolik Tanh X:

 -Harvester Hiperbolik CSCH X:

 -Secant Hiperbolik Sech X:

-Cotangent hiperbolik COTH X:

Kabel fleksibel, terbuat dari bahan seragam dan gantung di antara dua titik, mengambil bentuk kurva yang disebut yg berhubung dgn deretan, yang diekspresikan sebagai cosinus hiperbolik:

yo.2.e) Fungsi trigonometri terbalik

Mereka sesuai dengan kebalikan dari fungsi trigonometri. Misalnya, apa yang akan menjadi sudut (busur) yang dadanya bernilai 0.5?

Jawabannya adalah arc sen 0.5, yang bertuliskan “Sinus dari 0.5 ”, dan sudut ini 30º, meskipun pada prinsipnya, ini bukan satu -satunya sudut yang bernilai 0.5, karena fungsi sen x bersifat periodik. Apa yang terjadi adalah bahwa jika fungsi Sen X diambil di seluruh domainnya, ia tidak akan memiliki kebalikan, sehingga fungsi arcoseno tidak dapat ditentukan. Masalah ini diselesaikan dengan membatasi segalanya pada sudut antara -π/2 dan +π/2.

Ini dapat dinyatakan sebagai berikut:

Jika Arc sen x = θ, itu berarti dosa θ = x

Dengan -π/2 ≤ θ ≤ π/2.

Notasi lain yang digunakan untuk arc sen x adalah f (x) = dosa^-1 X. Grafik ditampilkan di bawah ini:

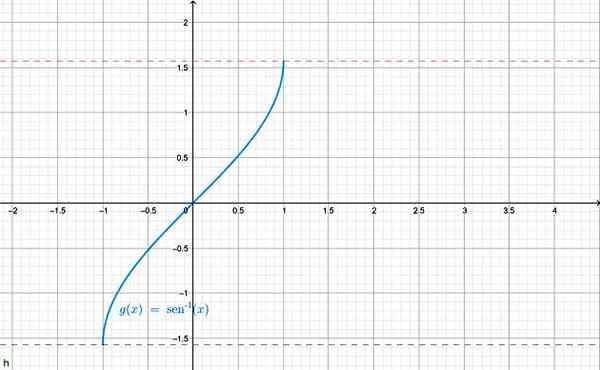Grafis fungsi arcsen x. Sumber: f. Zapata melalui Geogebra.

Dimungkinkan juga untuk mendefinisikan terbalik untuk fungsi trigonometri lainnya, misalnya: busur cos x = θ dan dengan demikian. Untuk masing -masing peringkat dibatasi dengan benar, menjadi kebalikan dari fungsi trigonometri yang sesuai.

Ii) Fungsi sesuai dengan simetrinya

Ii.1) par

Jika untuk semua x milik domain f (x) dipenuhi bahwa:

f (x) = f (-x)

Dikatakan bahwa fungsinya bahkan, seperti yang mengikuti:

• f (x) = x² - 3
• g (x) = cos x
• 

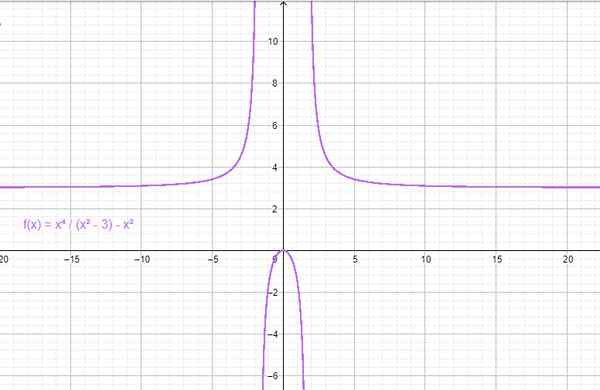  Contoh fungsi pasangan. Sumber: f. Zapata melalui Geogebra.

Misalnya, melakukan x = 1 di f (x) = x² - 3 diperoleh:

f (1) = 1² - 3 = -2.

Dan jika x = -1, lalu:

f (-1) = (-1)² - 3 = -2.

Kedua hasilnya identik.

Fungsi genap memiliki simetri di sekitar sumbu vertikal, seperti yang dapat dilihat pada gambar sebelumnya.

Ii.2) Fungsi ganjil

Di sisi lain, ya:

f (-x) = -f (x)

Fungsinya aneh.

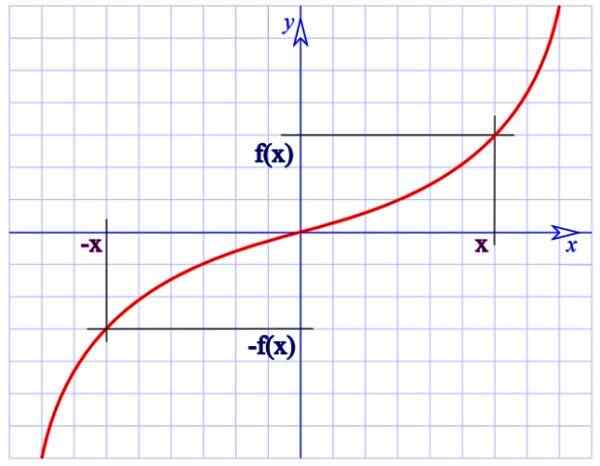Fungsi yang aneh. Sumber: Wikimedia Commons.

Misalnya fungsi f (x) = 1/x dari gambar atas ganjil, karena karena:

f (-x) = -1/x

DAN

-f (x) = -1/x

Fungsi impar penting lainnya adalah f (x) = sin x.

Perhatikan bahwa fungsi ganjil memiliki simetri rotasi 180º di sekitar asalnya (grafik tidak diubah jika setiap titik diubah 180º sehubungan dengan asal koordinat).

Iii) berfungsi sesuai dengan ekspresi variabel

AKU AKU AKU.1) Fungsi eksplisit

Mereka diekspresikan secara langsung dalam hal variabel dependen seperti y = f (x). Misalnya:

• f (x) = x³

AKU AKU AKU.2) Fungsi implisit

Dalam fungsi implisit, tidak ada variabel yang tampak jelas. Mereka dinyatakan sebagai f (x, y) = 0, seperti:

• X² + Dan² -3xy = 0
• xy = - x²+ X-5

Fungsi yang dijelaskan di seluruh artikel ini adalah fungsi eksplisit.

Iv) Fungsi sesuai dengan grafik Anda

Menurut grafik mereka, fungsinya bisa kontinu atau terputus. Fungsi berkelanjutan dapat dilacak tanpa mengganggu stroke, di sisi lain, fungsi -fungsi terputus -putus hadir. Pada gambar berikut, fungsinya terputus pada x = a:

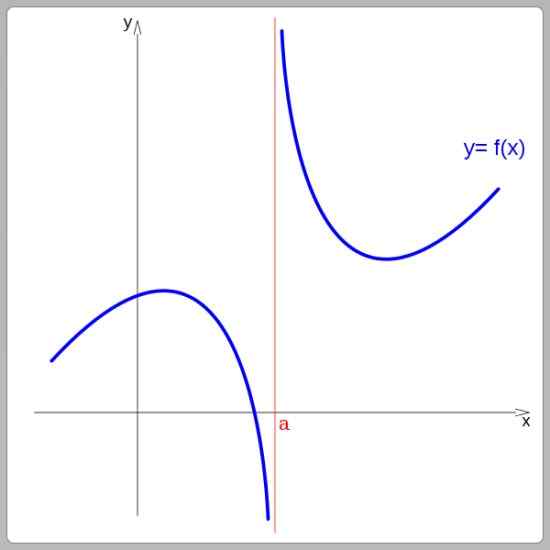Fungsi diskontinuitas pada x = a. Sumber: Wikimedia Commons.

Contoh fungsi kontinu adalah fungsi linier, fungsi kuadratik dan fungsi sinus dan kosinus. Dan di antara fungsi yang terputus adalah fungsi yang terhuyung -huyung dan fungsi tangen.

V) Fungsi sesuai dengan hubungan antara unsur -unsur domain dan jangkauan

V.1) Fungsi suntikan

Suatu fungsi adalah Suntikan Ketika tidak ada dua elemen berbeda dalam set start atau domain, yang memiliki gambar yang sama dalam set kedatangan.

Misalkan fungsi nyata memiliki, kecuali ditentukan lain, misalnya:

f (x) = 5x -2

Semua nilai x milik domain f (x), yang merupakan himpunan ℛ bilangan real, memiliki gambar yang unik dan nyata juga. Di sisi lain, dalam fungsi lain ini:

g (x) = x²

Ada berbagai elemen dalam domain yang memiliki gambar yang sama, misalnya x₁= 2 dan x₂= -2:

G (2) = g (-2) = 4.

Cara untuk mengidentifikasi fungsi injeksi dari grafiknya adalah menggambar garis horizontal, jika dipotong ke kurva pada lebih dari satu titik, fungsinya tidak -sjective.

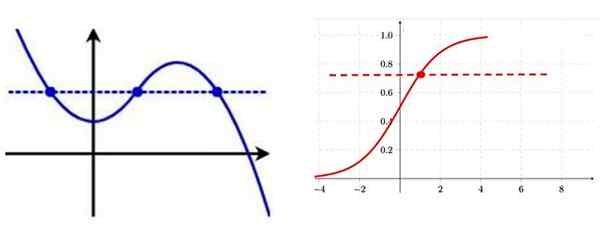Di sebelah kiri fungsi suntikan yang tidak, perhatikan bahwa ada beberapa titik grafik dengan koordinat vertikal yang sama. Di sebelah kanan fungsi injeksi, pada masing -masing titik kurva ia memiliki koordinat "y" tertentu. Sumber: f. Zapata.

V.2) fungsi berlebihan

Dalam Fungsi Onjective, Semua elemen set kedatangan adalah gambar dari beberapa elemen dari set awal. Contoh fungsi overjective adalah f (x) = 5x -2, tetapi g (x) = x yang sama² Bukan, karena nilai -nilai yang diambil g (x) hanyalah yang nyata yang nyata dan 0.

Namun, domain dapat didefinisikan ulang sehingga g (x) overjective, jika misalnya berubah menjadi semua yang nyata yang nyata ditambah 0. 

V.3) Fungsi Buta

Akhirnya, fungsi yang merupakan suntikan dan overjektif, disebut Bytyptive. Contoh fungsi buttive adalah: fungsi terkait, fungsi eksponensial dan fungsi logaritma.

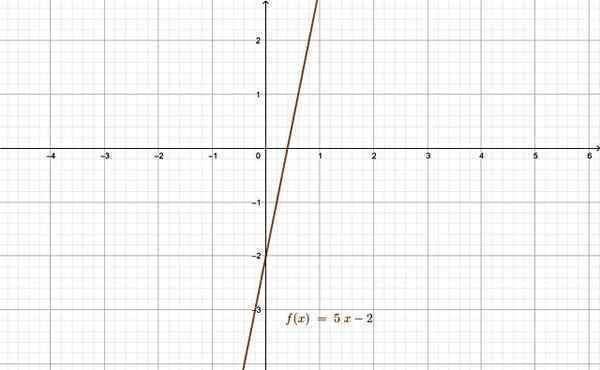Fungsi terkait adalah contoh yang baik dari fungsi Bijy. Sumber: f. Zapata melalui Geogebra.

Referensi

1. Zona e-math. Jenis fungsi. Pulih dari: emathzone.com.
2. Hoffman, J.G. Pemilihan masalah matematika. Ed. Spphinx.
3. Matematika itu menyenangkan. Referensi Fungsi Commons. Pulih dari: Mathisfun.com.
4. Requena, b. Rumus alam semesta. Jenis fungsi. Pulih dari: universoformulas.com.
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.