Karakteristik tembakan parabola, formula dan persamaan, contoh

Dia tembakan parabola Ini terdiri dari melempar objek atau proyektil dengan sudut tertentu dan membiarkannya bergerak di bawah aksi gravitasi. Jika resistensi udara tidak dipertimbangkan, objek, terlepas dari sifatnya, akan mengikuti lintasan dalam bentuk parabola.

Ini adalah gerakan sehari -hari, karena di antara olahraga yang paling populer adalah mereka di mana bola atau bola dilemparkan, baik dengan tangan, dengan kaki atau dengan instrumen seperti raket atau kelelawar misalnya.

Gambar 1. Jet air dari sumber hias mengikuti lintasan parabola. Sumber: Wikimedia Commons. Zátononyi Sandor (IFJ.), Fizped/cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0)

Untuk penelitian, tembakan parabola dipecah menjadi dua gerakan yang tumpang tindih: satu horizontal tanpa akselerasi, dan yang lain vertikal dengan akselerasi konstan ke bawah, yaitu gravitasi. Kedua gerakan memiliki kecepatan awal.

Katakanlah gerakan horizontal mengambil. Masing -masing gerakan ini tidak tergantung pada yang lain.

Mengingat fakta bahwa menentukan posisi proyektil adalah tujuan utama, perlu untuk memilih sistem referensi yang sesuai. Detailnya datang berikutnya.

[TOC]

Rumus dan persamaan tembakan parabola

Misalkan objek dilemparkan dengan sudut α sehubungan dengan kecepatan horizontal dan awal v_{salah satu} seperti yang ditunjukkan pada gambar di bawah ini ke kiri. Tembakan parabola adalah gerakan yang terjadi di pesawat Xy Dan dalam hal ini kecepatan awal terurai seperti ini:

v_sapi = v_{salah satu} cos α

v_Oy = v_{salah satu} dosa α

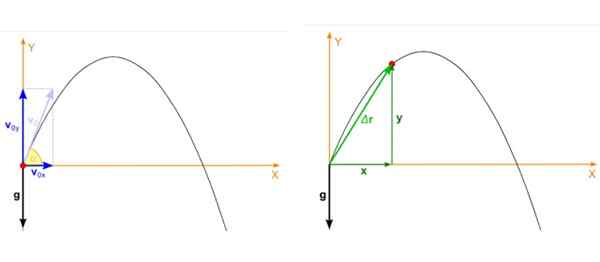Gambar 2. Di sebelah kiri kecepatan awal proyektil dan ke kanan posisi setiap saat peluncuran. Sumber: Wikimedia Commons. Zátononyi Sandor, (IFJ.) Fizped/CC BY-SA (https: // CreationCommons.Org/lisensi/by-sa/3.0).

Posisi proyektil, yang merupakan titik merah pada Gambar 2, gambar kanan, juga memiliki dua komponen yang bergantung pada waktu, satu dalam X Dan yang lainnya di Dan. Posisi adalah vektor yang dilambangkan sebagai R dan unitnya panjangnya.

Dapat melayani Anda: isomeria

Pada gambar, posisi awal proyektil bertepatan dengan asal sistem koordinat, oleh karena itu x_{salah satu} = 0, dan_{salah satu} = 0. Ini tidak selalu terjadi, asalnya dapat dipilih di mana saja, tetapi pilihan ini sangat menyederhanakan perhitungan.

Adapun dua gerakan dalam x dan y, ini adalah:

-X (T): Ini adalah gerakan lubur seragam.

-dan (t): sesuai dengan gerakan bujursangkar yang dipercepat secara seragam dengan G = 9.8 m/s² dan menunjuk ke bawah secara vertikal.

Dalam bentuk matematika:

x (t) = v_{salah satu} cos α.T

dan (t) = v_{salah satu} .dosa α.T - ½g.T²

Vektor posisi tetap:

R (t) = [v_{salah satu} cos α.T]yo + [v_{salah satu} .dosa α.T - ½g.T²] J

Dalam persamaan ini, pembaca yang penuh perhatian akan melihat bahwa tanda minus disebabkan oleh fakta bahwa keparahan menunjuk ke tanah, indra yang dipilih sebagai negatif, sementara itu dianggap positif.

Karena kecepatan adalah yang pertama berasal dari posisi, itu cukup untuk diturunkan R (t) tentang waktu dan dapatkan:

v (t) = v_{salah satu} cos α yo + (v_{salah satu} .dosa α - GT) J

Akhirnya akselerasi dinyatakan secara vektor sebagai:

ke (t) = -g J

- Lintasan, tinggi maksimum, waktu maksimum dan jangkauan horizontal

Lintasan

Untuk menemukan persamaan eksplisit lintasan, yang merupakan kurva y (x), Anda harus menghilangkan parameter waktu, membersihkan persamaan untuk x (t) dan mengganti dalam y (t). Penyederhanaan agak melelahkan, tetapi akhirnya diperoleh:

Tinggi maksimum

Tinggi maksimum terjadi saat v_Dan = 0. Mengetahui bahwa ada hubungan selanjutnya antara posisi dan kuadrat kecepatan:

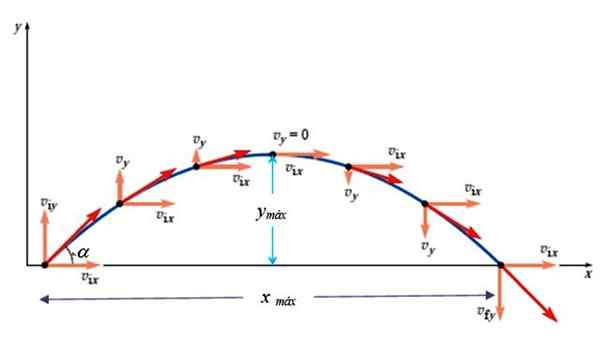Gambar 3. Kecepatan tembakan parabola. Sumber: Giambattista, a. Fisika.

v_Dan² = v_Oy ²- 2gy

Sedang mengerjakan v_Dan = 0 tepat ketika mencapai ketinggian maksimum:

0 = v_Oy ²- 2 g.Dan_Max → dan_Max = v_Oy ²/2 g

Dengan:

Dapat melayani Anda: akselerasi sentripetal: definisi, rumus, perhitungan, latihan

v_Oy = v_{salah satu} senα

Waktu maksimum

Waktu maksimum adalah waktu yang dibutuhkan objek untuk mencapai dan_Max. Untuk menghitungnya digunakan:

v_Dan = v_{salah satu} .dosa α - GT

Mengetahui bahwa v_Dan Itu dilakukan 0 saat t = t_Max, hasil:

v_{salah satu} .dosa α - G.T_Max = 0

T_Max = v_Oy /G

Rentang horizontal maksimum dan waktu penerbangan

Lingkupnya sangat penting, karena menunjukkan di mana objek akan jatuh. Jadi kita akan tahu apakah itu memberi putih atau tidak. Untuk menemukannya kita membutuhkan waktu penerbangan, total waktu atau t_v.

Dari ilustrasi sebelumnya, mudah untuk menyimpulkan itu T_v = 2.T_Max. Tetapi perhatian hanya benar jika peluncuran berada di level, yaitu, ketinggian titik awal sama dengan ketinggian kedatangan. Kalau tidak, waktu memecahkan persamaan tingkat kedua yang dihasilkan dari mengganti posisi akhir Dan_terakhir:

Dan_terakhir = v_{salah satu} .dosa α.T_v - ½g.T_v²

Bagaimanapun, ruang lingkup horizontal maksimum adalah:

X_Max = v_sapi. T_v

Contoh penembakan parabola

Tembakan parabola adalah bagian dari pergerakan manusia dan hewan. Juga dari hampir semua olahraga dan permainan di mana gravitasi mengintervensi. Misalnya:

Penembakan parabola dalam aktivitas manusia

-Batu itu dilemparkan oleh ketapel.

-Tendangan gawang kiper.

-Bola yang melempar pitcher.

-Panah yang keluar dari lengkungan.

-Semua jenis lompatan

-Melempar batu.

-Senjata lemparan apa pun.

Gambar 4. Batu yang dilemparkan oleh ketapel dan bola patey di kotak finish adalah contoh tembakan parabola. Sumber: Wikimedia Commons.

Tembakan parabola di alam

-Air yang tumbuh dari jet alami atau buatan seperti sumber.

-Batu dan lava tumbuh dari gunung berapi.

-Bola yang memantul di trotoar atau batu yang melakukannya di atas air.

-Semua jenis hewan yang melompat: kanguru, lumba -lumba, rusa, kucing, katak, kelinci atau serangga, untuk menyebutkan beberapa.

Itu dapat melayani Anda: kekuatan mekanis: apa itu, aplikasi, contohGambar 5. Impala mampu melompat hingga 3 m. Sumber: Wikimedia Commons. Arturo de Frias Marques/CC BYS-S (https: // CreativeCommons.Org/lisensi/by-sa/3.0).

Latihan

Belalang membentuk sudut 55 º dengan horizontal dan mendarat di 0.80 meter kemudian. Menemukan:

a) ketinggian maksimum tercapai.

b) Jika saya melompat dengan kecepatan awal yang sama, tetapi membentuk sudut 45º, apakah akan lebih tinggi?

c) Apa yang bisa dikatakan tentang jangkauan horizontal maksimum untuk sudut ini?

Solusi untuk

Ketika data yang disediakan oleh masalah tidak mengandung kecepatan awal v_{salah satu} Perhitungannya agak lebih melelahkan, tetapi dari persamaan yang diketahui, ekspresi baru dapat disimpulkan. Mulai dari:

X_Max = v_sapi . T_penerbangan = v_{salah satu}.cos α. T_v

Saat mendarat nanti, tinggi badannya 0 lagi, lalu:

v_{salah satu} .dosa α.T_v - ½g.T_v²= 0

Sebagai T_v Ini adalah faktor umum, disederhanakan:

v_{salah satu} .dosa α - ½g.T_v= 0

Kita bisa membersihkan t_v Dari persamaan pertama:

T_v = x_Max / v_{salah satu}.cos α

Dan ganti yang kedua:

v_{salah satu} .dosa α - (½g.X_Max / v_{salah satu}.cos α) = 0

Dengan mengalikan semua istilah dengan v_{salah satu}.cos αEkspresi tidak berubah dan penyebut menghilang:

(v_{salah satu} .dosa α.) (v_{salah satu}.cos α) - ½g.X_Max = 0

v_{salah satu}² dosa α. cos α = ½g.X_Max

Sudah bisa dibersihkan v_{salah satu} atau juga ganti identitas berikut:

Sen 2α = 2 sen α. cos α → V_{salah satu}² Sen 2α = G.X_Max

Dihitung v_{salah satu}²:

v_{salah satu}² = g.X_Max / Sen 2α = (9.8 x 0.8 / sen 110) m²/S² = 8.34 m²/S²

Dan akhirnya ketinggian maksimum:

Dan_Max= v_Oy ²/2g = (8.34 x sen² 55)/(2 x 9.8) m = 0.286 m = 28.6 cm

Solusi b

Lobster berhasil mempertahankan kecepatan horizontal yang sama, tetapi ketika sudut berkurang:

Dan_Max= v_Oy ²/2g = (8.34 x sen² 45)/(2 x 9.8) m = 0.213 m = 21.3 cm

Mencapai ketinggian yang lebih kecil.

Solusi c

Lingkup horizontal maksimum adalah:

X_Max = v_{salah satu}² Sen 2a / G

Ketika sudut bervariasi, ruang lingkup horizontal juga berubah:

X_Max = 8.3. 4 Sen 90 / 9.8  m = 0.851 m = 85.1 cm

Lompatannya lebih panjang sekarang. Pembaca dapat memverifikasi bahwa itu maksimum untuk sudut 45 º kemudian:

sin 2α = sin 90 = 1.

Referensi

1. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fisika. Edisi kedua. Bukit McGraw.
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fisik. Vol. 1. Edisi ke -3. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.