Toroid atau Toro Dona

Kami menjelaskan apa itu banteng atau banteng, karakteristiknya, volume, permukaan, aplikasi dan menunjukkan beberapa contoh

Apa itu Toroid?

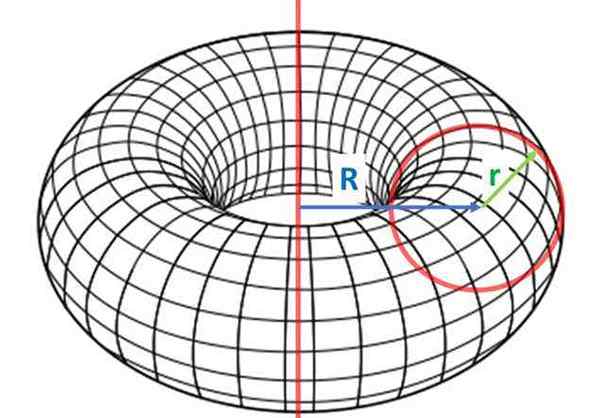
Dia Toroid Ini adalah badan geometris tiga dimensi dalam bentuk lingkaran, cincin, cincin, donat atau donat, maka nama "Toro Dona", milik kelas objek yang disebut yang disebut Revolusi Padatan.

Toroid dihasilkan dengan memutar sosok datar tertutup, di sekitar garis milik bidang yang sama dari gambar, tetapi tidak mencegatnya, seperti yang ditunjukkan di bawah ini:

Seekor banteng, yang merupakan permukaan revolusi yang diperoleh dengan memutar sosok datar tertutup (sebagai keliling) di sekitar sumbu tetap. Sumber: Wikimedia Commons

Karakteristik utama dari toroid adalah bahwa, meskipun permukaan tertutup, ia memiliki lubang. Ini berarti bahwa dua titik permukaannya dapat dihubungkan oleh segmen yang berada di luar objek.

Karakteristik lain dari toroid adalah bahwa itu adalah sosok tiga dimensi tanpa simpul. Karakteristik ini membagikannya dengan tubuh volumetrik lainnya seperti bola, tetapi sementara bola adalah permukaan cembung, banteng secara bersamaan cekung dan cembung.

Di antara lembu jantan, banteng Ini adalah yang paling umum dan diperoleh dari rotasi lingkaran radio R, Mengenai sumbu jarak R yang pertama. Radio R (dalam huruf kecil) dikenal sebagai jari -jari minor dan R (modal) adalah jari -jari terbesar.

Volume toroid

Banteng dihasilkan dengan memutar figur datar yang tertutup KE di sekitar sumbu rotasi yang tidak memotongnya. Menunjukkan oleh R Jarak dari sumbu ke centroid sosok datar, volume revolusi bull adalah:

Dapat melayani Anda: Fungsi Trigonometri Terbalik: Nilai, Derivatif, Contoh, Latihan

V = 2πr⋅ a 

Hasil ini diperoleh saat menerapkan Teorema Pappus Untuk volume padatan revolusi, yang menyatakan bahwa volume revolusi padat diperoleh dengan mengalikan area gambar yang dipecah oleh perimeter keliling yang dibentuk oleh rotasi centroid (atau pusat gravitasi ) dari gambar yang diputar, di sekitar sumbu rotasi.

Volume volume sapi jantan

Banteng adalah toroid yang dihasilkan oleh lingkaran radio R. Jika jarak sumbu rotasi ke pusat lingkaran yang diputar adalah R, maka perlu untuk volume banteng adalah:

V = (2πr) ⋅ (πr²) = 2π²R³

Permukaan banteng

Jadilah sosok datar yang sederhana KE dan kontur L. Jika gambar seperti itu diputar di sekitar sumbu yang terkandung dalam bidang yang sama dari gambar, tetapi itu tidak melintasinya, maka permukaan yang dihasilkan adalah lembu jantan:

S = 2πr⋅ l

Menjadi jarak dari sumbu ke pusat gravitasi atau centroid, dari sosok generatrix.

Hasil ini adalah konsekuensi dari Teorema Pappus Untuk permukaan revolusi yang solid.

Permukaan banteng

Bull Circular Cross -Sectional dari Radio R (huruf kecil) dan Walikota R (huruf besar) adalah banteng tertentu yang disebut Toro.

Sebagai kontur l dari lingkaran radius r 2πr, Kemudian area permukaan banteng tersebut adalah:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Aplikasi Toroid

Karena karakteristik geometrisnya, banteng memiliki aplikasi praktis dan budaya yang tak terhitung jumlahnya. Untuk memulai, lingkaran atau cincin adalah bagian toroidal yang memiliki berbagai kegunaan:

Dapat melayani Anda: kotak minimum

Kultural

• Penggunaan hias atau kosmetik saat cincin ditempatkan di jari, atau saat menusuk ditempatkan di telinga.
• Di hidung lembu, lingkaran ditempatkan, yang berfungsi untuk mengikatnya dan mengendalikannya.
• Saat cincin atau cincin ditempatkan di tangan kiri di jari manis, maka ia memiliki konotasi sosial, yang berasal dari masa orang Yunani kuno, dan menunjukkan komitmen, kesetiaan dan pernikahan dengan pasangan yang membawa lingkaran yang sama cara dan materi.

Dalam mekanika

Di luar konteks hias, kosmetik dan budaya, banteng memiliki banyak aplikasi praktis. Dalam mekanik, toroid digunakan sebagai cincin retensi bantalan di ujung sumbu kendaraan. 

Juga bantalan kendaraan bermotor dibentuk oleh satu atau dua lingkaran dalam bentuk banteng dengan berbagai bentuk penampang, di mana mereka menggulung silinder atau bola, dengan tujuan mengurangi gesekan pada sumbu.

Dalam listrik

Dalam aplikasi listrik, toroid juga sangat penting, karena inti feromagnetik induktor, elektromager dan transformator, sering memiliki bentuk banteng dan di atasnya kabel dalam bentuk kumparan.

Tokamak

Ada jenis reaktor fusi terkontrol dalam bentuk toroid atau donat yang disebut nama Rusia: tOkamak. Dalam jenis reaktor fusi nuklir ini, wadah dan kumparan yang menghasilkan medan magnet kurungan plasma memiliki bentuk atau disposisi toroidal.

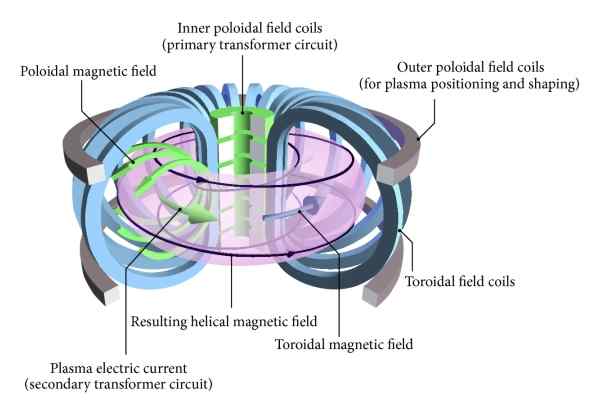Gambar secara skematis menunjukkan reaktor fusi nuklir terkontrol dalam bentuk toroidal yang dikenal sebagai "tokamak". Dalam jenis reaktor ini baik plasma, kumparan dan medan magnet kurungan memiliki konfigurasi toroidal. Sumber: Wikimedia Commons

Contoh

Permukaan banteng bagian persegi (dengan formula)

Dalam contoh ini, banteng bagian persegi dianggap seperti yang ditunjukkan pada gambar berikut:

Dapat melayani Anda: Segitiga Scaleno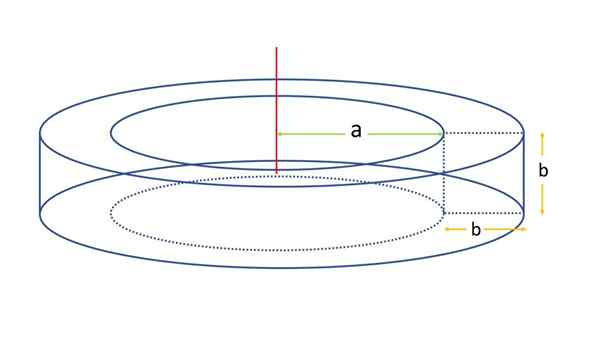 Bagian persegi Toroid. Sumber: f. Zapata

Permukaan akan ditentukan menggunakan formula permukaan untuk banteng umum. Untuk tujuan ini, perlu mengetahui jarak sumbu rotasi ke centroid kuadrat, yang, menggunakan nomenklatur sebelumnya R:

R = a + b/2

Juga perlu untuk mengetahui perimeter L dari figur generatrix, yang seperti dalam kasus ini adalah kuadrat di samping B, Konturnya akan panjang:

L = 4⋅b

Kemudian formula permukaan banteng diterapkan:

S = 2πr⋅l

Mengganti R dan L untuk ekspresi yang sesuai, tergantung pada langkah -langkah A dan B dari Square Bull adalah:

S = 2π (a + b/2) ⋅4⋅b = 8π (a + b/2) ⋅b

Permukaan toroid persegi (jumlah wajahnya)

Banteng persegi dari gambar sebelumnya terdiri dari empat wajah: bagian atas dan bawah adalah cincin datar, dan interior dan eksteriornya silinder.

Mempertimbangkan ini, dimungkinkan untuk menghitung permukaannya dengan menambahkan luas keempat wajahnya.

Wajah atas dan bawah memiliki area yang sama dengan lingkaran luar jari -jari (A+B) Kurang dari lingkaran dalam radio ke, yang merupakan hasilnya:

S_S= S_yo= π [(a+b)² - B²] = π⋅ [a²+ 2ab]

Wajah silinder internal memiliki area:

S₁= 2πab

Dan wajah silinder eksternal memiliki area:

S₂= 2π (a+b) b = 2πab+2πb²

Sehingga total luas toroid akan menjadi jumlah s_S+S_yo+S₁+S₂:

A = 2π⋅ [a²+ 2ab]+2πab+2πab+2πb².