Properti transformasi linier, apa saja penggunaan, jenis, contoh

A Transformasi linier, yang hanya akan kita sebut, menghubungkan elemen -elemen dari dua ruang vektor V dan W, menugaskan masing -masing vektor v milik v vektor tunggal W yang menjadi milik W, melalui operasi tertentu.

Transformasi ini memenuhi dua syarat:

Gambar 1. Transformasi linier berlaku untuk vektor ruang vektor V untuk mendapatkan vektor lain milik ruang vektor w. Sumber: f. Zapata.

-Kondisi 1

Ini mengacu pada penambahan, sehingga transformasi linier harus dipenuhi bahwa:

T (v + W) = T (v) + T (W)

-Kondisi 2

Kondisi kedua mewakili homogenitas dalam penggandaan skalar dengan vektor:

T (cv) = c⋅t (v)

Transformasi linier, sesuai namanya, bertanggung jawab untuk memetakan atau mengubah elemen V menjadi elemen w.

Notasi untuk fungsi juga digunakan dalam kasus transformasi linier, dengan demikian, domain V adalah himpunan elemen (vektor) yang akan diubah, sedangkan kodominium atau rute adalah set yang dihasilkan.

Contoh transformasi linier adalah:

Untuk menunjukkan bahwa huruf t akan digunakan. Transformasi akan diterapkan ke vektor v yang komponennya adalah x dan y, yang telah diwakili oleh satu kolom matriks. Hasilnya adalah vektor lain W yang komponennya adalah x dan 0, juga diwakili oleh matriks kolom.

Oleh karena itu, ini adalah transformasi ruang vektor r² Menuju ruang vektor r², Singkatnya itu ditulis seperti ini:

T: r² → R²         

Jika kita memiliki vektor:

Transformasi mengembalikan kita:

Dan dengan demikian dengan vektor r². Dalam Contoh 1 akan diverifikasi bahwa transformasi ini linier.

[TOC]

Sifat transformasi linier

Misalkan transformasi linear V di w, di mana vektor v Dan atau Mereka milik V, maka sifat -sifat berikut dipenuhi:

Properti 1

T (0) = 0

Di mana 0 adalah vektor nol.

Properti 2

T (-v) = - t (v)

Properti 3

T (atau  - v) = T (atau) - T (v)

Properti 4

Menjadi v = c₁v₁ + C₂v₂ +.. . +  C_Nv_N

 Jadi:

T (c₁v₁ + C₂v₂ +.. . +  C_Nv_N) = c₁ T (v₁) + c₂ T (v₂) +.. . +  C_N T (v_N)

Elemen transformasi linier

Biarkan V dan W telah menyebutkan ruang vektor di mana transformasi linier T mengubah elemen v ke w. Kita dapat mendefinisikan elemen -elemen berikut:

-C nukleus atau kernel: Itu adalah subset dari domain yang dilambangkan olehnya N (t) salah satu ker (t) dan pahami semua elemen V sedemikian rupa sehingga:

T (v) = 0.

Transformasi linier t (v) = 0 disebut transformasi nol.

Secara alami vektor nol v = 0 tetap memenuhi kondisi ini, tetapi kernel terdiri dari seluruh vektor non -non -non -non -non -non -non.

Dapat melayani Anda: Fungsi Tumbuh: Cara Mengidentifikasi, Contoh, Latihan

-Gambar t: Itu adalah himpunan vektor milik w sedemikian rupa sehingga merupakan gambar dari setidaknya beberapa vektor di v. Itu dilambangkan sebagai Im t) Dan itu adalah bagian dari ruang vektor w.

Elemen -elemen ini akan membantu kita mengklasifikasikan transformasi linier nanti.

Untuk apa transformasi linier?

Awalnya, transformasi linier bekerja dengan ruang vektor, dibentuk oleh vektor. Berkali -kali kami mengasosiasikan vektor dengan kekuatan dan besaran fisik lainnya, namun dalam pemrosesan gambar digital, piksel dapat diwakili oleh vektor.

Dalam hal ini, gambar dapat dimanipulasi dengan transformasi linier yang nyaman untuk mendapatkan efek yang diinginkan, misalnya memproyeksikan, berputar, menemukan gambar cermin atau memodifikasi ukurannya tanpa mengubah dimensi relatif.

Transformasi linier juga banyak digunakan dalam bidang ekonomi dan pengambilan keputusan, misalnya untuk mengetahui jumlah bahan baku yang dibutuhkan untuk memproduksi batch produk tertentu.

Jumlah bagian yang diperlukan untuk merakit berbagai model yang diproduksi oleh pabrik, dapat dikerjakan melalui pengaturan matriks, seperti yang akan kita lihat nanti.

Jenis Transformasi Linier (Klasifikasi)

Seperti fungsi, transformasi linier bisa:

-Suntikan atau Monomorfisme

-BYJECTIVES atau Epimorfisme

-Overjective atau Isomorfisme

Selain itu adalah tipe berikut:

-Endomorfisme

-Automorfisme.

Transformasi linear injeksi

Biarkan ruang vektor v dan w dan t transformasi linier t: v → w. T suntikan saat:

Ker (T) = 0

Transformasi overjective linear

Jika V dan W adalah ruang vektor sedemikian rupa sehingga t: v → w, dikatakan bahwa t adalah buta jika:

Im (t) = w

Transformasi linier yang Bijjective

Transformasi linier T: V → W bersifat buta saat itu adalah suntikan dan overjective. Oleh karena itu terpenuhi bahwa:

Ker (T) = 0 Dan Im (t) = w

Endomorfisme

Mereka adalah transformasi linier di mana domain dan kodominium bertepatan.

Automorfisme

Jenis transformasi linier ini adalah endomorfisme bypective.

Transformasi Linear Khusus

Operator linier

Transformasi linier T: V → V, yang beralih dari ruang vektor ke ruang vektor yang sama disebut Operator linier.

Nol transformasi

Disebutkan di atas, transformasi nol penting untuk menemukan kernel transformasi linier:

Itu bisa melayani Anda: tetradecágon

T: v → w sehingga t (v) = 0 Untuk apapun v.

Transformasi identitas

T: v → v sedemikian rupa sehingga t (v) = v  Untuk apapun v.

Transformasi yang ditentukan oleh matriks

T: v → w sehingga t (v) = Av, dimana a adalah matriks dan v Itu adalah vektor kolom.

Funtion Lineal

Fungsi linier tipe y = mx adalah transformasi linier. Ambil contoh y = 3x dan lihat apakah memenuhi dua kondisi awal, pengujian dengan dua nilai a dan b any:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Memang itu adalah transformasi linier.

Aplikasi

Transformasi linier memiliki aplikasi matematika, seperti:

-Koordinat rotasi as.

-Dalam solusi sistem persamaan diferensial linier.

-Masalah Nilai Diri dan Autovery.

Dan mereka juga memiliki aplikasi di bidang sains lainnya, misalnya dalam mekanika, mekanika kuantum dan ekonomi, di antara bidang lainnya.

Contoh transformasi linier

Contoh 1

Dalam banyak masalah mekanik kita perlu menemukan proyeksi vektor v milik ruang, di pesawat tertentu. Vektor ini v dapat mewakili misalnya kekuatan.

Misalkan Anda ingin memproyeksikan vektor v = Di bidang xy. Kita dapat mendefinisikan transformasi linier yang diberikan oleh matriks berikut:

Saat kami menerapkannya pada vektor v Kami mendapatkan vektor yang komponen Z yang dibatalkan. Secara geometris diwakili, dengan proyeksi v Pada bidang XY sebagai vektor merah dengan dua komponen.

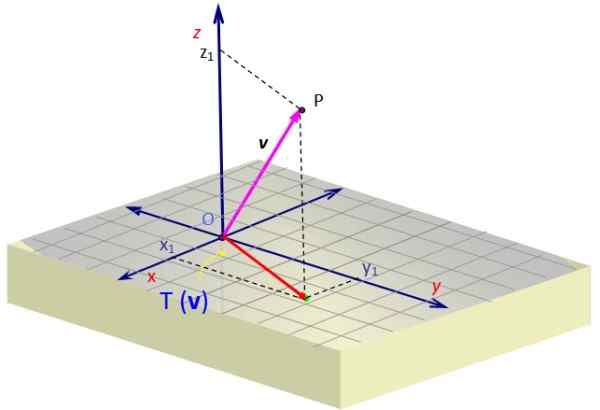Gambar 2. Proyeksi vektor dalam ruang pada pesawat, yang diperoleh melalui transformasi linier. Sumber: f. Zapata.

Contoh 2

Misalkan Anda memiliki pabrik yang menghasilkan tiga jenis gerobak mainan: C1, C2 dan C3, yang pada gilirannya Anda membutuhkan tiga jenis bagian dalam jumlah tertentu untuk memproduksi setiap jenis gerobak:

-Kapak atau bagian

-Roda atau potongan b

-Sasis atau bagian c

Untuk setiap jenis keranjang, jumlah potongannya berbeda, karena modelnya berbeda. Kami dapat mengakomodasi jumlah dalam matriks 3 × 3, di mana kolom dipimpin oleh jenis gerobak, dan peringkatnya sesuai dengan jumlah potongan yang diperlukan untuk menguraikan setiap model.

Ini adalah contoh transformasi yang diberikan oleh matriks yang akan seperti ini:

Jika pabrik menerima pesanan pembelian tertentu, yang terdiri dari X Jumlah C1, Dan  dari C2 dan z Dari C3, berapa banyak bagian A, B dan C yang perlu tersedia untuk merakit gerobak pesanan?

Itu dapat melayani Anda: apa itu ekspresi aljabar dan mana yang paling sering?

Kita harus menemukan transformasi linier t (x) sehingga:

Untuk mendapatkan vektor dan:

Yang akan memberi kita jumlah bagian yang harus kita miliki. Pada tahun ini diselesaikan 2 kami mengevaluasi efektivitas transformasi linier untuk menemukan jumlah bagian yang diperlukan untuk memenuhi pesanan tertentu.

Latihan terpecahkan

- Latihan 1

Periksa apakah transformasi berikut t: r² → R² Itu linier:

Larutan

Untuk melakukan ini, Anda harus memastikan bahwa transformasi memenuhi dua kondisi yang dijelaskan di awal, pertama penambahan dan kemudian produk skalar untuk vektor. Jadi Anda harus mengambil dua vektor v Dan  atau milik r², menulisnya dengan notasi matriks atau menentukan komponen.

Vektor -vektor ini adalah:

v = x₁, Dan₁

atau = x₂, Dan₂

Kondisi pertama

-Mengingat bahwa vektor ditambahkan komponen komponen, harus diverifikasi bahwa:

T (v+atau) = T (v) + T (atau)

T (v+atau) = T (x₁+ X₂ ; Dan₁ + Dan₂)

Dari sini diperoleh itu:

T (x₁+ X₂ ; Dan₁ + Dan₂) = (x₁+ X₂; 0)

-Di sisi lain, saat menerapkan transformasi ke setiap vektor secara terpisah:

T (x₁,Dan₁) + T (x₂,Dan₂) = (x₁,0) + (x₂,0)

Dengan menambahkan vektor yang dihasilkan, ia diperoleh secara efektif:

W = (X₁+ X₂; 0)

Karena kedua hasilnya identik, kondisi pertama dipenuhi.

Kondisi kedua

Sekarang kita akan memverifikasi bahwa dengan mengalikan dengan Scler C, itu bisa keluar dari transformasi:

T (cv) = c⋅t (v)

Sean:

v = x₁, Dan₁

C.v = C⋅x₁, C⋅y₁

Jadi:

T (cv) = T (c⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Tapi kita tahu itu dari langkah sebelumnya bahwa t (v) = T (x₁, Dan₁ ) = (X₁ , 0).

Jadi karena kedua ekspresi identik, kondisi kedua juga terpenuhi dan transformasi linier.

- Latihan 2

Sebuah pabrik gerobak mainan merakit tiga model kendaraan: C1, C2 dan C3, yang Anda butuhkan potongan A, B dan C yang masing -masing pakan, roda dan sasis. Jumlah yang diperlukan ada di tabel berikut:

Pabrik telah diminta untuk menyiapkan 12 model C1, 22 C2 dan 16 C3. Berapa banyak bagian A, B dan C yang diperlukan untuk menyelesaikan pesanan?

Larutan

Transformasi linier t (x) = y diterapkan, yang hasilnya adalah produk antara matriks:

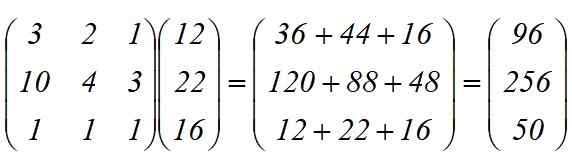
Mereka dibutuhkan secara total:

-96 sumbu

-256 roda

-50 sasis.

Referensi

1. Aljabar dan geometri analitik. Inti dan gambar. Klasifikasi transformasi linier. Dipulihkan dari: AGA.FRBA.Utn.Edu.ar.
2. Grossman, s. 2012. Aljabar linier. 7. Edisi. Bukit McGraw.
3. Gutiérrez, e. 2014. Aljabar linier dan aplikasinya. Grup Editorial Patria.
4. Larson, r. 2016. Dasar -dasar aljabar linier. 6. Edisi. Pembelajaran Cengage.
5. Wikipedia. Aplikasi linier. Pulih dari: is.Wikipedia.org.