Halaman rumah
Matematika
Sifat trapeze persegi panjang, hubungan dan formula, contoh

Matematika

Sifat trapeze persegi panjang, hubungan dan formula, contoh

4235
594
Joseph Nader PhD

A Trapeze persegi panjang Itu adalah sosok datar dari empat sisi, sehingga dua dari mereka sejajar satu sama lain, disebut pangkalan Dan juga salah satu sisi lain tegak lurus terhadap pangkalan.

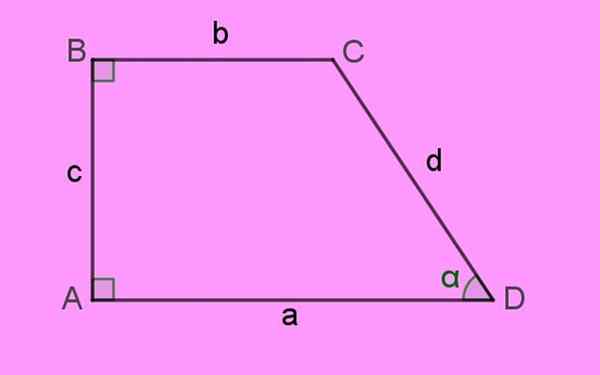
Untuk alasan ini, dua sudut internal lurus, yaitu, mereka mengukur 90º. Oleh karena itu nama "persegi panjang" yang diberikan kepada gambar tersebut. Gambar trapeze persegi panjang berikut mengklarifikasi karakteristik ini:

[TOC]

Elemen trapeze

Elemen trapesium adalah:

-Pangkalan

-Sudut

-Tinggi

-Sudut internal

-Basis rata -rata

-Diagonal

Kami akan merinci elemen -elemen ini dengan bantuan Gambar 1 dan 2:

Gambar 1. Trapeze persegi panjang, ditandai dengan memiliki dua sudut internal 90º: A dan B. Sumber: f. Zapata.

Sisi trapesium persegi panjang dilambangkan dengan huruf kecil A, B, C dan D. Sudut sosok atau Sudut Mereka ditunjukkan dalam huruf kapital. Akhirnya Sudut internal Mereka diekspresikan dengan surat -surat Yunani.

Menurut definisi tersebut, pangkalan Dari trapesium ini adalah sisi A dan B, yang seperti yang diamati paralel dan juga memiliki panjang yang berbeda.

Sisi tegak lurus ke kedua pangkalan adalah sisi C di sebelah kiri, yang merupakan tinggi H dari trapeze. Dan akhirnya ada sisi D, yang membentuk sudut akut α dengan sisi a.

Jumlah dari Sudut internal dari segi empat adalah 360º. Mudah dihargai bahwa sudut yang hilang C pada gambar adalah 180 - α.

Itu basis rata -rata Ini adalah segmen yang bergabung dengan sisi tengah sisi non -paralel (segmen EF pada Gambar 2).

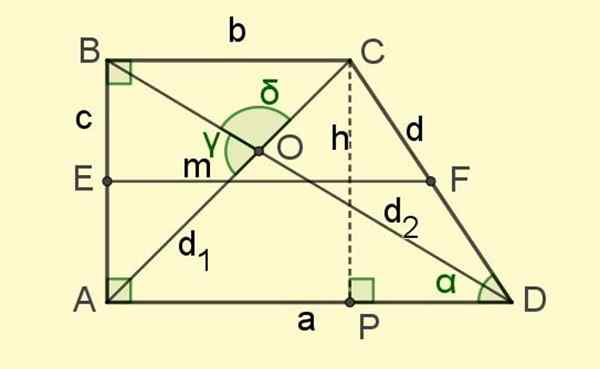Gambar 2. Elemen trapesium persegi panjang. Sumber: f. Zapata.

Dan akhirnya ada diagonal D₁ dan d₂, Segmen yang menyatukan simpul yang berlawanan dan yang berpotongan pada titik O (lihat Gambar 2).

Hubungan dan formula

Tinggi h dari trapesium

H = c

Perimeter p

Ini adalah ukuran kontur dan dihitung dengan menambahkan sisi:

Perimeter = A + B + C + D

Sisi D Itu dinyatakan dalam hal tinggi atau sisi C Melalui Teorema Pythagoras:

D = √ (A-B)² + C²

Mengganti di perimeter:

P = A + B + C + √ (A-B)² + C²

Basis rata -rata

Itu adalah semi -bodi pangkalan:

Basis sedang = (a+b)/2

Terkadang basis rata -rata yang diekspresikan dengan cara ini ditemukan:

Basis sedang = (basis utama + basis minor) /2

Daerah

Area A dari trapeze adalah produk dari basis rata -rata berdasarkan tinggi:

A = (Basis utama + basis minor) x Tinggi /2

A = (a+b) c/2

Diagonal, sisi dan sudut

Beberapa segitiga muncul pada Gambar 2, baik persegi panjang maupun non -rektik. Bagi mereka yang benar -benar segitiga, mereka dapat diterapkan oleh teorema Pythagoras dan mereka yang tidak, teorema kosinus dan payudara.

Dapat melayani Anda: Angka transenden: Apa itu, formula, contoh, latihan

Dengan cara ini ada hubungan antara sisi dan antara sisi dan sudut internal trapezio.

Segitiga CPA

Itu adalah persegi panjang, kakinya sama dan layak B, sedangkan hipotenus adalah diagonal D₁, Karena itu:

D₁² = b² + B² = 2b²

Dab Triangle

Itu juga persegi panjang, kakinya ke Dan C (atau juga ke Dan H) Dan hipotenus adalah D₂, sehingga:

D₂² = a² + C²= a² + H²

Segitiga CDA

Karena segitiga ini bukan persegi panjang, teorema kosinus diterapkan, atau juga payudara.

Menurut Teorema Coseno:

D₁² = a² + D² - 2AD cos α

Segitiga CDP

Segitiga ini adalah persegi panjang dan dengan sisi -sisinya, alasan trigonometri sudut α dibangun:

sin α = h/d

cos α = pd/d

Tetapi sisi Pd = A - B, oleh karena itu:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Anda juga memiliki:

TG α = sin α / cos α = H / (A-B) → H = TG α (A-B)

Segitiga CDB

Dalam segitiga ini kita memiliki sudut yang simpulnya di C. Itu tidak ditandai dalam gambar, tetapi pada awalnya menonjol bahwa itu bernilai 180 - α. Segitiga ini bukan persegi panjang, jadi teorema cosinus atau teorema payudara dapat diterapkan.

Sekarang, dapat dengan mudah ditunjukkan bahwa:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Menerapkan Teorema Coseno:

D₂² = d² + B²- 2dB cos (180 - α) = D² + B²+ 2dB cos α

Contoh persegi panjang

Trapezios dan khususnya persegi panjang ditemukan di banyak sisi, dan terkadang tidak selalu nyata. Di sini kami memiliki beberapa contoh:

Trapecio sebagai elemen desain

Angka geometris berlimpah dalam arsitektur berbagai bangunan, seperti gereja ini di New York, yang menunjukkan struktur dalam bentuk trapesium persegi panjang.

Juga bentuk trapesium sering dalam desain wadah, wadah, bilah (Pemotong atau tepat), lembaran dan dalam desain grafis.

Gambar 3. Malaikat di dalam trapesium persegi panjang di sebuah gereja di New York. Sumber: David Goehring melalui Flickr.

Generator Gelombang Trapesium

Sinyal listrik tidak hanya bisa persegi, sinus atau segitiga. Ada juga sinyal trapesium yang berguna di berbagai sirkuit. Pada Gambar 4 ada sinyal trapesium yang terdiri dari dua persegi panjang. Di antara mereka mereka membentuk satu trapesium Isosceles tunggal.

Dapat melayani Anda: pembagi 8: apa itu dan penjelasan yang mudah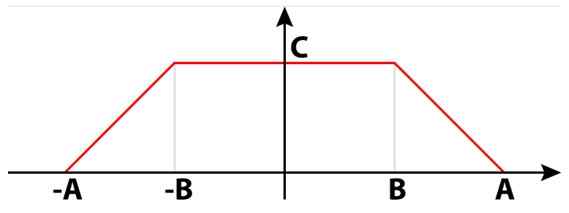

Gambar 4. Sinyal trapesium. Sumber: Wikimedia Commons.

Dalam perhitungan numerik

Untuk menghitung secara numerik integral yang ditentukan dari fungsi f (x) antara A dan B, aturan trapeze digunakan untuk memperkirakan area di bawah grafik f (x). Pada gambar berikut, di sebelah kiri pendekatan integral dengan trapesium persegi panjang tunggal.

Pendekatan yang lebih baik adalah sosok yang tepat, dengan beberapa persegi panjang.

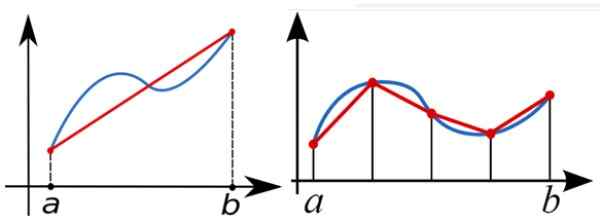Gambar 5. A yang didefinisikan integral antara A dan B tidak lain adalah area di bawah kurva f (x) antara nilai -nilai ini. Trapesium persegi panjang dapat berfungsi sebagai pendekatan pertama untuk area itu, tetapi semakin banyak trapesium digunakan, semakin baik pendekatannya. Sumber: Wikimedia Commons.

Balok beban trapesium

Kekuatan tidak selalu terkonsentrasi pada satu titik, karena tubuh tempat mereka bertindak memiliki dimensi yang cukup besar. Begitulah kasus jembatan di mana kendaraan terus beredar, air kolam di dinding vertikal yang sama atau atap di mana air atau salju menumpuk.

Itulah sebabnya kekuatan didistribusikan per unit panjang, permukaan atau volume, tergantung pada tubuh yang mereka lakukan.

Dalam kasus balok, gaya yang didistribusikan per unit panjang dapat memiliki berbagai distribusi, misalnya bahwa trapeze persegi panjang yang ditunjukkan di bawah ini:

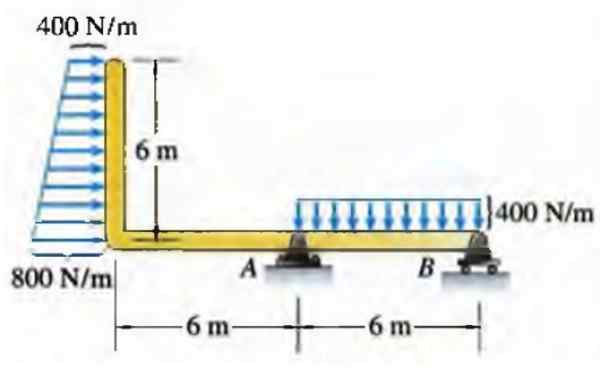Gambar 6. Memuat di balok. Sumber: Bedford, TO. seribu sembilan ratus sembilan puluh enam. Statis. Addison Wesley Inter -American.

Pada kenyataannya, tidak selalu distribusi sesuai dengan bentuk geometris reguler seperti ini, tetapi mereka bisa menjadi pendekatan yang baik dalam banyak kasus.

Sebagai alat pendidikan dan pembelajaran

Blok dan lembar dengan bentuk geometris, termasuk trapesium, sangat berguna bagi anak -anak untuk membiasakan diri sejak usia dini dengan dunia geometri yang menarik.

Gambar 7. Blok dengan bentuk geometris sederhana. Berapa banyak persegi panjang yang tersembunyi di blok? Sumber: Wikimedia Commons.

Latihan terpecahkan

- Latihan 1

Dalam trapesium persegi panjang pada Gambar 1, basis terbesar bernilai 50 cm dan basis terkecil sama dengan 30 cm, juga diketahui bahwa sisi miring berukuran 35 cm. Menemukan:

a) sudut α

b) tinggi

c) Perimeter

D) dasar sedang

e) area

f) Diagonal

Solusi untuk

Data pernyataan dirangkum dengan cara ini:

A = basis yang lebih tinggi = 50 cm

B = basis minor = 30 cm

D = sisi miring = 35 cm

Dapat melayani Anda: Operasi Dasar

Untuk menemukan sudut α, kami mengunjungi bagian Formula dan Persamaan, untuk melihat mana yang paling sesuai dengan data yang ditawarkan. Sudut yang dicari ditemukan di beberapa segitiga yang dianalisis, misalnya CDP.

Di sana kami memiliki formula ini, yang berisi yang tidak diketahui dan juga data yang kami tahu:

cos α = (a-b) / d

Karena itu:

α = lengkungan [(a-b) / d] = lengkungan [(50-30) / 35] = lengkungan 20/35 = 55.15 º

Solusi b

Dari persamaan:

sin α = h/d

h = d.dosa α = 35 sen 55.15 º cm = 28.72 cm

Solusi c

Perimeter adalah jumlah sisi, dan karena tingginya sama dengan sisi C, kita harus:

C = H = 28.72 cm

Karena itu:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Solusi d

Basis rata -rata adalah semi -bodi pangkalan:

Basis sedang = (50 + 30 cm)/2 = 40 cm

Solusi e

Area trapesium adalah:

A = Basis rata -rata x tinggi = 40 cm x 28.72 = 1148.8 cm².

Solusi f

Untuk diagonal D₁ Formula ini dapat digunakan:

D₁² = b² + B² = 2b²

D₁²= 2 x (30 cm)² = 1800 cm²

D₁ = √1800 cm² = 42.42 cm

Dan untuk diagonal D₂:

D₂² = d² + B²+ 2dB cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 º = 3325 cm²

D₂ = √ 3325 cm² = 57.66 cm

Ini bukan satu -satunya cara untuk menemukan D₂, Karena ada juga segitiga Dab.

- Latihan 2

Grafik kecepatan berikut tergantung pada ponsel yang memiliki gerakan lubur yang dipercepat secara seragam. Hitung jarak yang ditempuh oleh ponsel selama interval waktu antara 0.5 dan 1.2 detik.

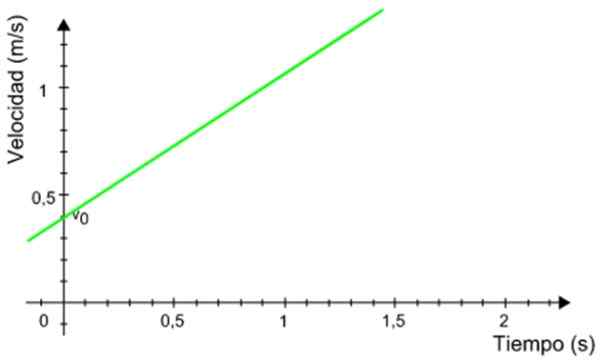Angka 8. Grafik terhadap waktu ponsel dengan gerakan reknet yang dipercepat secara seragam. Sumber: Wikimedia Commons.

Larutan

Jarak yang ditempuh oleh ponsel setara dengan area di bawah grafik, dibatasi oleh interval waktu yang ditunjukkan.

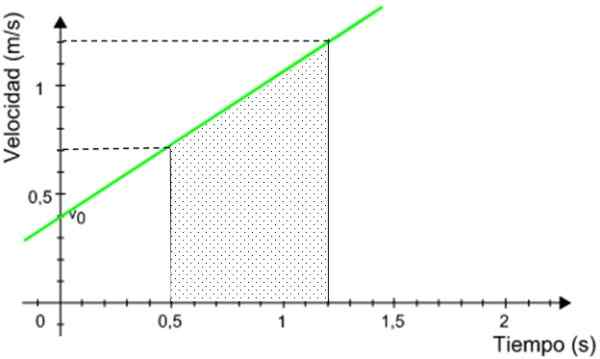Gambar 9. Jarak yang ditempuh oleh ponsel setara dengan area di bawah grafik. Sumber: dimodifikasi oleh f. Zapata.

Area teduh adalah area trapesium persegi panjang, diberikan oleh: