Acutangle Triangle

Apa segitiga acutangulus?

Itu Segitiga Acutangulus Mereka adalah mereka yang tiga sudut internal adalah sudut akut; yaitu, ukuran masing -masing sudut tersebut kurang dari 90 ° derajat. Dengan tidak memiliki sudut yang tepat, kami memiliki teorema Pythagoras tidak terpenuhi untuk sosok geometris ini.

Oleh karena itu, jika kita ingin memiliki beberapa jenis informasi tentang sisi atau sudutnya, perlu menggunakan teorema lain yang memungkinkan kita memiliki akses ke data ini. Yang dapat kita gunakan adalah teorema payudara dan teorema kosinus.

Karakteristik segitiga acutangle

Di antara karakteristik yang dimiliki sosok geometris ini, kita dapat menyoroti yang diberikan oleh fakta sederhana menjadi segitiga. Di antara ini kita harus:

- Segitiga adalah poligon yang memiliki tiga sisi dan tiga sudut.

- Jumlah dari tiga sudut internalnya sama dengan 180 °.

- Jumlah dua sisinya selalu lebih besar dari yang ketiga.

Sebagai contoh, mari kita lihat segitiga ABC berikut. Secara umum, kami mengidentifikasi sisi mereka dengan huruf kecil dan sudutnya dengan huruf kapital, sehingga sisi dan sudut yang berlawanan memiliki huruf yang sama.

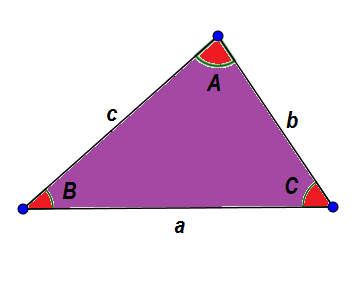
Karena karakteristik yang sudah diberikan, kita tahu itu:

A + B + C = 180 °

A + B> C, A + C> B dan B + C> A

Karakteristik utama yang membedakan jenis segitiga ini dari yang lain adalah, seperti yang telah kita sebutkan, sudut internalnya akut; yaitu, ukuran masing -masing sudutnya kurang dari 90 °.

Segitiga acutangulus, bersama dengan segitiga tumpul (yang di mana salah satu sudutnya memiliki ukuran lebih besar dari 90 °), adalah bagian dari set segitiga miring. Set ini dibentuk oleh segitiga yang bukan persegi panjang.

Dapat melayani Anda: apa elemen perumpamaan? (Bagian)

Dengan menjadi bagian dari segitiga miring, kita harus memecahkan masalah di mana Acutangulus Triangles campur tangan harus menggunakan teorema payudara dan teorema kosinus.

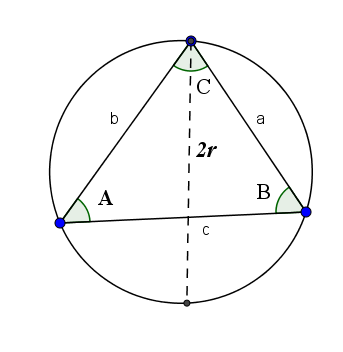
Teorema payudara

Teorema payudara menegaskan bahwa alasan di satu sisi dengan dada sudut yang berlawanan sama dengan dua kali jari -jari lingkaran yang dibentuk oleh tiga simpul segitiga tersebut. Artinya:

2r = a/sin (a) = b/sen (b) = c/sen (c)

Teorema Coseno

Di sisi lain, teorema Coseno memberi kita tiga persamaan ini untuk setiap segitiga ABC:

ke²= b² + C² -2bc*cos (a)

B²= a² + C² -2ac*cos (b)

C²= a² + B² -2ab*cos (c)

Teorema ini juga dikenal sebagai hukum sinus dan hukum kosinus, masing -masing.

Fitur lain yang dapat kita berikan dari segitiga acutangulous adalah bahwa dua di antaranya sama jika mereka memenuhi salah satu kriteria berikut:

• Jika mereka memiliki ketiganya.
• Jika mereka memiliki sisi dan dua sudut sama satu sama lain.
• Jika mereka memiliki dua sisi dan sudut yang sama.

Jenis Segitiga Acutángulos

Segitiga acutangulus dapat diklasifikasikan menurut sisi mereka. Ini mungkin:

Acutangulos sisi segitiga

Mereka adalah segitiga acutangulous yang memiliki semua sisi yang sama dan, oleh karena itu, semua sudut internal mereka memiliki nilai yang sama, yaitu A = B = C = 60 ° derajat.

Sebagai contoh, mari kita ambil segitiga berikut, yang sisi -sisi A, B dan C memiliki nilai 4.

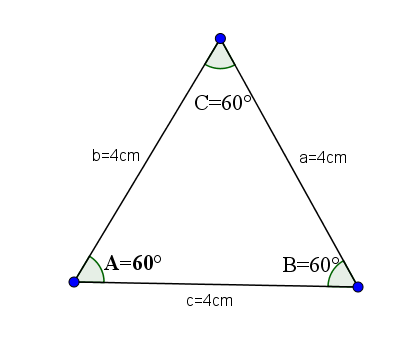
Segitiga Acutángulos Isosceles

Segitiga ini, selain memiliki sudut internal akut, memiliki karakteristik memiliki dua sisi yang sama dan yang ketiga, yang umumnya dianggap sebagai dasar, berbeda.

Contoh dari jenis segitiga ini bisa menjadi orang yang alasnya 3 dan dua sisi lainnya memiliki nilai 5. Dengan langkah -langkah ini akan memiliki sudut yang bertentangan dengan sisi yang sama dengan nilai 72,55 ° dan sudut yang berlawanan dari pangkalan adalah 34,9 °.

Dapat melayani Anda: sudut nol: definisi dan karakteristik, contoh, latihan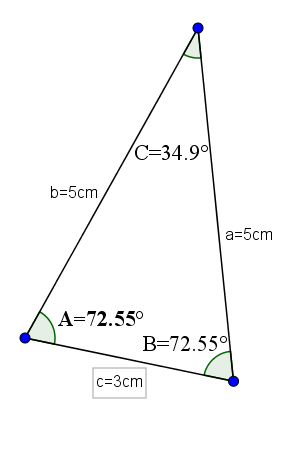

Segitiga scalene acutangulus

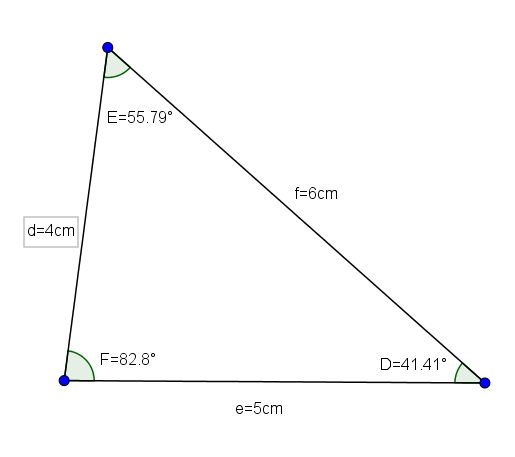
Ini adalah segitiga yang memiliki semua sisi berbeda dua hingga dua. Oleh karena itu, semua sudutnya, selain kurang dari 90 °, berbeda dua hingga dua.

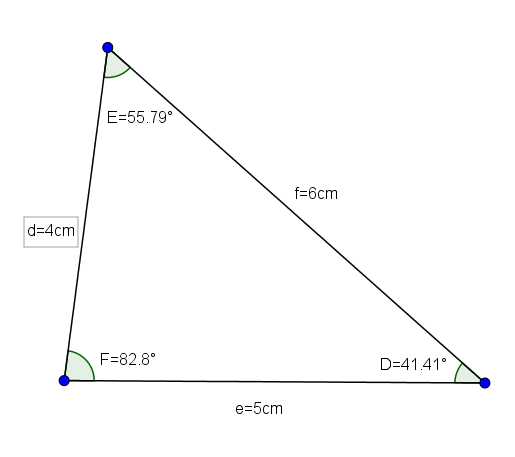
Def segitiga (yang ukurannya adalah d = 4, e = 5 dan f = 6 dan sudutnya adalah d = 41.41 °, E = 55.79 ° dan f = 82.8 °) adalah contoh yang baik dari scalene segitiga akutangle acutangle.

Resolusi segitiga acutangles

Seperti yang kami katakan sebelumnya, untuk penyelesaian masalah di mana segitiga acutangulus campur tangan.

Contoh 1

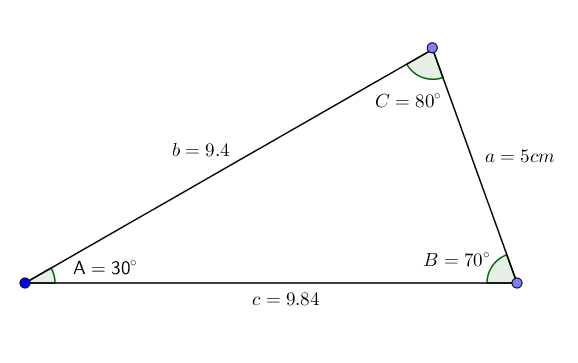
Diberi segitiga ABC dengan sudut A = 30 °, B = 70 ° dan sisi A = 5cm, kami ingin mengetahui nilai sudut C dan sisi B dan C.

Hal pertama yang kami lakukan adalah menggunakan fakta bahwa jumlah sudut internal segitiga adalah 180 °, untuk mendapatkan nilai sudut C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Kami membersihkan C dan kami memiliki:

C = 180 ° - 100 ° = 80 °

Seperti yang kita ketahui tiga sudut dan satu sisi, kita dapat menggunakan teorema payudara untuk menentukan nilai sisi yang tersisa. Untuk teorema kita harus:

a/sin (a) = b/sen (b) dan a/sen (a) = c/(sin (c)

Kami menghapus persamaan dan kami harus:

B = (a*sin (b))/sin (a) ≈ (5*0.940) / (0.5) ≈ 9.4

Sekarang kita hanya perlu menghitung nilai c. Kami melanjutkan analog seperti dalam kasus sebelumnya:

C = (a*sin (c))/sin (a) ≈ (5*0.984)/(0.5) ≈ 9.84

Jadi kita mendapatkan semua data segitiga. Seperti yang bisa kita perhatikan, segitiga ini memasuki kategori Segitiga Pemindaian.

Contoh 2

Diberi segitiga pertahanan dengan sisi D = 4cm, E = 5cm dan F = 6cm, kami ingin mengetahui nilai sudut segitiga tersebut.

Untuk kasus ini kita akan menggunakan hukum kosinus, yang memberitahu kita bahwa:

Dapat melayani Anda: jumlah kotak dari dua angka berturut -turut

D²= e² + F² - 2EFCOS (D)

Dari persamaan ini kita dapat menghapus cos (d), yang menghasilkan:

Cos (d) = ((4)² - (5)² -(6)²)/(-2*5*6) = 0.75

Dari sini kita harus berlabuh 41.41 °

Menggunakan Teorema Senom Sekarang kami memiliki persamaan berikut:

D/(sin (d) = e/(sin (e)

Membersihkan sen (e), kita harus:

sin (e) = e*sen (d)/d = (5*0.66)/4 ≈ 0.827

Dari sini kita harus melakukannya.79 °

Akhirnya, menggunakan jumlah sudut internal segitiga adalah 180 °, kita harus.8 °.