A genjang Itu adalah sosok datar empat sisi, -sebuah quadrilateral -di yang sisi dan sudut internalnya berbeda dua hingga dua. Oleh karena itu rhomboid milik kelompok jajaran genjang miring.

Angka geometris adalah bagian dari alam dan khususnya dari empat sisi seperti rhomboid, memiliki banyak aplikasi dalam arsitektur dan desain.

Gambar 1. Panel pencahayaan Stadion Allianz Arena di Munich, Jerman, diterangi dengan warna tim lokal dan dengan cahaya putih ketika pemilihan negara itu bermain. Sumber: Pxhere.

Up kami memiliki bagian dari fasad Stadion Sepak Bola Allianz Arena di Munich. Mereka adalah panel rhomboid yang menyala dengan warna tim lokal.

Oleh karena itu adalah sosok dengan banyak dinamisme visual, karena tidak seperti segi empat lainnya, ia tidak memiliki sumbu simetri. Gambar berikut menunjukkan berbagai rhomboid dengan bervariasi orientasi di pesawat.

Gambar 2. Beberapa rhomboid dengan orientasi berbeda di pesawat. Sumber: f. Zapata.

[TOC]

Karakteristik Romboid

Selanjutnya, karakteristik utama dari sosok geometris yang menarik ini:

-Nomor Lembar: 4.

-Jumlah simpul: 4.

-Sisi yang berlawanan adalah sama dan paralelnya, namun sisi yang berdekatan tidak setara.

-Ini memiliki 4 sudut internal: dua akut (kurang dari 90º), dilambangkan dengan huruf Yunani α dan dua tumpul (lebih dari 180º), disebut β (lihat Gambar 3).

-Dengan menambahkan dua sudut yang berdekatan dari rhomboid, 180º diperoleh, oleh karena itu α dan β adalah Tambahan.

-Jumlah 4 sudut internal sama dengan 360º.

-Diagonal adalah segmen yang dimulai dari simpul dan berakhir pada titik berlawanan.

-Titik di mana diagonal dari rhomboid intersect disebut BaryCenter.

-Diagonal rhomboid memiliki ukuran yang berbeda.

Tentang Diagonal Rhomboid Ada beberapa detail penting yang akan kita bahas di bawah.

Dapat melayani Anda: menunggu garis: formula dan persamaan, representasi, contoh

Diagonal rhomboid

Sangat penting untuk menekankan bahwa diagonal rhomboid bukan bisektrik, yaitu, mereka tidak membagi sudut internal gambar menjadi dua bagian yang sama.

Diagonal tidak tegak lurus satu sama lain. Namun, kami dapat dengan mudah menghitungnya dengan teorema kosinus. Dengan demikian, diagonal utama D_M Dalam rhomboid Gambar 3 adalah:

D_M = √ (a² + B² - 2.AB.cos β)

Dan diagonal minor D_M Saya akan:

D_M = √ (a² + B² - 2.AB.cos α)

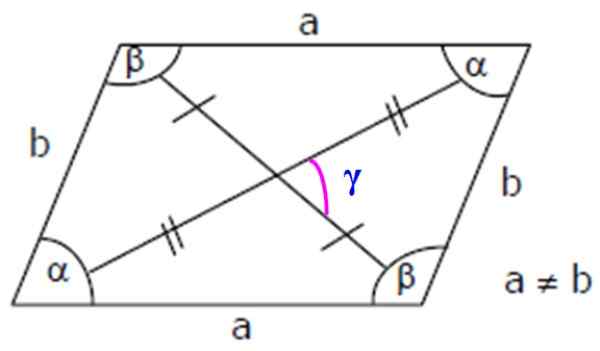Gambar 3. Elemen Romboid: Sisi, sudut internal dan diagonal. Sumber: Wikimedia Commons.

Penting: Karena α dan β adalah pelengkap, dipenuhi bahwa:

sin α = sin β

cos α = -cos β

Sifat -sifat alasan trigonometri ini harus diperhitungkan saat menyelesaikan latihan.

Cara menghilangkan perimeter dan area

Untuk menemukan perimeter dan area yang akan kami beri nama pada sisi rhomboid, ini akan ke Dan B. Kami juga memiliki ketinggian rhomboid, disebut H, yang merupakan garis yang diambil dari salah satu simpul dan diarahkan secara tegak lurus ke sisi yang berlawanan dari gambar.

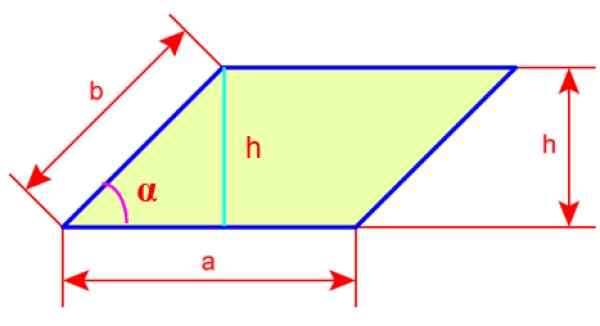Gambar 4. Sisi dan tinggi rhomboid. Sumber: Wikimedia Commons.

Perimeter rhomboid

Perimeter rhomboid dihitung dengan menambahkan panjang keempat sisinya. Mari kita panggil P ke perimeter, lalu:

P = 2a + 2b

Kami juga dapat mengekspresikannya melalui:

P = 2 (a+b)

Perimeter mengetahui ketinggiannya

Jika kita terlihat baik, tinggi H dapat ditentukan dari segitiga di sebelah kiri pada Gambar 4. Sisi B akan menjadi hipotenus dan ketinggian C cateto yang bertentangan dengan sudut α, oleh karena itu: oleh karena itu:

sin α = lawan / hypotenusa cateto

O Nah:

sin α = h / b

Lalu kami membersihkan b:

b = h / sin α

Kami mengganti di perimeter P:

P = 2 [a + (h / sin α)]

Area Romboid

Area rhomboid adalah ukuran permukaannya. Dan karena ini adalah jajaran genjang, area A -nya diberikan oleh ekspresi yang diketahui dengan baik:

Dapat melayani Anda: faktor umum untuk istilah pengelompokan: contoh, latihan

A = Dasar X Tinggi

Bahwa menurut Gambar 3 dan 4 diekspresikan melalui:

A = a x h

Area mengetahui kedua sisi dan sudut internal

Menerapkan trigonometri dasar dari bagian sebelumnya, kami menemukan ekspresi yang setara untuk area rhomboid:

h = b. dosa α

Maka area tersebut seperti ini:

A = a. B. dosa α

Mengingat apa yang kami katakan di atas tentang sudut pelengkap, kami dapat mengganti sen α dengan sen β jika perlu.

Area mengetahui diagonal dan sudut di antara mereka

Akhirnya, jika kita tahu diagonal d_M dan d_M, Ditambah sudut γ di antara mereka (lihat Gambar 3), area tersebut dapat dihitung dengan semi -produk diagonal melalui dada sudut tersebut:

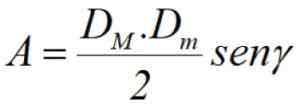
Olahraga diselesaikan

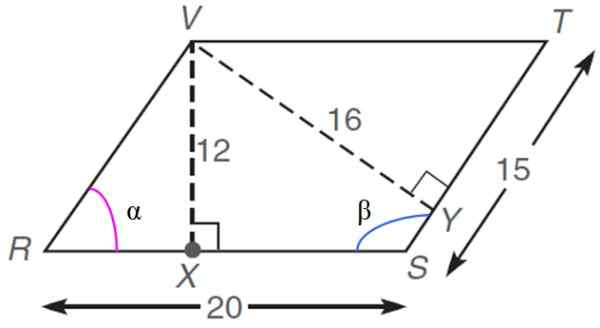
Dalam rhomboid berikut, yang dimensinya diberikan dalam unit sewenang -wenang atau.ke., menemukan:

a) nilai perimeter

b) area tersebut

c) Sudut internal α dan β

d) Panjang segmen RX

e) ukuran masing -masing diagonal

Solusi untuk

Perimeter P adalah:

P = 2 (a + b)

Kami mengidentifikasi nilai -nilai A dan B:

A = 20

B = 15

Kami mengganti rumus dan menghitung:

P = 2. (20 + 15) = 70 u.ke.

Solusi b

Diagram memberikan tinggi h = 12 u.A, oleh karena itu area tersebut dapat dihitung dengan rumus:

A = a x h

A = 20 x 12 u.ke.² = 240 u.ke.²

Terlepas dari unit yang dipilih untuk mengukur sisi dan tinggi, area tersebut selalu diekspresikan dalam unit kuadrat.

Hasil yang sama jika Anda mendapatkan saat menghitung area dengan ketinggian rhomboid lainnya, yang bernilai 16 u.ke. Memang:

A = 16 x 15 u.ke.² = 240 u.ke.²

Solusi c

Sudut α dapat dihitung melalui:

Itu dapat melayani Anda: langkah -langkah posisi, kecenderungan sentral dan dispersi

h = b. dosa α

Karena nilai H dan B diketahui, oleh karena itu:

α = arcsen (h/b) = arcsen (12/15) = 53.13

Mengingat bahwa sudut α dan β bersifat tambahan, dipenuhi:

α + β = 180º ⇒ β = 180 - 53.13 = 126.87º

Solusi d

Panjang segmen RX mudah dihitung, karena ada informasi yang cukup untuk menemukannya. Misalnya melalui:

Rx = rv . cos α = 15 . Cos 53.13th u.ke. = 9 u.ke.

Juga melalui teorema Pythagoras melalui segitiga persegi panjang dari sisi 15 dan 12 U.ke:

(RV)² = (Rx)² + H²

Membersihkan panjang segmen bunga:

Rx = √ [(rv)² - H²] = √ [15² - 12²] = √81 = 9

Solusi e

Ukuran salah satu diagonal, misalnya diagonal yang bergabung dengan simpul R dan T, yang merupakan diagonal utama, diberikan oleh teorema kosinus, seperti yang dijelaskan sebelumnya, jadi kami mengganti nilai di sana:

D_M = √ (20² + 25² - 2. dua puluh. limabelas .Cos 126.87º) = 37.22 u.ke.

Untuk diagonal minor:

D_M = √ (20² + 25² - 2. dua puluh. limabelas .Cos 53.13) = 25.79 u.ke.

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Baldor, a. 1973. Geometri dan Trigonometri. Editorial Budaya Amerika Tengah.
3. DAN. KE. 2003. Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
4. Jiménez, r. 2010. Matematika II. Geometri dan Trigonometri. Edisi kedua. Prentice Hall.
5. Poligon biasa. Pulih dari: sobat.rekayasa.USAC.Edu.GT.
6. Rumus alam semesta. Genjang. Pulih dari: universoformulas.com.
7. Wikipedia. Genjang. Pulih dari: is.Wikipedia.org.