Karakteristik variabel kontinu, contoh dan latihan

Itu Variabel kontinu Ini adalah salah satu yang dapat mengambil jumlah nilai numerik yang tak terbatas antara dua nilai yang diberikan, bahkan jika kedua nilai tersebut ditutup secara sewenang -wenang. Mereka digunakan untuk menggambarkan atribut yang dapat diukur; Misalnya tinggi dan berat badan. Nilai yang diambil oleh variabel kontinu dapat berupa bilangan rasional, bilangan real atau bilangan kompleks, meskipun kasus terakhir ini lebih jarang dalam statistik. 

Karakteristik utama dari variabel kontinu adalah bahwa antara dua nilai rasional atau nyata selalu dapat ditemukan, dan antara yang lain dan yang pertama dapat menemukan nilai lain, dan dengan demikian tanpa batas waktu.

Gambar 1. Kurva mewakili distribusi kontinu dan bilah yang bijaksana. Sumber: Pixabay

Sebagai contoh, misalkan variabel berat dalam kelompok di mana berat terbesar memiliki 95 kg dan berat 48 kg terendah; Itu akan menjadi kisaran variabel dan jumlah nilai yang mungkin tidak terbatas.

Misalnya antara 50,00 kg dan 50,10 kg mungkin 50,01. Tetapi antara 50,00 dan 50,01 ukurannya mungkin 50.005. Itu adalah variabel kontinu. Di sisi lain, jika dalam ukuran berat yang mungkin dilakukan, akurasi desimal tunggal ditetapkan maka variabel yang digunakan akan bijaksana.

Variabel kontinu milik kategori variabel kuantitatif, karena mereka memiliki nilai numerik yang terkait. Dengan nilai numerik ini dimungkinkan untuk melakukan operasi matematika mulai dari aritmatika hingga metode perhitungan infinitesimal. 

[TOC]

Contoh

Sebagian besar variabel fisika adalah variabel kontinu, di antaranya dapat kita beri nama: panjang, waktu, kecepatan, akselerasi, energi, suhu dan lainnya.

Variabel kontinu dan variabel diskrit

Dalam statistik, berbagai jenis variabel dapat didefinisikan, baik kualitatif maupun kuantitatif. Variabel kontinu termasuk dalam kategori terakhir ini. Dengan mereka adalah mungkin untuk melakukan operasi aritmatika dan perhitungan.

Misalnya variabel H, sesuai dengan orang dengan tinggi antara 1,50 m dan 1,95 m, ini adalah variabel kontinu. 

Mari kita bandingkan variabel ini dengan yang lain ini: berapa kali yang mahal dalam peluncuran mata uang, yang akan kita hubungi N.

Variabel N Anda dapat mengambil nilai antara 0 dan Infinity, namun N Ini bukan variabel kontinu karena tidak dapat mengambil nilai 1.3 atau 1.5, karena antara nilai 1 dan 2 tidak ada yang lain. Ini adalah contoh dari Variabel diskrit.

Latihan variabel kontinu

Pertimbangkan contoh berikut: Mesin menghasilkan kecocokan fosfor dan bungkus di dalam kotaknya. Dua variabel statistik didefinisikan:

Dapat melayani Anda: Proses Isobarik: Rumus, Persamaan, Eksperimen, Latihan

Variabel 1: l = panjang plose.

Variabel 2: n = Jumlah babi per kotak.

Panjang pencocokan nominal adalah 5,0 cm dengan toleransi 0,1 cm. Jumlah babi per kotak adalah 50 dengan toleransi 3.

a) Tunjukkan kisaran nilai yang dapat diambil L Dan N.

b) Berapa banyak nilai yang dapat Anda ambil L?

c) Berapa banyak nilai yang dapat Anda ambil N?

Katakanlah dalam setiap kasus jika itu adalah variabel yang bijaksana atau kontinu.

Larutan

Nilai -nilai L Mereka dipahami dalam interval [5,0-0.1; 5.0+0.1]; artinya nilai L adalah dalam interval [4,9 cm; 5.1 cm] dan variabel L Anda dapat mengambil nilai tak terbatas antara kedua langkah ini. Itu kemudian variabel kontinu.

Nilai variabel N berada dalam interval [47; 53]. Variabel N Hanya dapat mengambil 6 nilai yang mungkin dalam interval toleransi, itu adalah variabel yang bijaksana.

Latihan distribusi kemungkinan

Jika selain kontinu, nilai -nilai yang diambil oleh variabel telah mengaitkan probabilitas kejadian tertentu, maka itu adalah a Variabel acak kontinu. Sangat penting untuk membedakan apakah variabel tersebut bijaksana atau kontinu, karena model probabilistik yang berlaku satu sama lain berbeda.

Variabel acak kontinu sepenuhnya ditentukan ketika nilai yang dapat mereka asumsikan diketahui, dan probabilitas bahwa masing -masing harus terjadi.

-Latihan 1 probabilitas

Pabrik yang cocok membuat mereka sedemikian rupa sehingga panjang tongkat selalu antara nilai 4,9 cm dan 5,1 cm, dan nol dari nilai -nilai ini. Ada kemungkinan mendapatkan tongkat yang berukuran antara 5,00 dan 5,05 cm, meskipun kami juga bisa mengekstrak salah satu dari 5.0003 cm. Apakah nilai -nilai ini sama -sama mungkin?.

Dapat melayani Anda: kepadatan relatif: perhitungan, contoh, latihan

Larutan

Misalkan kepadatan probabilitas seragam. Selanjutnya, kemungkinan menemukan fosfor dengan panjang tertentu terdaftar:

-Bahwa fosfor berada dalam kisaran [4,9; 5,1] memiliki probabilitas = 1 (atau 100%), karena mesin tidak cocok dari nilai -nilai tersebut.

-Menemukan fosfor yang antara 4,9 dan 5,0 memiliki probabilitas = ½ = 0,5 (50%), karena itu adalah setengah dari kisaran panjang.

-Dan probabilitas bahwa kecocokan memiliki panjang antara 5,0 dan 5,1 juga 0,5 (50%)

-Diketahui bahwa tidak ada tongkat fosfor yang memiliki panjang antara 5.0 dan 5.2. Probabilitas: nol (0%).

Probabilitas menemukan tongkat dalam kisaran tertentu

Sekarang mari kita amati probabilitas berikut untuk mendapatkan tongkat yang panjangnya antara L₁ dan saya₂:

 P = (l₂ -l₁) /(L_Max - L_Min)

-P bahwa kecocokan memiliki panjang antara 5,00 dan 5,05 dilambangkan sebagai P ([5.00; 5.05]):

P ([5.00; 5.05]) = (5.05 - 5.00)/(5.1 - 4.9) = 0.05/0.2 = ¼ = 0.25 (25%)

-P bahwa Cerrillo memiliki panjang antara 5.00 dan 5.01 adalah:

P ([5.00; 5.01]) = (5.00 - 5.01)/(5.1 - 4.9) = 0.01/0.2 = 1/20 = 0.05 (5 %)

-P bahwa Cerrillo memiliki panjang antara 5.000 dan 5.001 bahkan lebih rendah:

P (5.000; 5.001) = 0,001/0,2 = 1/200 = 0,005 (0,5%)

Jika kita terus mengurangi interval untuk mendekati semakin banyak ke 5,00, probabilitas bahwa tongkat memiliki persis 5,00 cm adalah nol (0%). Yang kami miliki adalah probabilitas menemukan kecocokan dalam kisaran tertentu.

Probabilitas menemukan beberapa tongkat dalam kisaran tertentu

Jika peristiwa tersebut independen, probabilitas bahwa dua tongkat berada dalam kisaran tertentu adalah produk dari probabilitas mereka.

-Probabilitas bahwa dua tongkat adalah antara 5,0 dan 5,1 adalah 0,5*0,5 = 0,25 (0,25%)

-Probabilitas bahwa 50 tongkat adalah antara 5,0 dan 5,1 adalah (0,5)^50 = 9 × 10^-16, yang hampir nol.

-Probabilitas bahwa 50 tongkat adalah antara 4,9 dan 5.1 adalah (1)^50 = 1 (100%)

-Latihan 2 probabilitas

Dalam contoh sebelumnya, asumsi dibuat bahwa probabilitas seragam dalam interval yang diberikan, namun tidak selalu demikian.

Dapat melayani Anda: Tekanan Hidrostatik: Formula, Perhitungan, Contoh, Latihan

Dalam kasus mesin nyata yang menghasilkan tongkat, kemungkinan bahwa tongkat berada dalam nilai sentral lebih besar daripada di salah satu nilai ekstrem. Dari sudut pandang matematika ini dimodelkan dengan fungsi f (x) yang dikenal sebagai kepadatan probabilitas.

Probabilitas bahwa ukurannya adalah antara A dan B dihitung dengan integral yang ditentukan dari fungsi f (x) antara A dan B. 

Sebagai contoh, misalkan kita ingin menemukan fungsi f (x), yang mewakili distribusi seragam antara nilai 4.9 dan 5.1 dari Latihan 1. 

Jika distribusi probabilitas seragam, maka f (x) sama dengan konstanta C, yang ditentukan mengambil integral antara 4,9 dan 5,1 c. Karena integral ini adalah probabilitas, jadi hasilnya harus 1.

Gambar 2. Kepadatan probabilitas seragam. (Elaborasi sendiri)

Yang berarti bahwa C bernilai 1/0,2 = 5. Dengan kata lain, fungsi kepadatan probabilitas yang seragam adalah f (x) = 5 jika 4.9≤x≤5.1 dan 0 dari kisaran ini. Gambar 2 menunjukkan fungsi kepadatan probabilitas yang seragam.

Perhatikan seperti dalam interval lebar yang sama (misalnya 0,02) probabilitasnya sama di tengah seperti pada akhir rentang variabel kontinu L (Panjang acar).

Model yang lebih realistis akan menjadi fungsi kepadatan probabilitas sebagai berikut:

-f (x) = -750 ((x-5.0)^2-0.01) jika 4.9≤x≤5,1

-0 Di luar kisaran ini 

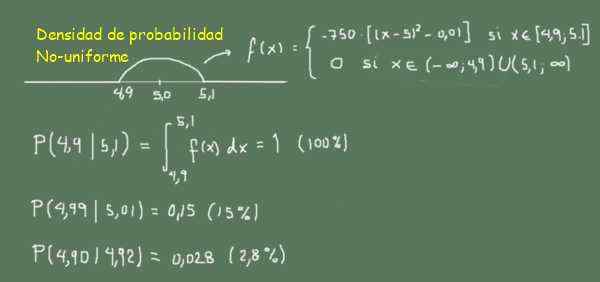Gambar 3. Fungsi kepadatan probabilitas non -uniform. (Elaborasi sendiri)

Pada Gambar 3 dapat diamati sebagai probabilitas menemukan tongkat antara 4,99 dan 5,01 (lebar 0,02) lebih besar dari menemukan tongkat antara 4,90 dan 4,92 (lebar 0,02)

Referensi

1. Dinov, Ivo. Variabel acak diskrit dan distribusi probabilitas. Pulih dari: stat.UCLA.Edu
2. Variabel acak diskrit dan kontinu. Pulih dari: ocw.mit.Edu
3. Variabel acak diskrit dan distribusi probabilitas. Pulih dari: beranda.DDMS.Uiowa.Edu
4. H. Peshro. Pengantar probabilitas. Pulih dari: kursus probabilitas.com
5. Mendenhall, w. 1978. Statistik untuk Administrasi dan Ekonomi. Ibero -American Editorial Group. 103-106.
6. Masalah variabel acak dan model probabilitas. Dipulihkan dari: UGR.adalah.
7. Wikipedia. Variabel kontinu. Pulih dari Wikipedia.com
8. Wikipedia. Variabel statistik. Pulih dari Wikipedia.com.