Karakteristik, contoh dan latihan vektor bersamaan

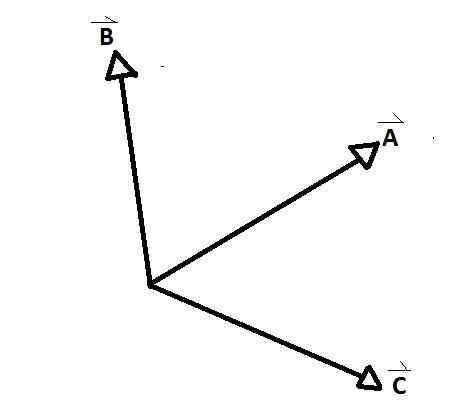
Itu Vektor bersamaan Mereka adalah kelompok vektor yang kapaknya bertepatan pada satu titik, membentuk di antara masing -masing pasangan dari mereka yang memiliki sudut internal dan eksternal. Contoh yang jelas diamati pada gambar yang lebih rendah, di mana a, b dan c adalah vektor bersamaan satu sama lain.

D dan E tidak seperti yang lain tidak. Ada sudut yang terbentuk di antara vektor bersamaan AB, AC dan CB. Sudut hubungan antar vektor disebut.

[TOC]

Karakteristik

-Mereka memiliki titik yang sama, yang bertepatan dengan asal mereka: semua besarnya vektor bersamaan mulai dari titik yang sama ke masing -masing ekstrem.

-Asal dianggap sebagai titik tindakan vektor: titik tindakan harus ditetapkan yang akan secara langsung dipengaruhi oleh masing -masing vektor bersamaan.

-Domain Anda di pesawat dan ruang R² dan r³ masing -masing: vektor bersamaan bebas untuk menutupi seluruh ruang geometris.

-Memungkinkan notasi yang berbeda dalam kelompok vektor yang sama. Menurut cabang studi, notasi yang berbeda hadir dalam operasi dengan vektor.

Jenis vektor

Cabang vektor memiliki beberapa subdivisi, di antara beberapa mereka dapat ditunjuk: paralel, tegak lurus, coplanario, yang sesuai, berlawanan dan kesatuan. Vektor bersamaan muncul di daftar ini dan seperti semua yang sebelumnya ditunjuk, mereka memiliki banyak aplikasi dalam ilmu yang berbeda.

Mereka sangat umum dalam studi vektor, karena mereka mewakili generalisasi yang menguntungkan dalam operasi dengan mereka. Baik di pesawat dan di luar angkasa, vektor bersamaan adalah untuk penggunaan saat ini untuk representasi elemen yang berbeda dan mempelajari pengaruhnya terhadap sistem tertentu.

Notasi vektor

Ada berbagai cara untuk mewakili elemen vektor. Yang utama dan paling terkenal adalah:

Cartesian

Diusulkan oleh pendekatan matematika yang sama ini, menunjukkan vektor dengan daftar yang sesuai dengan besaran masing -masing sumbu (x, y, z)

A: (1, 1, -1) Ruang A: (1, 1) Rencana

Kutub

Mereka hanya berfungsi untuk menunjukkan vektor di pesawat, meskipun dalam perhitungan integral komponen kedalaman ditetapkan. Ini terdiri dengan besarnya linear R dan sudut sehubungan dengan sumbu kutub Ɵ.

Dapat melayani Anda: statistik inferensial: sejarah, karakteristik, untuk apa, contohnya

A: (3, 45⁰ ) Rencana A: (2, 45⁰ , 3) Ruang

Analitik

Tentukan besaran vektor melalui versor. Versor (R&E + K) mewakili vektor unit yang sesuai dengan sumbu X, y Dan

A: 3i + 2j - 3k

Bulat

Mereka mirip dengan notasi kutub, tetapi dengan penambahan sudut kedua yang menyapu pesawat Xy dilambangkan oleh δ.

A: (4, 60^{salah satu} , π/4)

Operasi dengan vektor bersamaan

Vektor bersamaan sebagian besar digunakan untuk mendefinisikan operasi antar vektor, karena lebih mudah untuk membandingkan unsur -unsur vektor ketika terjadi dengan cara yang bersamaan.

Jumlah (A + B)

Jumlah vektor bersamaan bertujuan untuk menemukan vektor yang dihasilkan V_R. Yang, menurut cabang studi, sesuai dengan tindakan akhir

Misalnya: 3 string diikat a, b, c ke kotak, setiap ujung tali ada di tangan subjek. Masing -masing dari 3 subjek harus menarik tali ke arah selain 2 lainnya.

A: (AX, AY, AZ) B: (BX, oleh, BZ) C: (CX, CY, CZ)

A+b+c = (ax+bx+cx; ay+oleh+cy; az+bz+cz) = V_R

Kotak hanya bisa bergerak dalam satu arah, oleh karena itu V_R akan menunjukkan arah dan rasa perpindahan kotak.

Perbedaan (A - B)

Ada banyak kriteria mengenai perbedaan antara vektor, banyak penulis memilih untuk mengecualikannya dan mengklaim bahwa hanya jumlah antara vektor yang ditentukan, di mana perbedaannya adalah jumlah dari vektor yang berlawanan. Yang benar adalah bahwa vektor aljabar dapat dikurangi.

A: (AX, AY, AZ) B: (BX, oleh, BZ)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]

Produk skalar (a . B)

Juga dikenal sebagai produk Punto, menghasilkan nilai skalar yang dapat dikaitkan dengan beberapa besaran menurut cabang penelitian.

Untuk geometri menunjukkan area jajaran genjang yang dibentuk oleh pasangan vektor bersamaan melalui metode jajaran genjang. Untuk fisika mekanis menentukan pekerjaan yang dilakukan oleh suatu kekuatan F Dengan menggerakkan tubuh dari jarak Δr.

Itu dapat melayani Anda: proporsionalitas majemuk: penjelasan, tiga aturan majemuk, latihan

ѡ = f . Δr

Seperti namanya, itu menghasilkan nilai skalar dan didefinisikan sebagai berikut:

Jadilah vektor a dan b

A: (AX, AY, AZ) B: (BX, oleh, BZ)

-Bentuk analitik:

( KE . B) = | a |.| B |.Cos θ

Di mana θ adalah sudut internal antara kedua vektor

-Bentuk Aljabar:

( KE . B) = (kapak.Bx + ay.oleh + az.BZ)

Produk Vektor (A X B)

Vektor atau produk titik antara dua vektor, mendefinisikan vektor ketiga C yang memiliki kualitas tegak lurus B Dan C. Dalam fisika menentukan torsi vektor τ Elemen dasar dinamika rotasi.

-Bentuk analitik:

| A X B | = | A |.| B |.Dosa θ

-Bentuk Aljabar:

(A x b) = = (Kapak . oleh - ay . bx)- (kapak . BZ - AZ . bx) J + (Kapak . oleh - ay . bx) k

-Gerakan Relatif: R_A/b

Dasar relativitas adalah gerakan relatif dan vektor bersamaan adalah dasar dari gerakan relatif. Anda dapat menyimpulkan posisi, kecepatan, dan percepatan relatif dengan menerapkan urutan ide berikut.

R _A/b = r_KE - R_B    ; Posisi relatif tentang b

v _A/b = v_KE - v_B  ; Kecepatan relatif terhadap B

ke _A/b = a_KE - ke_B  ; Akselerasi Relatif Hormat terhadap B

Contoh: latihan terpecahkan

Latihan 1

Biarkan vektor bersamaan.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Tentukan vektor yang dihasilkan V_R = 2a - 3b + c

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_R = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_R = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1)))

V_R = (-15, -11, 17)

-Tentukan produk skalar (a . C)

( KE . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

( KE . C) = 3

-Hitung sudut antara A dan C

( KE . C) = | a |.| C |.Cos θ di mana θ adalah sudut terpendek di antara vektor

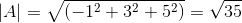
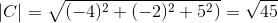
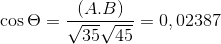
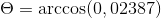
θ = 88.63⁰

 -Temukan vektor tegak lurus terhadap a dan b

Untuk ini perlu untuk menentukan produk vektor antara (-1, 3, 5) dan (3, 5, -2). Seperti yang dijelaskan sebelumnya, matriks 3 x 3 dibangun di mana baris pertama terdiri dari daftar vektor unit (i, j, k). Kemudian baris ke -2 dan ke -3 terdiri dari vektor untuk dioperasikan, menghormati pesanan operasional.

Dapat melayani Anda: notasi desimal

(A x b) = = [(-1) . 5 - (3 . 3)] yo  - [(-1) . (-2) - (5 . 3)] J + [(-1) . 5 - (3 . 3)] k

(A x b) = (-5 - 9) yo - (2 - 15) J + (-5 - 9) k         

(A x b) =  -14 I + 13 J - 14 K

Latihan 2 

Biarkan v_ke dan v_B Vektor kecepatan a dan b masing -masing. Hitung kecepatan B dari a.

V_ke = (3, -1, 5) v_B = (2, 5, -3)

Dalam hal ini, kecepatan relatif B diminta dari V_B/a

V_B/a = V_B - V_KE

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Ini adalah vektor veloc B yang terlihat dari a. Di mana vektor baru kecepatan B dijelaskan dengan merujuk pengamat yang diposisikan dalam a dan bergerak dengan kecepatan a.

Latihan yang diusulkan

1-konstruksi 3 vektor A, B dan C yang bersamaan dan berhubungan 3 operasi di antara mereka melalui latihan praktis.

2 -Vektor A: (-2, 4, -11), B: (1, -6, 9) dan C: (-2, -1, 10). Temukan vektor tegak lurus ke: A dan B, C dan B, Jumlah A + B + C.

Vektor 4-determine 3 yang tegak lurus satu sama lain, tanpa memperhitungkan sumbu koordinat.

5-Tentukan pekerjaan yang dilakukan oleh kekuatan yang mengangkat blok massa 5 kg, dari bagian bawah sumur 20 m.

Aljabar 6-Swamker bahwa pengurangan vektor sama dengan jumlah vektor yang berlawanan. Membenarkan postulat Anda.

7-denote vektor dalam semua notasi yang dikembangkan dalam artikel ini. (Cartesian, Polar, Analytics, dan Spherical).

8-The Magnetic Forces diberikan pada magnet yang bertumpu di atas meja, diberikan oleh vektor-vektor berikut; V: (5, 3, -2), t: (4, 7, 9), h: (-3, 5, -4). Tentukan ke arah mana magnet akan bergerak jika semua gaya magnetik bertindak pada saat yang sama.

Referensi

1. Geometri dan transformasi Euclidean. Clayton w. Menghindari. Couer Corporation, 1 Jan. 2004
2. Cara memecahkan masalah matematika l. Moiseiwitsch. Couer Corporation, 10 Apr. 2013
3. Konsep dasar geometri. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4 Okt. 2012
4. Vektor. Rocío Navarro Lacoba, 7 Juni. 2014
5. Aljabar linier. Bernard Kolman, David R. BUKIT. Pearson Education, 2006