Vektor unit karakteristik, cara mengeluarkannya, contoh

Itu Vektor unit adalah mereka yang modul, besarnya atau ukurannya sama dengan nilai numerik. Vektor unit berguna untuk menunjukkan arah vektor non -unit lainnya.

Ingatlah bahwa vektor adalah entitas matematika yang secara matematis mewakili besaran fisik yang bergantung pada arah, seperti kekuatan, kecepatan, akselerasi dan lainnya.

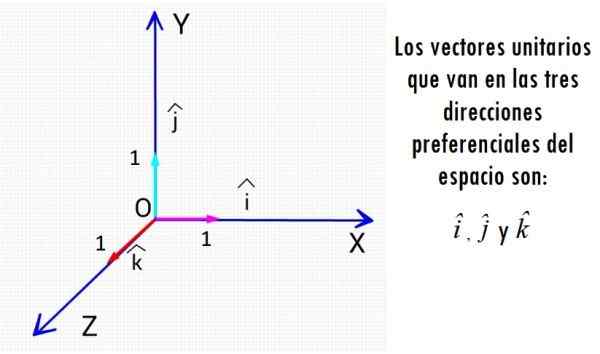
Vektor unit paling terkenal adalah tiga vektor yang masuk ke arah kapak cartesius. Sumber: f. Zapata.

Terlepas dari besarnya fisik yang terkait, vektor unit adalah entitas yang tidak memiliki unit ukuran dan ukurannya selalu 1, angka murni.

Misalnya, kecepatan partikel yang bergerak pada 3 m/s dan masuk ke arah positif sumbu X Cartesian dilambangkan: v = (3 m/s) yo, di mana huruf tebal digunakan untuk menunjukkan jumlah vektor. Dalam contoh ini modul v Ini adalah 3 m/s dan modul vektor unit yo adalah 1 (tanpa unit).

[TOC]

Modul, arah dan makna

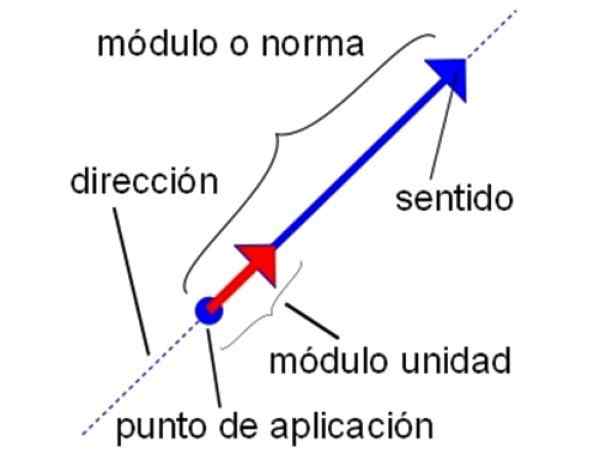
Diberi yang penting. Pada saat mewakili jumlah vektor, perlu untuk menunjukkan secara jelas aspek -aspek ini.

Sekarang, vektor unit dapat memiliki arah apa pun dan makna yang lebih disukai, tetapi besarnya harus selalu sama dengan 1.

Vektor unit digunakan untuk menunjukkan alamat pribadi di ruang atau di pesawat. Jika, misalnya, kita perlu bekerja dengan semua kekuatan yang bertindak di sepanjang sumbu horizontal, karena vektor satuan ke arah itu membantu kita membedakan kekuatan -kekuatan ini dari orang lain yang diarahkan ke arah yang berbeda.

Dan untuk membedakan mereka dari vektor non -unit, tebal biasanya digunakan dalam cetakan dan menempatkan aksen sirkumfleks di atas, misalnya:

Itu dapat melayani Anda: Teori Stasioner Negara: Sejarah, Penjelasan, Berita

Untuk lirik tulisan tangan, itu cukup untuk menempatkan sirkumflejo untuk memahami bahwa itu adalah vektor unit.

Karakteristik vektor unit

Secara matematis vektor unit:

Ini adalah elemen yang termasuk dalam ruang vektor ℛ dimensi n, sehingga |v| = 1, di mana bilah berarti "modul".

Jadi kita bisa menetapkannya:

-Modul vektor kesatuan selalu 1, tidak masalah jika itu adalah kekuatan, kecepatan atau vektor lainnya.

-Vektor unit memiliki arah tertentu, serta arah, seperti vektor unit dalam arah vertikal, yang mungkin masuk akal naik atau turun.

-Vektor unit memiliki titik asal. Ketika diwakili oleh sistem koordinat Cartesian, titik tersebut bertepatan dengan asal sistem: (0,0) jika itu adalah pesawat atau (0,0,0) jika vektor berada dalam ruang tiga -dimensi.

Karakteristik vektor unit. Sumber: Wikimedia Commons.

-Juga dengan vektor unit, semua operasi jumlah jumlah, pengurangan dan vektor yang dibuat oleh vektor reguler dapat dilakukan. Oleh karena itu valid untuk mengalikan vektor unit dengan skalar, serta melaksanakan produk titik dan produk silang.

-Dengan vektor satuan ke arah tertentu, vektor lain juga dapat diekspresikan yang juga berorientasi ke arah itu.

Vektor unit di luar angkasa

Untuk mengekspresikan vektor apa pun di ruang angkasa atau di pesawat, Anda dapat menggunakan satu set vektor kesatuan yang tegak lurus satu sama lain, yang membentuk basis ortormal. Masing -masing dari tiga arah ruang preferensial memiliki vektor unitnya sendiri.

Mari kita kembali ke contoh gaya yang diarahkan sepanjang sumbu horizontal. Ini adalah sumbu x, yang memiliki dua kemungkinan: arah ke kanan dan arah ke kiri. Misalkan ada vektor unit pada sumbu x dan diarahkan ke kanan, yang dapat kita tunjukkan melalui salah satu bentuk ini:

Dapat melayani Anda: Model Atom Thomson: Karakteristik, Deposulat, Partikel Subatomik

Salah satu dari mereka valid. Sekarang, anggaplah kekuatan F₁ Besar 5 N di sepanjang sumbu ini dan diarahkan ke kanan, gaya seperti itu dapat dinyatakan sebagai:

Jika gaya diarahkan sepanjang sumbu x tetapi dalam arah yang berlawanan, yaitu, di sebelah kiri, maka tanda negatif dapat digunakan untuk menetapkan perbedaan ini.

Misalnya, gaya 8 N besarnya, yang terletak pada sumbu X dan diarahkan ke kiri akan seperti ini:

Atau lebih:

Dan untuk vektor yang tidak diarahkan di sepanjang kapak Cartesian, ada juga cara untuk mewakili mereka dalam hal vektor unit ortogonal, melalui komponen Cartesian mereka.

Cara menghapus/menghitung vektor unit?

Untuk menghitung vektor unit ke arah vektor sewenang -wenang v, Formula berikut diterapkan:

Di mana:

Itu adalah modul atau besarnya vektor v, yang kuadrat dihitung seperti ini:

|v|² = (v_X)² +  (v_Dan)²+  (v_z)²

Vektor sewenang -wenang dalam hal vektor unit

Atau vektor v Itu dapat dinyatakan sebagai berikut:

Yaitu, produk modulnya dengan vektor unit yang sesuai. Inilah yang dilakukan sebelumnya, ketika berbicara tentang gaya 5 n besarnya diarahkan sepanjang sumbu x positif.

Representasi Grafik

Secara grafis, apa yang dikatakan terlihat pada gambar ini, di mana vektor v Warnanya biru dan vektor unit yang sesuai dalam arahnya berwarna merah.

Dalam contoh ini, vektor v Ini memiliki besarnya lebih besar dari vektor unit, tetapi penjelasannya bahkan valid jika ini tidak terjadi. Dengan kata lain, kita dapat memiliki vektor yang misalnya 0.25 kali vektor unit.

Dapat melayani Anda: berat (fisik): perhitungan, unit, contoh, latihan

Contoh vektor unit

Vektor unit tegak lurus i, j dan k

Seperti yang telah kita lihat sebelumnya, vektor unit tegak lurus yo, J Dan k Mereka sangat berguna untuk mewakili vektor lain di pesawat atau ruang, dan melakukan operasi vektor. Dalam hal vektor tersebut, vektor V yang sewenang -wenang direpresentasikan sebagai:

v = v_X yo + v_Dan J + v_z k

Dimana v_X, v_Dan dan v_z adalah komponen persegi panjang dari vektor v, yang merupakan pendakian -bold tidak digunakan untuk mewakili mereka dalam teks cetak-.

Hukum Coulomb

Vektor kesatuan sering muncul dalam fisika. Di sana kami memiliki hukum Coulomb, misalnya, yang secara kuantitatif menggambarkan interaksi antara dua muatan listrik spesifik.

Itu menunjukkan bahwa kekuatan F ketertarikan atau tolakan antara beban ini sebanding dengan produknya, berbanding terbalik dengan kuadrat jarak yang memisahkannya dan diarahkan ke arah vektor unit yang bergabung dengan beban.

Vektor ini biasanya diwakili oleh:

Dan hukum Coulomb seperti ini, dalam bentuk vektor:

Di mana k Itu adalah konstanta elektrostatik, Q₁ Dan Q₂ Mereka adalah beban dan R Itu adalah jarak yang memisahkan mereka.

Olahraga diselesaikan

Temukan vektor unit ke arah vektor v = 5yo + 4J -8k, Diberikan dalam unit sewenang -wenang.

Larutan

Definisi vektor kesatuan di atas diterapkan di atas:

Tetapi pertama -tama Anda harus menghitung modul vektor, yang memiliki tiga komponen, ditentukan oleh:

|v|² = (v_X)² +  (v_Dan)² +  (v_z)²

Tetap:

|v|² = (5)² +  (4)² +  (-8)²= 25 + 16 + 64 = 105

Oleh karena itu modul v adalah:

|v| = √105

Vektor kesatuan yang dicari adalah:

Itu akhirnya menuntun kita ke:

v = 0.488 yo + 0.390 J - 0.781 k

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Bedford, 2000. KE. Mekanika untuk Teknik: Statis. Addison Wesley.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
5. Resnick, r. (1999). Fisik. Vol. 1. Edisi ke -3. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V.