Karakteristik amplitudo gelombang, formula dan olahraga

Itu Amplitudo Gelombang Ini adalah perpindahan maksimum yang dialami oleh titik dalam gelombang sehubungan dengan posisi kesetimbangan. Gelombang terwujud di mana -mana dan banyak cara di dunia di sekitar kita: di lautan, dalam suara dan di tali instrumen yang menghasilkannya, dalam cahaya, di permukaan bumi dan banyak lagi.

Salah satu cara untuk menghasilkan gelombang dan mempelajari perilakunya adalah mengamati getaran tali yang memiliki ujung tetap. Dengan menghasilkan gangguan di ujung yang lain, setiap partikel tali berosilasi dan dengan itu energi gangguan ditransmisikan dalam bentuk suksesi pulsa di seluruh.

Gelombang terwujud dalam banyak hal di alam. Sumber: Pixabay.

Saat energi menyebar, tali yang seharusnya sangat elastis, mengadopsi bentuk sinusoidal khas dengan punggung bukit dan lembah yang ditunjukkan pada gambar yang muncul di bawah ini di bagian berikut.

[TOC]

Karakteristik dan makna amplitudo gelombang

Amplitudo A adalah jarak antara lambang dan sumbu referensi atau level 0. Jika lebih disukai, antara lembah dan sumbu referensi. Jika gangguan pada tali ringan, amplitudo A kecil. Jika sebaliknya gangguan itu intens, amplitudo akan lebih besar.

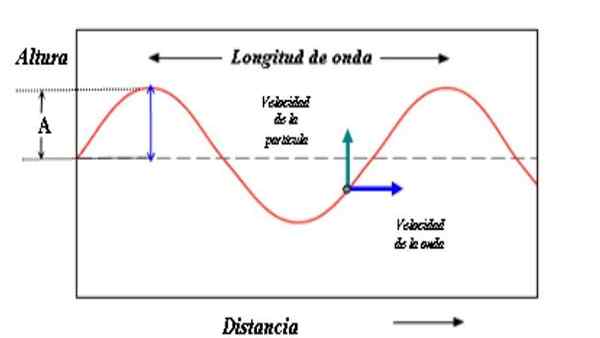Model untuk menggambarkan gelombang terdiri dari kurva sinusoidal. Amplitudo gelombang adalah jarak antara lambang atau lembah dan sumbu referensi. Sumber: Paco [CC BY-SA 3.0 (http: // createveCommons.Org/lisensi/by-sa/3.0/]]

Nilai amplitudo juga merupakan ukuran energi yang memakai gelombang. Intuitif bahwa amplitudo besar dikaitkan dengan energi yang lebih besar.

Faktanya energi sebanding dengan kuadrat amplitudo, yang dinyatakan secara matematis adalah:

I ∝A²

Dapat melayani Anda: induktansi timbal balik: formula/koefisien, aplikasi, latihan

Di mana saya adalah intensitas gelombang, pada gilirannya terkait dengan energi.

Jenis gelombang yang diproduksi dalam contoh tali, termasuk dalam kategori gelombang mekanik. Fitur penting adalah bahwa setiap partikel pada tali selalu tetap sangat dekat dengan posisi keseimbangannya.

Partikel tidak bergerak atau bergerak melalui tali. Mereka berkisar ke atas dan ke bawah. Ini ditunjukkan dalam skema atas dengan panah hijau, namun gelombang bersama energinya, bergerak dari kiri ke kanan (panah biru).

Gelombang yang menyebar di dalam air memberikan bukti yang diperlukan untuk meyakinkan diri mereka sendiri tentang hal ini. Mengamati pergerakan lembaran yang telah jatuh ke dalam kolam dapat dilihat bahwa dia hanya berosilasi yang menyertai pergerakan air. Tidak terlalu jauh, setidaknya jelas, bahwa ada kekuatan lain yang memberikan gerakan lain.

Model gelombang yang ditunjukkan pada gambar terdiri dari pola berulang di mana jarak antara dua punggung adalah panjang gelombang λ. Jika Anda mau, panjang gelombang juga memisahkan dua titik identik dari gelombang, bahkan saat mereka tidak berada di puncak.

Deskripsi matematika dari gelombang

Secara alami, gelombang dapat dijelaskan dengan fungsi matematika. Fungsi periodik seperti sinus dan kosinus adalah yang ideal untuk tugas, apakah Anda ingin mewakili gelombang baik dalam ruang maupun dalam waktu.

Jika kita memanggil sumbu vertikal pada gambar dan sumbu horizontal kita menyebutnya "t", maka perilaku gelombang dari waktu ke waktu diekspresikan oleh:

y = a cos (ωt + δ)

Untuk gerakan ideal ini, setiap partikel tali berosilasi dengan gerakan harmonik sederhana, yang berasal berkat kekuatan yang berbanding lurus dengan perpindahan yang dilakukan oleh partikel tersebut.

Dapat melayani Anda: Dirac Jordan Atomic Model: Karakteristik dan Deposulat

Dalam persamaan yang diusulkan, a, Ω dan Δ adalah parameter yang menggambarkan gerakan, menjadi ke amplitudo sebelumnya didefinisikan sebagai perpindahan maksimum yang dialami oleh partikel sehubungan dengan sumbu referensi.

Argumen kosinus itu disebut Fase gerakan Dan Δ adalah konstanta fase, Apa fase saat t = 0. Fungsi cosinus dan fungsi sinus sesuai untuk menggambarkan gelombang, karena mereka hanya berbeda satu sama lain π/2.

Biasanya dimungkinkan untuk memilih t = 0 dengan Δ = 0 untuk menyederhanakan ekspresi, mendapatkan:

y = a cos (ωt)

Ketika gerakan berulang dalam ruang dan waktu, ada waktu yang khas periode t, didefinisikan sebagai waktu yang dibutuhkan untuk partikel untuk melakukan osilasi lengkap.

Deskripsi Gelombang dalam Waktu: Parameter Karakteristik

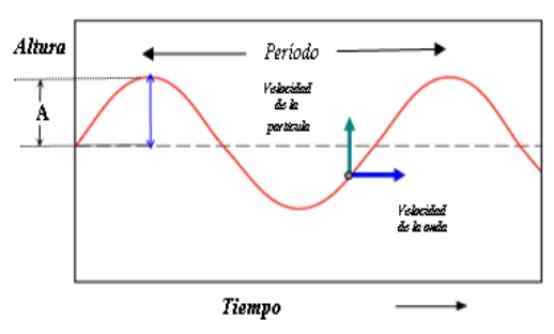Gambar ini menunjukkan deskripsi gelombang dalam waktu. Jarak antara punggung (atau lembah) sekarang sesuai dengan periode gelombang. Sumber: Paco [CC BY-SA 3.0 (http: // createveCommons.Org/lisensi/by-sa/3.0/]]

Sekarang, baik payudara dan kosinus mengulang nilainya ketika fase meningkat dalam nilai 2π, sehingga:

ωt = 2π → Ω = 2π /t

Ω dipanggil Frekuensi gerakan sudut Dan memiliki dimensi kebalikan waktu, menjadi unitnya di sistem internasional Radián / kedua atau kedua^-1.

Akhirnya Anda dapat mendefinisikan Frekuensi gerakan F, sebagai kebalikan atau timbal balik dari periode tersebut. Mewakili jumlah punggung per unit waktu, dalam hal ini:

F = 1/t

Ω = 2πf

Baik F dan Ω memiliki dimensi dan unit yang sama. Selain yang kedua^-1, yang disebut Hertz atau Hertzio, adalah hal biasa untuk didengar Revolusi per detik salah satu Revolusi per menit.

Kecepatan gelombang v, yang harus ditekankan bahwa itu tidak sama dengan yang dialami oleh partikel, itu dapat dengan mudah dihitung jika panjang gelombang λ dan frekuensi f diketahui:

Itu dapat melayani Anda: tubuh bercahaya: karakteristik dan bagaimana mereka menghasilkan cahaya sendiri

V = λf

Jika osilasi yang dialami oleh partikel adalah tipe harmonik sederhana, frekuensi sudut dan frekuensinya hanya bergantung pada sifat partikel berosilasi dan karakteristik sistem. Amplitudo gelombang tidak mempengaruhi parameter ini.

Misalnya, saat memainkan catatan musik pada gitar, catatan itu akan selalu memiliki nada yang sama meskipun disentuh dengan intensitas yang lebih besar atau lebih kecil, dengan cara ini akan selalu terdengar seperti dilakukan, meskipun terdengar lebih kuat atau lebih lembut komposisi, baik pada piano atau pada gitar.

Di alam, gelombang yang diangkut dalam lingkungan material ke segala arah dilemahkan karena energi menghilang. Untuk alasan ini amplitudo berkurang dengan kebalikan dari jarak R ke sumbernya, mungkin untuk menegaskan itu:

A∝1/r

Olahraga diselesaikan

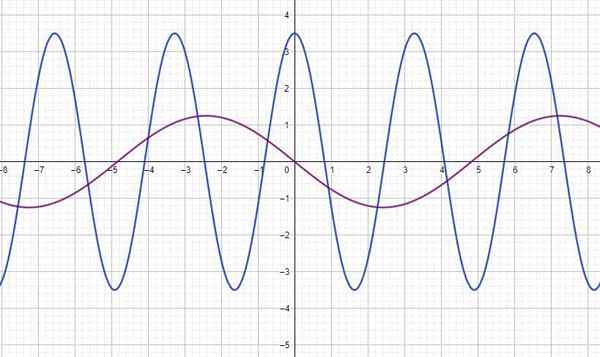
Gambar menunjukkan fungsi y (t) untuk dua gelombang, di mana Dan ada dalam meter dan T dalam hitungan detik. Untuk masing -masing temukan:

a) amplitudo

b) periode

c) frekuensi

d) Persamaan setiap gelombang dalam hal payudara atau cosenos.

Jawaban

a) Diukur langsung dari grafik, dengan bantuan kisi: Gelombang biru: A = 3.5m; Gelombang fuchsia: A = 1.25 m

b) Ini juga membaca grafik, menentukan pemisahan antara dua puncak atau lembah, berturut -turut: gelombang biru: t = 3.3 detik; Gelombang fuchsia t = 9.7 detik

c) Dihitung mengingat bahwa frekuensi adalah timbal balik dari periode: Gelombang biru: f = 0.302 Hz; Gelombang fuchsia: f = 0.103 Hz.

D) Gelombang Biru: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Gelombang fuchsia: y (t) = 1.25 dosa (0.65t) = 1.25 cos (0.65t+1.57)

Perhatikan bahwa gelombang fuchsia sudah ketinggalan zaman π/2 sehubungan dengan biru, dimungkinkan untuk mewakilinya dengan fungsi sinus. Atau mengungsi dari cosinus π/2.