Konsep analisis mesh, metode, contoh

Dia Analisis mesh Ini adalah teknik yang digunakan untuk menyelesaikan sirkuit listrik yang datar. Prosedur ini juga dapat muncul dalam literatur dengan nama metode dari arus sirkuit o Metode Arus mesh (atau loop).

Landasan metode analisis sirkuit listrik ini dan lainnya adalah dalam hukum Kirchhoff dan hukum Ohm. Hukum Kirchhoff pada gilirannya, adalah ekspresi dari dua prinsip konservasi yang sangat penting dalam fisika untuk sistem yang terisolasi: muatan listrik dan energi dipertahankan.

Gambar 1. Sirkuit adalah bagian dari perangkat yang tak terhitung banyaknya. Sumber: Pixabay.

Di satu sisi, muatan listrik terkait dengan arus, yang merupakan beban bergerak, sedangkan dalam sirkuit energi terkait dengan tegangan, yang merupakan agen yang bertanggung jawab untuk melakukan pekerjaan yang diperlukan untuk menjaga beban tetap bergerak.

Undang -undang ini, diterapkan pada sirkuit datar, menghasilkan satu set persamaan simultan yang harus diselesaikan untuk mendapatkan nilai arus atau tegangan.

Sistem persamaan dapat diselesaikan dengan teknik analitik yang sudah diketahui, seperti Aturan Cramer, yang membutuhkan perhitungan penentu untuk mendapatkan solusi sistem.

Bergantung pada jumlah persamaan, mereka diselesaikan dengan menggunakan kalkulator ilmiah atau perangkat lunak matematika. Di jaringan ada juga banyak opsi yang tersedia.

[TOC]

Istilah penting

Sebelum menjelaskan cara kerjanya, kita akan mulai dengan mendefinisikan istilah -istilah ini:

Cabang: Bagian yang berisi unsur sirkuit.

Node: titik yang menghubungkan dua atau lebih cabang.

Pita: Ini adalah bagian tertutup dari suatu sirkuit, yang dimulai dan berakhir di simpul yang sama.

Mesh: loop yang tidak mengandung ikatan lain di dalam (mesh penting).

Metode

Analisis mesheal adalah metode umum yang berfungsi untuk memecahkan sirkuit yang elemennya terhubung secara seri, secara paralel atau dicampur, yaitu, ketika jenis koneksi tidak dibedakan dengan jelas. Sirkuit harus datar, atau setidaknya harus dimungkinkan untuk membayarnya seperti itu.

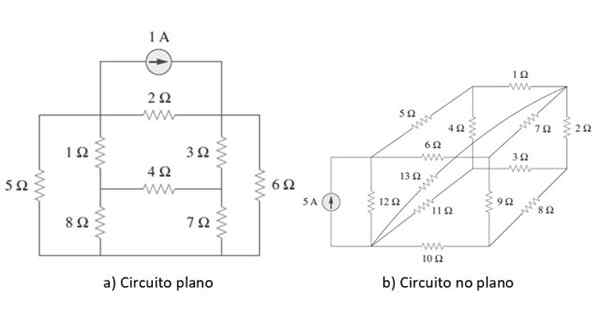Gambar 2. Sirkuit datar dan non -inflat. Sumber: Alexander, C. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.

Contoh setiap jenis sirkuit ditunjukkan pada gambar di atas. Setelah intinya diklarifikasi, untuk memulai, kami akan menerapkan metode ini ke sirkuit sederhana sebagai contoh di bagian selanjutnya, tetapi sebelum kami meninjau secara singkat hukum Ohm dan Kirchhoff.

Hukum Ohm: Sean V Tegangan, R Perlawanan e yo Arus elemen resistif ohmic, di mana tegangan dan arus proporsional secara langsung, resistansi menjadi konstan proporsionalitas:

Dapat melayani Anda: gravitasi API: skala dan klasifikasi minyak mentah

V = i.R

Hukum Tegangan Kirchhoff (LKV): Dalam setiap lintasan tertutup yang ditempuh dalam satu arah, jumlah aljabar dari tegangan adalah nol. Ini termasuk tegangan karena sumber, resistor, induktor atau kapasitor: ∑ e = ∑ r_yo. yo

Kirchhoff dari saat ini (LKC): Dalam simpul apa pun, jumlah aljabar dari arus adalah nol, dengan mempertimbangkan bahwa arus yang masuk diberi tanda dan yang lain keluar. Dengan cara ini: ∑ i = 0.

Dengan metode arus mesh itu tidak perlu.

- Langkah -langkah untuk menerapkan analisis mesh

Kami akan mulai menjelaskan metode untuk sirkuit 2 jerat. Prosedur ini dapat diperpanjang nanti untuk sirkuit yang lebih besar.

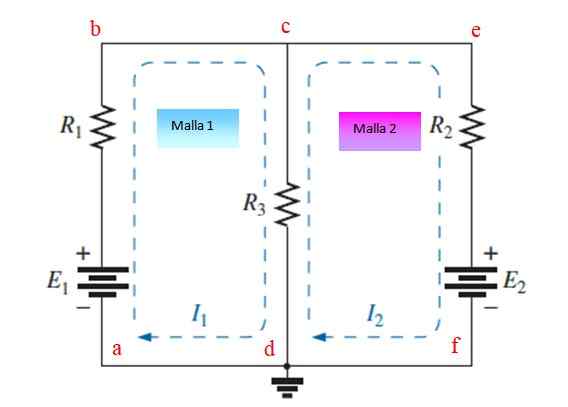Gambar 3. Sirkuit dengan resistensi dan sumber yang disusun dalam dua jerat. Sumber: f. Zapata.

Langkah 1

Menetapkan dan menggambar arus independen ke setiap mesh, dalam contoh ini yo₁ Dan yo₂. Mereka dapat ditarik dalam jadwal atau anti -SHORARY.

Langkah 2

Terapkan Hukum Ketegangan Kirchhoff (LTK) dan Hukum Ohm untuk setiap jala. Potensi jatuh diberi tanda (-) sementara peningkatan ditetapkan tanda (+).

ABCDA MESH

Mulai dari titik A dan mengikuti arti arus, kami menemukan peningkatan potensi dalam baterai E1 (+), kemudian jatuh di R₁ (-) dan kemudian jatuh lagi di R₃ (-).

Secara bersamaan, resistensi r₃ Itu juga dilintasi oleh saya saat ini₂, Tetapi dalam arah yang berlawanan, oleh karena itu merupakan kenaikan (+). Persamaan pertama adalah seperti ini:

DAN₁-R₁.yo₁ -R₃.yo₁ + R₃.yo₂ = 0

Segera memperhitungkan dan mengarahkan kembali istilah:

- (R₁+R₃)YO₁ +R₃yo₂ = -E₁  (Persamaan 1)

Mesh cefdc 

Mulai dari titik Dan dan mengikuti arti arus adalah penurunan potensial R₂ (-), kejatuhan lainnya DAN₂, karena arus masuk melalui tiang baterai + dan akhirnya jatuh lagi R₃ (-), pada saat yang sama saat ini yo₁ Itu melintasi R₃ Di arah yang berlawanan (+).

Persamaan kedua, dengan tanda -tanda yang ditunjukkan, tetap dengan cara ini:

- R₂ yo₂ - DAN₂ -R₃ yo₂ +R₃ yo₁= 0

R₃yo₁ - (R₂ +R₃₎ yo₂ = E₂  (Persamaan 2)

Perhatikan bahwa ada dua persamaan dengan dua yang tidak diketahui dan₁ dan saya₂.

Langkah 3

Maka sistem persamaan yang terbentuk diselesaikan.

Latihan terpecahkan

Untuk memulai, penting untuk mempertimbangkan hal -hal berikut:

-Ikatan atau arus mesh dapat diberi arah sewenang -wenang.

-Untuk setiap mesh penting - atau "jendela" - bahwa sirkuit harus diberi arus.

Dapat melayani Anda: proses isocoric

-Arus mesh dipanggil dengan huruf kapital untuk membedakannya dari arus yang beredar di cabang, meskipun dalam beberapa kasus arus yang beredar melalui cabang dapat sama dengan yang dari mesh.

- Contoh 1

Temukan arus yang beredar melalui setiap resistansi di sirkuit pada Gambar 3, jika elemen memiliki nilai berikut:

R₁ = 20 Ω; R₂ = 30 Ω; R₃ = 10 Ω; DAN₁ = 12 V; DAN₂ = 18 v

Larutan

Pertama -tama perlu untuk menetapkan arus mesh dan₁ dan saya₂ dan ambil sistem persamaan yang disimpulkan di bagian sebelumnya, lalu ganti nilai yang diberikan dalam pernyataan:

- (R₁+R₃)YO₁ +R₃yo₂ = -E₁  (Persamaan 1)

R₃yo₁ - (R₂ +R₃₎ yo₂ = E₂     (Persamaan 2)

-

-(20+30) yo₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-lima puluhyo₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Karena ini adalah sistem persamaan 2 x 2, dapat dengan mudah diselesaikan dengan reduksi, dikalikan dengan 5 persamaan kedua untuk menghilangkan yang tidak diketahui yo₁:

-lima puluhyo₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

yo₂ = - 78/180 a = - 0.41 a

Arus segera dihapus yo₁ dari salah satu persamaan asli:

yo₁ = (18 + 40 i₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Tanda negatif dalam arus yo₂ berarti bahwa arus dalam 2 mesh bersirkulasi bertentangan dengan gambar.

Arus di setiap resistensi adalah sebagai berikut:

Untuk perlawanan R₁ Arus beredar yo₁ = 0.16 a Dalam arti yang ditarik, dengan perlawanan R₂ Arus beredar yo₂ = 0.41 a bertentangan dengan yang ditarik, dan untuk perlawanan R₃ beredar yo₃ = 0.16- (-0.41) a = 0.57 a turun.

Solusi sistem dengan metode Cramer

Dengan cara matriks, sistem dapat diselesaikan sebagai berikut:

Langkah 1: Hitung δ

 Penting: Ketika Δ = 0, sistem tidak memiliki solusi, itu adalah sistem yang tidak kompatibel.

Langkah 2: Hitung δ₁

Kolom pertama digantikan oleh istilah independen dari sistem persamaan, mempertahankan urutan di mana sistem awalnya dinaikkan:

Langkah 3: Hitung i₁

yo₁ = Δ₁/Δ = 300/1900 = 0.16 a

Langkah 4: Hitung δ₂

 Langkah 5: Hitung i₂

yo₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Contoh 2

Tentukan arus dan tegangan melalui setiap resistansi di sirkuit berikut, dengan menggunakan metode arus mesh:

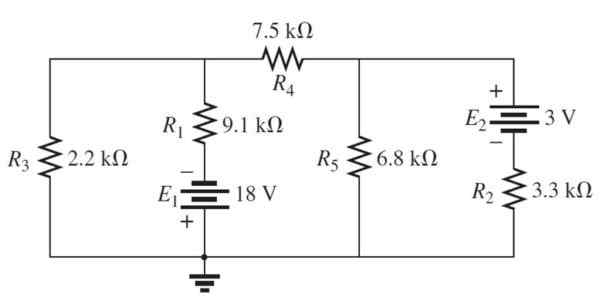Gambar 4. 3 sirkuit mesh. Sumber: Boylestad, R. 2011. Pengantar Analisis Sirkuit.2nd. Edisi. Pearson.

Larutan

Tiga arus mesh ditarik, seperti yang ditunjukkan pada gambar berikut, dalam pengertian sewenang -wenang. Sekarang jerat berjalan dari mana saja:

Itu dapat melayani Anda: imantation: apa yang terdiri dari, metode, dan contoh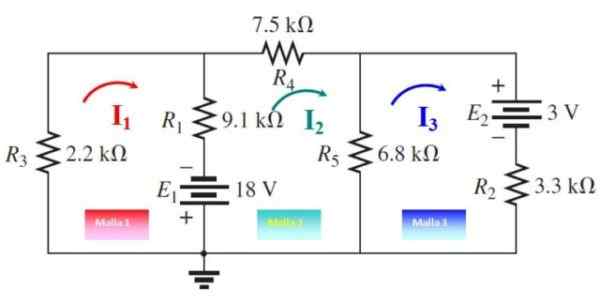 Gambar 5. Arus jala untuk latihan 2. Sumber: f. Zapata, dimodifikasi dari boylestad.

Mesh 1

-9100.yo₁+18-2200.yo₁+9100.yo₂= 0

-11300 i₁ + 9100.yo₂ = -18

Mesh 2       

-(7500 +6800 +9100) .yo₂ + 9100.yo₁+6800.yo₃-18 = 0

9100.yo₁ - 23400.yo₂ + 6800.yo₃ = 18

Mesh 3  

-(6800 + 3300) i₃ + 6800.yo₂ - 3 = 0

6800.yo₂ - 10100.yo₃ = 3

Sistem Persamaan

-11300 i₁ + 9100.yo₂ + 0.yo₃= -18

9100.yo₁ - 23400.yo₂ + 6800.yo₃ = 18

0.yo₁ + 6800.yo₂ - 10100.yo₃ = 3

Meskipun jumlahnya besar, dengan cepat diselesaikan dengan bantuan kalkulator ilmiah. Ingatlah bahwa persamaan harus dipesan dan tambahkan nol di tempat -tempat yang tidak diketahui tidak muncul, seperti yang muncul di sini.

Arus mesh adalah:

yo₁ = 0.0012 a; yo₂ = -0.00048 a; yo₃ = -0.00062 a

Arus yo₂ Dan yo₃ Mereka beredar ke arah yang berlawanan pada gambar, karena mereka ternyata negatif.

Tabel arus dan tegangan di setiap resistensi

Resistensi (Ω)	Saat ini (amp)	Tegangan = i.R (volts)
9100	yo1 -yo2 = 0.0012-(-0.00048) = 0.00168	limabelas.3
3300	0.00062	2.05
2200	0.0012	2.64
7500	0.00048	3.60
6800	yo2 -yo3= -0.00048-(-0.00062) = 0.00014	0.95

Solusi aturan cramer

Karena jumlah besar, lebih mudah menggunakan notasi ilmiah untuk bekerja dengan mereka secara langsung.

Perhitungan i₁

Panah warna dalam penentu 3 x 3 menunjukkan cara menemukan nilai numerik, mengalikan nilai yang ditunjukkan. Mari kita mulai dengan mendapatkan yang dari braket pertama dalam penentu Δ:

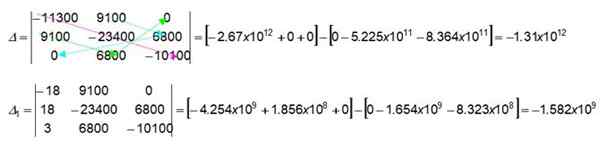
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0

9100 x 6800 x 0 = 0

Kami segera mendapatkan braket kedua dalam penentu yang sama, yang bekerja dari kiri ke kanan (untuk braket ini panah berwarna tidak ditarik dalam gambar). Kami mengundang pembaca untuk memverifikasi:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^sebelas

6800 x 6800 x (-11300) = -5.225 x 10^sebelas

Dengan cara yang sama, pembaca juga dapat memverifikasi nilai untuk penentu Δ₁.

Penting: Antara kedua tanda kurung selalu ada tanda negatif.

Akhirnya arus diperoleh yo₁ melalui yo₁ = Δ₁ / Δ

yo₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

Perhitungan i₂

Prosedur ini dapat diulangi untuk menghitung yo₂, Dalam hal ini, untuk menghitung penentu δ₂ Kolom kedua dari penentu Δ digantikan oleh kolom istilah independen dan nilainya ditemukan, sesuai dengan prosedur yang dijelaskan.

Namun, seperti yang rumit karena jumlah besar, terutama jika tidak ada kalkulator ilmiah, yang paling sederhana adalah menggantikan nilai yo₁ Sudah dihitung, dalam persamaan berikut dan jelas:

-11300 i₁ + 9100.yo₂ + 0.yo₃= -18 → 9100 i₂= -18 + 11300 i₁ → i₂ = -0.00048 a

Perhitungan i3

Sekali dengan nilai -nilai yo₁ Dan yo₂ Di tangan, yo₃ Itu langsung ditemukan dengan substitusi.

Referensi

1. Alexander, c. 2006. Yayasan Sirkuit Listrik. 3. Edisi. MC Graw Hill.
2. Boylestad, r. 2011. Pengantar Analisis Sirkuit.2nd. Edisi. Pearson.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 5. Interaksi listrik. Diedit oleh Douglas Figueroa (USB).
4. Garcia, l. 2014. Elektromagnetisme. 2nd. Edisi. Universitas Industri Santander.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 2.