Rumus dan Persamaan Antiderivatif, Contoh, Latihan

A Antiderivatif F (x) dari suatu fungsi F(x) juga disebut primitif atau hanya integral yang tidak terbatas dari fungsi tersebut, jika dalam interval tertentu yo, Memang benar itu F '(x) = f (x)

Misalnya, mari kita ambil fungsi berikut:

f (x) = 4x³

Antiderivatif dari fungsi ini adalah f (x) = x⁴, karena dengan memperoleh f (x) oleh aturan derivasi untuk kekuatan:

Diperoleh dengan tepat f (x) = 4x³.

Namun, ini hanya salah satu dari banyak antiderivatif f (x), karena fungsi lain ini: g (x) = x⁴ + 2 Juga, karena dengan mendapatkan g (x) sehubungan dengan x, itu sama diperoleh kembali f (x).

Mari kita periksa:

Ingatlah bahwa yang berasal dari konstanta adalah 0. Oleh karena itu untuk istilah x⁴ Anda dapat menambahkan konstanta apa pun dan turunannya akan terus menjadi 4x³.

Disimpulkan bahwa setiap fungsi dari bentuk umum f (x) = x⁴ + C, di mana c adalah konstanta nyata, berfungsi sebagai antiderivatif f (x).

Contoh ilustratif sebelumnya dapat dinyatakan sebagai berikut:

df (x) = 4x³ Dx

Oleh karena itu, antiderivatif atau integral yang tidak terdefinisi diekspresikan dengan simbol ∫, oleh karena itu:

F (x) = ∫4x³ dx = x⁴ + C

Dimana fungsi f (x) = 4x³  Itu disebut mengintegrasikan, dan C adalah Integrasi Konstan.

[TOC]

Contoh Antiderivatif

Gambar 1. Anti -hotley tidak lebih dari integral yang tidak terbatas. Sumber: Pixabay.

Menemukan antiderivatif suatu fungsi sederhana dalam beberapa kasus di mana turunannya sudah diketahui. Sebagai contoh, jadilah fungsi f (x) = sen x, yang tidak diiderivasi untuk itu adalah fungsi lain f (x), sehingga ketika diturunkan diperoleh f (x).

Fungsi itu bisa:

F (x) = - cos x

Mari kita periksa apakah itu benar:

F '(x) = (- cos x)' =- (-sen x) = sin x

Oleh karena itu kita bisa menulis:

∫Sen x dx = -cos x + c

Selain mengetahui turunannya, ada aturan integrasi dasar dan sederhana untuk menemukan antiderivatif atau integral yang tidak terbatas.

Dapat melayani Anda: turunan berturut -turut

Jadilah konstanta yang nyata, kalau begitu:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Jika fungsi H (x) dapat dinyatakan sebagai jumlah atau pengurangan dua fungsi, maka integral yang tidak terbatas adalah:

3.- ∫H (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Ini adalah sifat linearitas.

Itu Aturan kekuasaan Untuk integral dapat ditetapkan dengan cara ini:

Aturan ini memiliki batasan yang jelas: karena penyebutnya N +1 Itu tidak dapat dilakukan 0, oleh karena itu n ≠ -1.

Dalam kasus n = -1 aturan berikut digunakan:

5.- ∫X ^-1 Dx = ln x +c

Mudah untuk menunjukkan bahwa turunannya ln x itu justru X ^-1.

Persamaan diferensial

Persamaan diferensial adalah satu di mana yang tidak diketahui adalah sebagai turunan.

Sekarang, dari analisis sebelumnya, mudah untuk menyadari bahwa operasi terbalik ke turunannya adalah antiderivatif atau integral yang tidak ditentukan.

Biarkan f (x) = y '(x), yaitu, berasal dari fungsi tertentu. Kita dapat menggunakan notasi berikut untuk menunjukkan turunan ini:

Segera mengikutinya:

dy = f (x) dx

Yang tidak diketahui dari persamaan diferensial adalah fungsi y (x), yang turunannya adalah f (x). Untuk membersihkannya, ekspresi sebelumnya terintegrasi di kedua sisi, yang setara dengan menerapkan antiderivatif:

∫dy = ∫f (x) dx

Integral kiri diselesaikan dengan aturan integrasi 1, dengan k = 1 dan dengan demikian dicari -Awaite dibersihkan:

dan (x) = ∫f (x) dx = f (x) + c

Dan karena C adalah konstanta nyata, untuk mengetahui mana yang sesuai dalam setiap kasus, pernyataan tersebut harus berisi informasi tambahan yang cukup untuk menghitung nilai C. Ini disebut Kondisi awal.

Kita akan melihat contoh penerapan semua ini di bagian selanjutnya.

Dapat melayani Anda: perkiraan waktu

Latihan yang antiderivasi

- Latihan 1

Menerapkan aturan integrasi untuk mendapatkan antiderivatif yang tidak ditentukan berikut atau integral dari fungsi yang diberikan, menyederhanakan hasil sebanyak mungkin. Lebih mudah untuk memverifikasi hasilnya dengan derivasi.

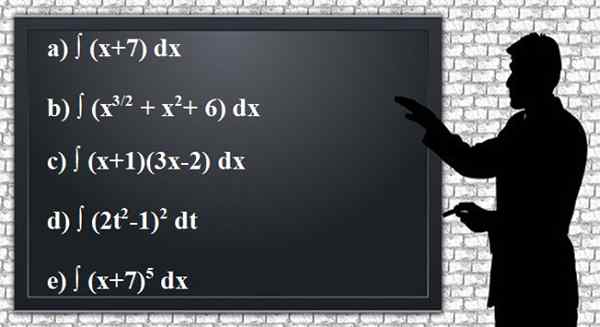Gambar 2. Latihan yang di -anterivasi atau integral didefinisikan. Sumber: Pixabay.

Solusi untuk

Kami pertama -tama menerapkan aturan 3, karena integrasi adalah jumlah dari dua istilah:

∫ (x +7) dx = ∫ xdx +∫7dx

Untuk integral pertama, aturan kekuatan diterapkan:

∫ xdx = (x² /2)+C₁

Dalam aturan integral kedua 1 berlaku, menjadi k = 7:

∫7dx = 7∫dx = 7x + c₂

Dan sekarang hasilnya ditambahkan. Dua konstanta dikelompokkan menjadi satu, secara umum disebut C:

∫ (x+7) dx = (x² /2) + 7x + c

Solusi b

Dengan linearitas ini terurai integral menjadi tiga integral yang lebih sederhana, di mana aturan kekuasaan akan diterapkan:

∫ (x^3/2 + X² + 6) dx = ∫x^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Perhatikan bahwa untuk setiap integral konstanta integrasi muncul, tetapi mereka bertemu dalam satu panggilan c.

Solusi c

Dalam hal ini, lebih mudah untuk menerapkan properti distributif dari perkalian untuk mengembangkan integrasi. Kemudian Anda menggunakan aturan kekuatan untuk menemukan setiap integral secara terpisah, seperti pada tahun sebelumnya.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Pembaca yang penuh perhatian akan mengamati bahwa kedua istilah pusatnya serupa, oleh karena itu mereka dikurangi sebelum berintegrasi:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Solusi e

Cara untuk menyelesaikan integral adalah dengan mengembangkan kekuatan, seperti yang dilakukan pada contoh d. Namun, karena eksponen lebih tinggi, perlu untuk membuat perubahan variabel, sehingga tidak harus membuat pengembangan yang begitu lama.

Dapat melayani Anda: variabel acak kontinu

Perubahan variabel adalah sebagai berikut:

U = x + 7

Turun di kedua sisi ekspresi ini:

du = dx

Integral diubah menjadi lebih sederhana dengan variabel baru, yang diselesaikan dengan aturan kekuatan:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Akhirnya, perubahan dikembalikan untuk kembali ke variabel asli:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Latihan 2

Partikel awalnya beristirahat dan bergerak di sepanjang sumbu x. Percepatannya untuk t> 0 diberikan oleh fungsi a (t) = cos t. Diketahui bahwa pada t = 0, posisinya adalah x = 3, semuanya dalam satuan sistem internasional. Itu diminta untuk menemukan kecepatan v (t) dan posisi x (t) dari partikel.

Larutan

Karena akselerasi adalah yang pertama berasal dari kecepatan sehubungan dengan waktu, Anda memiliki persamaan diferensial berikut:

a (t) = v '(t) = cos t

Itu mengikuti itu:

v (t) = ∫ cos t dt = sin t + c₁

Di sisi lain, kita tahu bahwa kecepatan pada gilirannya turunan dari posisi, oleh karena itu kita berintegrasi lagi:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Konstanta integrasi ditentukan dari informasi yang diberikan dalam pernyataan tersebut. Pertama, ia mengatakan bahwa partikel itu awalnya sedang istirahat, oleh karena itu V (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Maka Anda harus x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → c₂ = 3+1 = 4

Fungsi kecepatan dan posisi pasti seperti ini:

v (t) = sen t

x (t) = - cos t + 4

Referensi

1. Engler, a. 2019. Kalkulus integral. Universitas Nasional Pantai.
2. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
3. Teks Matematika Gratis. Antiderivatif. Pulih dari: matematika.Liibretexts.org.
4. Wikipedia. Antiderivatif. Diperoleh dari: di.Wikipedia.org.
5. Wikipedia. Integrasi yang tidak terbatas. Pulih dari: is.Wikipedia.org.