Definisi, rumus, dan latihan rig faktorial

Dia Rig faktorial Ini adalah mesin sederhana yang terdiri dari pengaturan katrol dengan efek penggandaan kekuatan. Dengan cara ini Anda dapat menaikkan beban yang menerapkan setara dengan sebagian kecil dari berat di ujung tali bebas.

Ini terdiri dari dua set katrol: satu yang ditetapkan untuk dukungan dan lainnya yang memberikan gaya yang dihasilkan pada beban. Katrol dipasang pada bingkai logam yang umumnya menahannya. 

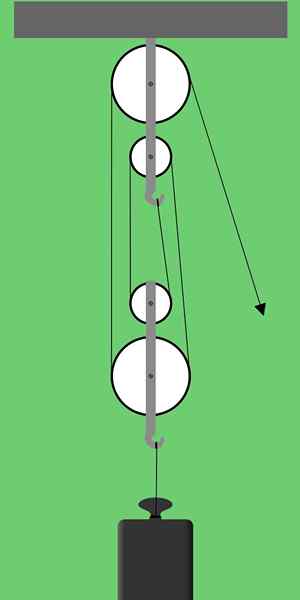
Gambar 1. Skema rig faktorial. Sumber: Pixabay

Gambar 1 menunjukkan rig faktorial yang masing -masing terdiri dari dua kelompok dua katrol. Jenis pengaturan katrol ini juga disebut Rig seri salah satu Polipast.

[TOC]

Formula kanan faktorial

Kasus 1: Katrol seluler dan tetap

Untuk memahami mengapa pengaturan ini melipatgandakan gaya yang diberikan, kita akan mulai dengan kasus paling sederhana, yang terdiri dari katrol tetap dan seluler.

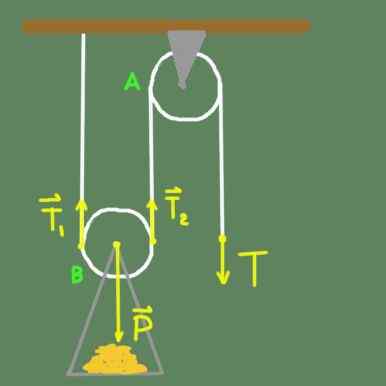Gambar 2. Dua rig katrol.

Pada Gambar 2 kami memiliki katrol tetap ke atap dengan dukungan. Katrol A dapat berputar dengan bebas di sekitar porosnya. Kami juga memiliki katrol B yang memiliki dukungan tetap pada sumbu katrol, di mana beban ditempatkan. Pulley B, selain bisa berputar bebas di sekitar porosnya, memiliki kemungkinan untuk bergerak secara vertikal.

Misalkan kita berada dalam situasi keseimbangan. Pertimbangkan kekuatan yang bertindak pada katrol B. Sumbu B -Pulley mendukung berat total P yang diarahkan ke bawah. Jika ini adalah satu -satunya kekuatan pada katrol B maka, tetapi kita tahu bahwa tali yang melewati katrol ini juga memberikan dua kekuatan, yang merupakan T1 dan T2 yang diarahkan ke atas.

Agar keseimbangan translasi, kedua kekuatannya harus sama dengan berat yang mendukung poros katrol B.

T1 + t2 = p

Tetapi karena katrol b juga dalam keseimbangan rotasi, maka t1 = t2. Kekuatan T1 dan T2 berasal dari ketegangan yang diterapkan pada tali, disebut t.

Itu bisa melayani Anda: model atom bohr

Oleh karena itu t1 = t2 = t. Mengganti persamaan sebelumnya tetap:

T + t = p

2t = p

Menunjukkan bahwa ketegangan yang diterapkan pada tali hanya setengah berat:

T = p/2

Misalnya, jika beban 100 kg akan cukup untuk menerapkan gaya 50 kg di ujung bebas tali untuk menaikkan beban pada kecepatan konstan.

Kasus 2: Dua Buku Seluler dan Dua Patrol Tetap

Mari kita pertimbangkan ketegangan dan kekuatan yang bertindak pada set yang terdiri dari dua dukungan dukungan A dan B dengan dua katrol masing -masing.

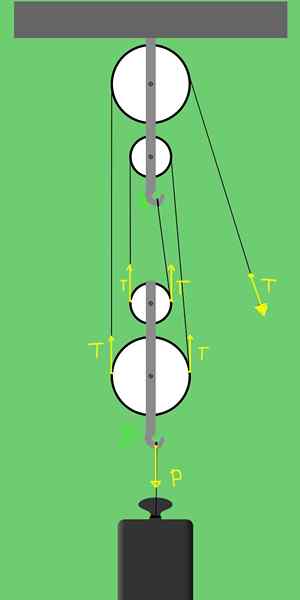Gambar 3. Gaya pada rig 2 katrol tetap dan 2 katrol seluler.

Dukungan B memiliki kemungkinan bergerak secara vertikal, dan kekuatan yang bertindak pada putra:

- Berat p beban, yang menunjuk ke bawah secara vertikal.

- Dua ketegangan pada katrol besar dan dua ketegangan pada katrol kecil. Secara total, empat ketegangan, semuanya menunjuk.

Agar ada keseimbangan translasi, perlu bahwa kekuatan yang menunjuk secara vertikal ke atas sama dengan beban yang menunjuk ke bawah. Yaitu, harus dipenuhi:

T + t + t + t = p

Yaitu, 4 t = p

Dari mana ia mengikuti bahwa gaya T yang diterapkan di ujung tali bebas hanya seperempat dari berat karena beban yang ingin naik., T = p / 4.

Dengan nilai ini untuk tegangan T, beban dapat dipertahankan statis atau naik dengan kecepatan konstan. Jika tegangan yang lebih besar diterapkan dari nilai ini maka beban akan meningkat, kondisi yang diperlukan untuk menghapusnya dari yang lain.

Kasus Umum: n Pulroly Mobile dan N Patroly Tetap

Seperti yang terlihat dalam kasus -kasus sebelumnya, untuk setiap katrol dari set seluler ada beberapa kekuatan ke atas oleh tali yang melewati katrol. Tetapi kekuatan ini tidak bisa apa pun selain ketegangan yang diterapkan pada tali di ujung bebas.

Jadi untuk setiap katrol set seluler akan ada kekuatan ke atas yang bernilai 2t. Tetapi karena ada n katrol di set seluler, maka perlu untuk menunjukkan secara vertikal ke atas adalah:

Dapat melayani Anda: mesin sangkar tupai

2 n t

Untuk keseimbangan vertikal, perlu bahwa:

2 n t = p

Oleh karena itu gaya yang diterapkan di ujung bebas adalah:

T = p / (2 n)

Dalam hal ini dapat dikatakan bahwa gaya yang diberikan T berlipat ganda 2 N kali pada beban.

Misalnya, jika kami memiliki rig faktorial dengan 3 katrol tetap dan 3 ponsel, angka n akan sama dengan 3. Di sisi lain, jika bebannya adalah p = 120 kg, maka gaya yang diterapkan pada ujung bebas akan menjadi t = 120 kg / (2*3) = 20 kg.

Latihan terpecahkan

Latihan 1

Pertimbangkan rig faktorial yang terdiri dari dua katrol tetap dan dua katrol seluler. Ketegangan maksimum yang dapat mendukung tali adalah 60 kg. Tentukan berapa beban maksimum yang dapat ditempatkan.

Larutan

Ketika beban sedang istirahat atau bergerak terus -menerus, beratnya, itu terkait dengan ketegangan t yang diterapkan pada tali melalui hubungan berikut:

P = 2 n t

Karena ini adalah rig dua seluler dan dua katrol tetap, maka n = 2.

Beban maksimum yang dapat ditempatkan diperoleh ketika t memiliki nilai maksimum yang mungkin, yang dalam hal ini adalah 60 kg.

Beban maksimum = 2*2*60 kg = 240 kg

Latihan 2

Temukan hubungan antara ketegangan tali dan berat beban, dalam rig faktorial dua katrol di mana beban berakselerasi dengan akselerasi.

Larutan

Perbedaan dalam contoh ini sehubungan dengan apa yang telah dilihat sejauh ini adalah bahwa dinamika sistem harus dipertimbangkan. Jadi kami mengusulkan undang -undang kedua Newton untuk menemukan hubungan yang diminta.

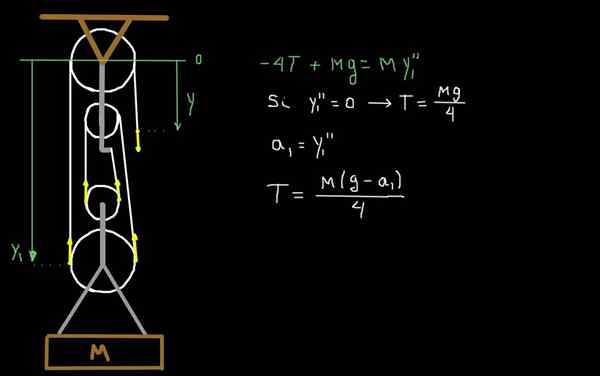Gambar 4. Dinamika rig faktorial.

Pada Gambar 4 kita menarik kekuatan karena ketegangan t tali. Bagian seluler rig memiliki massa total m. Kami mengambil sebagai sistem referensi satu pada tingkat katrol yang tetap dan positif pertama.

Y1 adalah posisi sumbu katrol terendah.

Kami menerapkan undang -undang kedua Newton untuk menentukan percepatan A1 dari bagian seluler rig:

Dapat melayani Anda: Teorema Varignon

-4 t + mg = m a1

Karena berat beban adalah p = mg, di mana g adalah percepatan gravitasi, hubungan sebelumnya dapat ditulis:

-4t + p = p (a1 / g)

Jika kami ingin menentukan ketegangan yang diterapkan pada tali ketika beban berat tertentu dipercepat dengan akselerasi A1, maka hubungan sebelumnya akan seperti ini:

T = p (1 - a1 / g) / 4

Perhatikan bahwa jika sistem sedang istirahat atau bergerak terus -menerus, maka A1 = 0, dan kami memulihkan ekspresi yang sama yang kami peroleh dalam kasus 2.

Latihan 3

Dalam contoh ini rig Latihan 1 yang sama digunakan, dengan tali yang sama yang mendukung maksimum 60 kg ketegangan. Beban tertentu naik, mempercepatnya dari istirahat menjadi 1 m/s dengan 0,5 detik, menggunakan ketegangan maksimum tali. Temukan berat beban maksimum.

Larutan

Kami akan menggunakan ekspresi yang diperoleh dalam Latihan 2 dan sistem referensi pada Gambar 4 di mana alamat positifnya vertikal.

Akselerasi beban adalah A1 = (-1 m/s -0 m/s) /0.5 s = -2 m/s^2.

Berat beban dalam kilogram-kekuatan diberikan oleh

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Ini adalah berat maksimum beban yang mungkin tanpa tali yang rusak. Perhatikan bahwa nilai yang diperoleh kurang dari yang diperoleh dalam Contoh 1, di mana beban dianggap dengan akselerasi nol, yaitu, pada kecepatan istirahat atau konstan.

Referensi

1. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1. 101-120.
2. Resnick, r. (1999). Fisik. Vol. 1. 3 ra ed. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V. 87-103.
3. Giancoli, d. 2006. Fisika: Prinsip dengan aplikasi. 6. Ed. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Ilmu Fisik Konseptual. Ke -5. Ed. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage. 100 - 119.