Ukuran busur (geometri), jenis lengkungan, contoh

Dia busur, Dalam geometri, itu adalah garis melengkung yang menghubungkan dua titik. Garis melengkung, tidak seperti garis lurus, adalah bahwa arahnya berbeda pada setiap titik yang sama. Kebalikan dari busur adalah segmen, karena ini adalah bagian lurus yang bergabung dengan dua poin.

Busur yang paling sering digunakan dalam geometri adalah busur keliling. Lengkungan penggunaan umum lainnya adalah lengkungan parabola, lengkungan elips dan lengkungan catenary. Bentuk busur juga sering digunakan dalam arsitektur sebagai elemen dekoratif dan elemen struktural. Ini adalah kasus ambang pintu dan jendela, serta dari jembatan dan saluran air.

Gambar 1. The Rainbow adalah garis melengkung yang bergabung dengan dua titik di cakrawala. Sumber: Pixabay

[TOC]

Busur dan ukurannya

Ukuran busur adalah panjangnya, yang tergantung pada jenis kurva yang menghubungkan kedua titik dan lokasi mereka.

Panjang busur melingkar adalah salah satu yang paling mudah dihitung, karena panjang busur penuh atau perimeter lingkaran diketahui.

Perimeter lingkaran adalah dua pi kali radio Anda: P = 2 π r. Mengetahui hal ini, jika Anda ingin menghitung panjangnya S dari lengkungan sudut lingkaran α (diukur dalam radianes) dan radio R, Proporsi diterapkan:

(s / p) = (α / 2 π)

Lalu membersihkan S dari ekspresi sebelumnya dan mengganti perimeter P dengan ekspresinya tergantung pada radio R, Kamu punya:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α R.

Yaitu, ukuran busur melingkar adalah produk dari bukaan sudutnya oleh jari -jari busur melingkar.

Untuk busur secara umum masalahnya lebih rumit, sampai -sampai para pemikir hebat kuno mengklaim bahwa itu adalah tugas yang mustahil.

Itu dapat melayani Anda: apa itu ekspresi aljabar dan mana yang paling sering?

Tidak sampai munculnya kalkulus diferensial dan integral pada tahun 1665, masalah ukuran busur apa pun diselesaikan dengan memuaskan. 

Sebelum penemuan kalkulus diferensial, hanya solusi yang dapat ditemukan melalui penggunaan garis poligonal atau lengkungan keliling yang mendekati lengkungan sejati, tetapi solusi ini tidak tepat. 

Jenis lengkungan

Dari sudut pandang geometri, lengkungan diklasifikasikan menurut garis melengkung yang bergabung dengan dua titik pesawat. Ada klasifikasi lain sesuai dengan penggunaan dan bentuk arsitekturnya.

Busur melingkar

Saat garis yang menghubungkan dua titik pesawat adalah sepotong lingkar jari -jari tertentu, ada busur melingkar. Gambar 2 menunjukkan busur lingkaran jari -jari R yang menghubungkan titik A dan B.

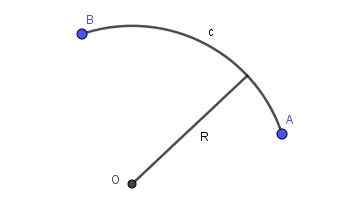Gambar 2. Radio R Circular Arc yang menghubungkan titik A dan B. Disiapkan oleh Ricardo Pérez.

Arc Parabolic

Perumpamaan adalah lintasan yang mengikuti objek yang telah dilemparkan ke udara dalam bentuk miring. Ketika kurva yang bergabung dengan dua titik adalah perumpamaan, maka ada lengkungan parabola seperti yang ditunjukkan pada Gambar 3.

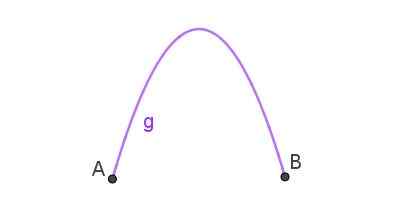Gambar 3. Busur parabola yang menghubungkan titik A dan B. Disiapkan oleh Ricardo Pérez.

Ini adalah bentuk yang mengadopsi jet air yang keluar dari selang yang menunjuk. Lengkungan parabola dapat diamati di sumber air.

Gambar 4. Busur parabola dibentuk oleh air dari sumber di Dresden. Sumber: Pixabay.

Catenary Arc

Busur catenary adalah lengkungan alami lainnya. Catenary adalah kurva yang secara alami terbentuk ketika rantai atau tali digantung dengan nyaman dari dua titik terpisah.

Dapat melayani Anda: apa elemen sudut?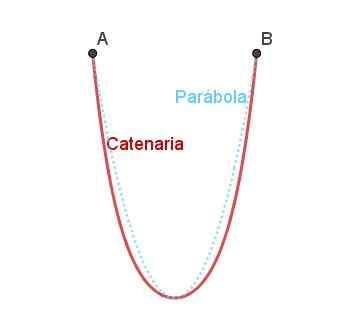 Gambar 5. Busur catenary dan perbandingan dengan lengkungan parabola. Disiapkan oleh Ricardo Pérez.

Catenary mirip dengan parabola, tetapi tidak persis sama seperti yang dapat dicatat pada Gambar 4.

Lengkungan berbentuk catenary terbalik digunakan dalam arsitektur sebagai elemen struktural dari resistensi kompresi tinggi. Faktanya, dapat ditunjukkan bahwa itu adalah tipe busur yang paling resisten di antara semua bentuk yang mungkin. 

Untuk membangun busur catenary yang kokoh, hanya bentuk tali atau rantai yang disalin, kemudian bentuk yang disalin berubah untuk mereproduksi di pintu atau jendela pintu.

Busur elips

Busur bersifat elips jika kurva yang menghubungkan dua titik adalah peregangan atau bentangan elips. Elips didefinisikan sebagai tempat geometris dari titik -titik yang jaraknya ke dua titik yang diberikan selalu menambah jumlah konstan.

Elips adalah kurva yang muncul di alam: itu adalah kurva lintasan planet di sekitar matahari, seperti yang ditunjukkan Johannes Kepler pada 1609.

Dalam praktiknya, elips dapat ditarik dengan mengatur dua struts di lantai atau dua pin di atas kertas dan mengikat tali kepada mereka. Maka tali tegang dengan penanda atau pensil dan kurva ditarik. Sepotong elips adalah lengkungan elips. Animasi berikut menggambarkan bagaimana elips ditarik:

Gambar 5. Posen elips menggunakan tali tegang. Sumber: Wikimedia Commons

Gambar 6 menunjukkan busur elips yang menghubungkan titik G dan H.

Gambar 6. Busur elips yang menghubungkan dua titik. Disiapkan oleh Ricardo Pérez.

Contoh lengkungan

Contoh -contoh berikut merujuk pada cara menghitung perimeter beberapa lengkungan spesifik.

Dapat melayani Anda: Angka transenden: Apa itu, formula, contoh, latihan

Contoh 1

Gambar 7 menunjukkan jendela yang diakhiri dengan busur melingkar yang dipotong. Dimensi yang ditunjukkan pada gambar berada di atas kaki. Hitung panjang busur.

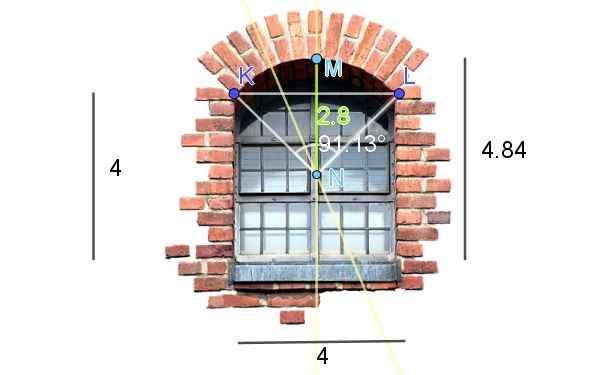Gambar 7. Perhitungan panjang busur melingkar dari sebuah jendela. (Penjelasan Sendiri - Gambar Jendela di Pixabay)

Untuk mendapatkan pusat dan jari -jari busur melingkar dari ambang jendela, konstruksi berikut dibuat pada gambar:

-Segmen KL ditarik dan mediatrixnya ditarik.

-Kemudian titik tertinggi dari ambang pintu berada, yang kami sebut m. Segmen km kemudian dipertimbangkan dan mediatrixnya ditarik.

Intersepsi dua mediatrices adalah titik N dan juga merupakan pusat busur melingkar.

-Sekarang Anda harus mengukur panjang segmen NM, yang bertepatan dengan jari -jari R busur melingkar: r = 2.8 kaki.

-Untuk mengetahui panjang busur selain jari -jari, sudut yang membentuk busur. Yang dapat ditentukan dengan dua metode, atau diukur dengan transporter, atau dihitung secara bergantian menggunakan trigonometri.

Dalam kasus yang ditunjukkan sudut yang membentuk busur adalah 91,13º, yang harus dikonversi menjadi radianes:

 91,13º = 91,13º * π / 180º = 1,59 radian

Kami akhirnya menghitung panjangnya S dari busur melalui formula S = α r.

S = 1,59 * 2.8 kaki = 4,45 kaki

Contoh 2

Temukan panjang busur elips yang ditunjukkan pada Gambar 8, diketahui R dan semi -axis minor S elips.

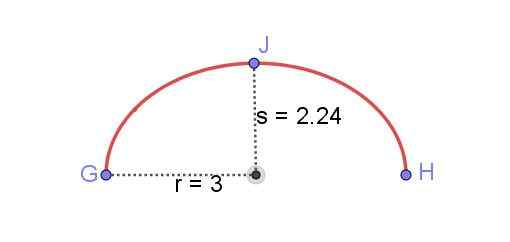Angka 8. Busur elips antara GH. Disiapkan oleh Ricardo Pérez.

Menemukan panjang elips adalah untuk waktu yang lama salah satu masalah matematika yang paling sulit. Solusi yang diungkapkan oleh integral elips dapat diperoleh tetapi untuk memiliki nilai numerik, integral dalam seri daya ini harus diperluas. Hasil yang tepat akan membutuhkan istilah tak terbatas dari seri tersebut.

Untungnya, kejeniusan matematika asal Hindu Ramanujan, yang hidup antara tahun 1887 dan 1920, menemukan formula yang mendekati dengan sangat tepat perimeter elips:

Perimeter elips = π [3 (r + s) - √ ((3r + s) (r + 3s))]]

Perimeter elips dengan r = 3 cm dan s = 2.24 cm adalah 16,55 cm. Namun, lengkungan elips yang ditampilkan memiliki setengah dari nilai itu:

Panjang busur elips gh = 8.28 cm.

Referensi

1. Clemens s. 2008. Geometri dan Trigonometri. Pendidikan Pearson.
2. Garcia f. Prosedur Numerik di Java. Panjang elips. Diperoleh dari: sc.Ehu.adalah
3. Geometri dinamis. Lengkungan. Pulih dari geometriadinamica.adalah
4. PIZEDAS. Elips dan perumpamaan di sekitar kita. Diperoleh dari: pizateas.com
5. Wikipedia. Busur (geometri). Pulih dari: itu.Wikipedia.com