Sifat dasar, contoh dan latihan Ortonormal

A Basis Ortonormal Ini dibentuk dengan vektor tegak lurus satu sama lain dan yang modulnya juga bernilai 1 (unit vektor). Ingatlah itu basis B di ruang vektor V, Itu didefinisikan sebagai satu set vektor independen linier yang mampu menghasilkan ruang ini.

Pada gilirannya, ruang vektor adalah entitas matematika abstrak antara unsur -unsurnya yang vektor, umumnya terkait dengan besaran fisik seperti kecepatan, kekuatan dan perpindahan atau juga matriks, polinomial dan fungsi.

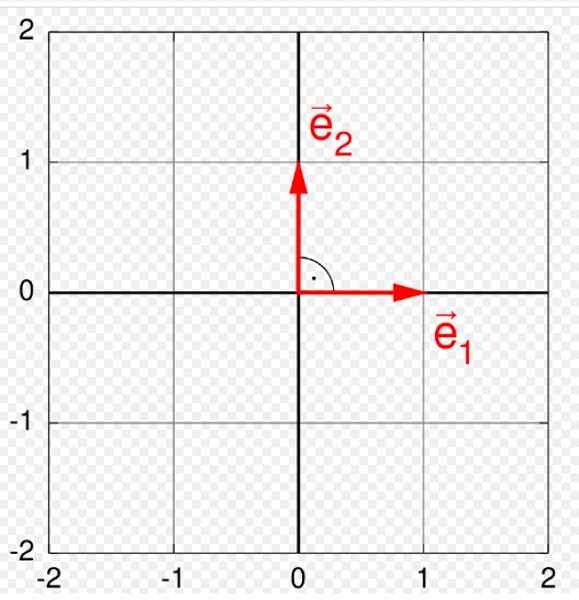
Gambar 1. Dasar ortonormal di pesawat. Sumber: Wikimedia Commons. Quartl [CC BY-SA (https: // CreationCommons.Org/lisensi/by-sa/3.0)].

Vektor memiliki tiga elemen khas: besarnya atau modul, arah dan makna. Basis ortonormal sangat berguna untuk mewakili dan beroperasi dengan mereka, karena vektor apa pun yang termasuk ruang vektor tertentu V, Itu dapat ditulis sebagai kombinasi linier dari vektor yang membentuk basis ortonormal.

Dengan cara ini, operasi antara vektor, seperti jumlah, pengurangan dan berbagai jenis produk yang didefinisikan dalam ruang tersebut dianalisis secara analitik.

Di antara basis fisika yang paling banyak digunakan adalah basis yang dibentuk oleh vektor unit yo, J Dan k mewakili tiga arah khas ruang tiga dimensi: tinggi, lebar dan kedalaman. Vektor -vektor ini juga dikenal dengan nama Vektor kanonik kesatuan.

Jika, sebaliknya, vektor bekerja di pesawat, itu akan cukup dengan dua dari tiga komponen ini, sementara hanya satu.

[TOC]

Properti Basis

1- Basis B Ini adalah set vektor sekecil mungkin yang menghasilkan ruang vektor V.

2- elemen dari B Mereka mandiri secara linear.

3- Basis apa pun B ruang vektor V, memungkinkan untuk mengekspresikan semua vektor V Sebagai kombinasi linier dan bentuk ini unik untuk setiap vektor. Oleh karena itu a B Itu juga dikenal sebagai Sistem Generator.

4- Ruang vektor yang sama V dapat memiliki pangkalan yang berbeda.

Dapat melayani Anda: gaya sentrifugal: formula, bagaimana itu dihitung, contoh, latihan

Contoh pangkalan

Di bawah beberapa contoh basis dan pangkalan ortonormal secara umum:

Basis kanonik di ℜ ^N

Juga disebut basis alami atau basis standar ℜ ^N, Dimana ℜ ^N Itu ruang n-dimensi, Misalnya, ruang tiga -dimensi adalah ℜ ³. Ke nilai N Itu disebut dimensi ruang vektor dan menunjukkan sebagai Redup (v).

Semua vektor milik ℜ ^N Mereka diwakili oleh N-USA Dipesan. Untuk ruang ℜ^N, Basis kanonik adalah:

Dan₁ =; Dan₂ =; Dan_N =

Dalam contoh ini kami telah menggunakan notasi dengan tanda kurung atau "kurung" dan berani untuk vektor unit Dan₁, Dan₂, Dan₃..

Basis kanonik di ℜ³

Vektor keluarga yo, J Dan k Mereka mengakui representasi yang sama ini dan mereka cukup untuk tiga untuk mewakili vektor di ℜ ³:

yo =; J =;  k =

Itu berarti bahwa basis dapat dinyatakan sebagai berikut:

B = ; ;

Untuk memverifikasi bahwa mereka secara linear independen, penentu yang dibentuk dengan mereka vektor adalah non -null dan juga sama dengan 1:

Juga harus dimungkinkan untuk menulis vektor apa pun yang dimiliki ℜ ³ Sebagai kombinasi linier dari mereka. Misalnya, gaya yang komponen persegi panjangnya adalah f_X = 4 n, f_Dan = -7 n dan f_z= 0 n akan ditulis dalam bentuk vektor sebagai berikut:

F = N = 4yo -7J + 0k N.

Karena itu yo, J Dan k membuat sistem generator ℜ ³.

Basis ortormal lainnya di ℜ³

Basis standar yang dijelaskan pada bagian sebelumnya bukan satu -satunya basis ortonormal di ℜ³. Di sini kita memiliki contohnya:

B₁ = ; ;

B₂ = ; ;

Dapat ditunjukkan bahwa basis ini ortonormal, karena ini kita ingat kondisi yang harus dipenuhi:

Dapat melayani Anda: optik bergelombang

-Vektor yang membentuk basis harus ortogonal satu sama lain.

-Masing -masing harus kesatuan.

Kita dapat memverifikasi bahwa mengetahui bahwa penentu yang dibentuk oleh mereka harus bukan -null dan sama dengan 1.

Basis b₁ Justru koordinat silinder ρ, φ dan z, cara lain untuk mengekspresikan vektor di luar angkasa.

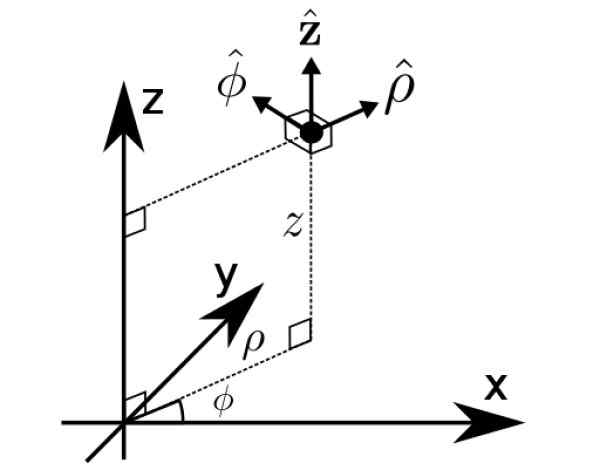Gambar 2. Koordinat silinder. Sumber: Wikimedia Commons. Buff matematika [CC BYS-S (https: // createveCommons.Org/lisensi/by-sa/4.0)].

Latihan terpecahkan

- Latihan 1

Tunjukkan bahwa basis b = ; ; ortonormal.

Larutan

Untuk menunjukkan bahwa vektor saling tegak lurus, kami akan menggunakan produk skalar, juga disebut titik internal atau produk dari dua vektor.

Biarkan dua vektor atau Dan v, Produk skalar Anda ditentukan oleh:

atau • v = atau.v. cosθ

Untuk membedakan vektor dari modul mereka, kami akan menggunakan huruf tebal untuk huruf pertama dan normal untuk yang terakhir. θ adalah sudut antara atau Dan v, Oleh karena itu jika mereka tegak lurus, itu berarti θ = 90º dan produk skalar batal.

Atau, jika vektor diberikan dalam hal komponen mereka: atau = X, atau_Dan,atau_z > dan v = X, v_Dan,v_z >, produk skalar keduanya, yang komutatif, dihitung dengan cara ini:

atau • v = atau_X .v_X + atau_Dan .v_Dan + atau_z .v_z

Dengan cara ini, produk skalar antara masing -masing pasangan vektor masing -masing:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Untuk kondisi kedua, modul masing -masing vektor dihitung, yang diperoleh oleh:

│U │ = √ (u_X² + atau_Dan² + atau_z²)

Dengan demikian, modul masing -masing vektor adalah:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Itu dapat melayani Anda: Kondisi keseimbangan kedua: penjelasan, contoh, latihan

│ = √ [0² + 0²  + 1²)] = 1

Oleh karena itu ketiganya adalah vektor unit. Akhirnya, penentu bentuknya tidak nol dan sama dengan 1:

- Latihan 2

Tulis koordinat vektor W = Dalam hal basis sebelumnya.

Larutan

Untuk melakukannya, teorema berikut digunakan:

Biarkan b = v₁, v₂, v₃,.. v_N Basis ortonormal di ruang V dengan produk domestik, vektor W Itu diwakili oleh B sebagai berikut:

W = <W•v₁> v₁ + <W•v₂> v₂ +<W•v₃> v₃ +.. <W•v_N> v_N

Ini berarti bahwa kita dapat menulis vektor di base B, melalui koefisien <W•v₁>, <W•v₂>, ..  <W•v_N>, untuk itu Anda harus menghitung skalar yang ditunjukkan:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Dengan produk skalar yang diperoleh, matriks dibangun, disebut Koordinat matriks dari w.

Oleh karena itu koordinat vektor W Di pangkalan B mereka diekspresikan melalui:

[W]_B= [(18/5); (1/5); 1]

Matriks koordinat bukan vektor, karena vektor tidak sama dengan koordinatnya. Ini hanya satu set angka yang berfungsi untuk mengekspresikan vektor pada basis yang diberikan, bukan vektor seperti itu. Mereka juga bergantung pada basis yang dipilih.

Akhirnya, mengikuti teorema, vektor W akan dinyatakan sebagai berikut:

W = (18/5) v₁ + (1/5) v₂ + v₃

Dengan: v₁ =; v₂ =; v₃ =, Yaitu vektor dasar B.

Referensi

1. Larson, r. Dasar -dasar aljabar linier. 6. Edisi. Pembelajaran Cengage.
2. Larson, r. 2006. Perhitungan. 7. Edisi. Volume 2. Bukit McGraw.
3. Salas, J. aljabar linier. Topik 10. Basis Ortonormal. Pulih dari: ocw.UC3M.adalah.
4. Universitas Sevilla. Koordinat silindris. Basis vektor. Pulih dari: Laplace.kita.adalah.
5. Wikipedia. Basis Ortonormal. Pulih dari: is.Wikipedia.org.