Binomial terkonjugasi bagaimana diselesaikan, contoh, latihan

A Binomial terkonjugasi Dari binomial lain adalah salah satu di mana mereka hanya berbeda dengan tanda operasi. Binomial, sesuai namanya, adalah struktur aljabar yang terdiri dari dua istilah.

Beberapa contoh binomial adalah: (A + B), (3m - n) Dan (5x - y). Dan binomial terkonjugasi masing -masing adalah: (a - b), (-3m - n) dan (5x + y). Seperti yang dapat dilihat segera, perbedaannya ada pada tanda.

Gambar 1. Binomial dan binomalnya terkonjugasi. Mereka memiliki istilah yang sama, tetapi berbeda dalam tanda. Sumber: f. Zapata.

Binomial dikalikan dengan hasil konjugat dalam produk luar biasa yang banyak digunakan dalam aljabar dan sains. Hasil perkalian adalah pengurangan kotak dari istilah binomial asli.

Misalnya, (X - y) Itu adalah binomial dan konjugatnya (x + y). Kemudian, produk dari dua binomial adalah perbedaan kotak istilah:

(X - y).(x + y) = x² - Dan²

[TOC]

Bagaimana binomial terkonjugasi diselesaikan?

Aturan yang diucapkan dengan binomial terkonjugasi adalah sebagai berikut: 

Produk dari dua binomial konjugat sama dengan kuadrat istilah pertama dikurangi kuadrat dari istilah kedua. Hasil ini disebut perbedaan persegi.

Sebagai contoh aplikasi, kita akan mulai dengan menunjukkan hasil sebelumnya, yang dapat dilakukan dengan menggunakan properti distributif produk sehubungan dengan jumlah aljabar.

(x - y) (x + y) = x.x + x.dan dan.X - y.Dan

Perkalian sebelumnya diperoleh mengikuti langkah -langkah ini:

- Istilah pertama binomial pertama dikalikan dengan istilah pertama yang kedua

- Kemudian yang pertama dari yang pertama, untuk yang kedua dari yang kedua

- Kemudian yang kedua dari yang pertama untuk yang pertama 

- Akhirnya yang kedua dari yang pertama untuk yang kedua dari yang kedua.

Dapat melayani Anda: aljabar vektor

Sekarang mari kita buat perubahan kecil menggunakan properti komutatif: Dan.x = x.Dan. Tetap seperti ini:

(x - y) (x + y) = x.x + x.y - x.dan dan.Dan

Karena ada dua istilah yang sama tetapi sebaliknya (disorot dalam warna dan digarisbawahi), mereka dibatalkan dan disederhanakan:

(x - y) (x + y) = x.X - y.Dan

Akhirnya, diterapkan bahwa mengalikan angka dengan sendirinya, setara dengan mengangkatnya persegi, jadi X.x = x² dan juga Dan.y = y².

Dengan cara ini, apa yang telah ditunjukkan di bagian sebelumnya, bahwa produk dari jumlah untuk perbedaannya adalah perbedaan kotak:

(X - y).(x + y) = x² - Dan²

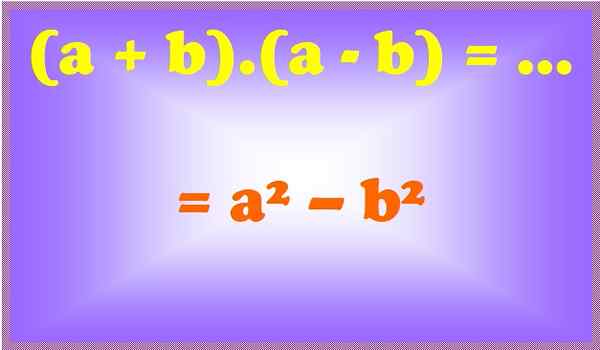Gambar 2. Jumlah untuk perbedaannya adalah perbedaan kotak. Sumber: f. Zapata.

Contoh

- Binomial terkonjugasi dari berbagai ekspresi

Contoh 1

Temukan konjugat (dan² - 3y).

Menjawab: (Dan² + 3y)

Contoh 2

Dapatkan produk (dan² - 3y) untuk konjugatnya.

Menjawab: (Dan² - 3y) (dan² + 3y) = (dan²)² - (3y)² = y⁴ - 3² Dan² = y⁴ - 9y²

Contoh 3

Kembangkan produk (1 + 2a).(2a -1).

Menjawab: Ekspresi sebelumnya setara dengan (2a + 1).(2a -1), yaitu, sesuai dengan produk binomial untuk konjugatnya.

Diketahui bahwa produk binomial untuk binomial terkonjugasinya sama dengan perbedaan kotak istilah binomial:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Contoh 4

Tulis produk (x + y + z) (x - y - z) sebagai perbedaan kotak.

Menjawab: Kita dapat mengasimilasi trinomial sebelum bentuk binomial terkonjugasi, memanfaatkan tanda kurung dan kurung persegi dengan cermat:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

Dengan cara ini perbedaan kotak dapat diterapkan:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Contoh 5

Ekspresikan produk (m² - m -1).(M² + m -1) sebagai perbedaan dalam kotak.

Dapat melayani Anda: 120 pembagi

Menjawab: Ekspresi sebelumnya adalah produk dari dua trinomial. Pertama, itu harus ditulis ulang sebagai produk dari dua binomial terkonjugasi:

(M² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - m].[(M² -1) +m)]

Kami menerapkan fakta bahwa produk binomial dengan konjugatnya adalah perbedaan kuadratik dari persyaratannya, seperti yang dijelaskan:

[(M² -1) - m].[(M² -1) +m)] = (m² -1)² - M²

Latihan

Seperti biasa, itu dimulai dengan latihan paling sederhana dan kemudian tingkat kompleksitas meningkat.

- Latihan 1

Escribca (9 - a²) sebagai produk.

Larutan

Pertama, kami menulis ulang ekspresi sebagai perbedaan kotak, untuk menerapkan apa yang dijelaskan sebelumnya. Karena itu:

(9 - a²) = (3² - ke²)

Kami segera menjadi faktor, yang setara dengan menulis perbedaan kotak ini sebagai produk, seperti yang diminta dalam pernyataan:

(9 - a²) = (3² - ke²) = (3 + a) (3 -a)

- Latihan 2

Faktorisasi 16x² - 9y⁴.

Larutan

Faktor ekspresi berarti menulisnya sebagai produk. Dalam hal ini, perlu untuk menulis ulang ekspresi sebelumnya, untuk mendapatkan perbedaan kotak.

Tidak sulit untuk melakukannya, karena mengamati dengan cermat, semua faktor adalah kotak yang sempurna. Misalnya 16 adalah kuadrat 4, 9 adalah kuadrat 3, Dan⁴ adalah kuadrat Dan² Dan X² adalah kuadrat X:

16x² - 9y⁴  = 4²X² - 3²Dan⁴ = 4²X²  - 3²(Dan²)²

Maka yang sudah kita ketahui diterapkan: bahwa perbedaan dalam kotak adalah produk dari binomial terkonjugasi:

(4x)² - (3 dan²)² = (4x - 3 dan²) . (4x + 3 dan²)

- Latihan 3

Tulis (A - B) sebagai produk binomial

Larutan

Perbedaan sebelumnya harus ditulis sebagai perbedaan persegi

(√a)² -(√b)²

Maka diterapkan bahwa perbedaan dalam kotak adalah produk dari binomial terkonjugasi

Dapat melayani Anda: pengurangan istilah serupa

(√a - √b) (√a + √b)

- Latihan 4

Salah satu penggunaan binomial terkonjugasi adalah rasionalisasi ekspresi aljabar. Prosedur ini terdiri dalam menghilangkan akar penyebut ekspresi fraksional, yang pada banyak kesempatan memfasilitasi operasi. Itu diminta untuk menggunakan binomial terkonjugasi untuk merasionalisasi ekspresi berikut:

√ (2 -x) / [√3 - √ (2+x)]]

Larutan

Yang pertama adalah mengidentifikasi binomial terkonjugasi dari penyebut: [√3 + √ (2 + x)]].

Sekarang kami mengalikan pembilang dan penyebut ekspresi asli dengan binomial terkonjugasi:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)]].[√3 + √ (2 + x)]

Dalam penyebut ekspresi sebelumnya, kami mengenali produk dari perbedaan dengan jumlah, yang sudah kita ketahui yang sesuai dengan perbedaan kotak binomial:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Menyederhanakan penyebutnya adalah:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Sekarang kami menjaga pembilang, yang akan menerapkan properti distributif produk sehubungan dengan jumlah:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

Dalam ungkapan sebelumnya kami mengenali produk binomial (2-X) untuk konjugatnya, yang merupakan produk luar biasa yang sama dengan perbedaan kotak kotak. Dengan cara ini ekspresi yang dirasionalisasi dan disederhanakan akhirnya diperoleh:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Latihan 5

Kembangkan produk berikut, menggunakan sifat -sifat binomial terkonjugasi:

[2^{(x + 3y)} - 3^{(x - 3y)}].[2^{(x + 3y)} + 3^{(x - 3y)}]

Larutan

4^{(2x + 6y)} - Ke -9^{(2x - 6y)} = 4a^(2x) .ke^(6y) - Ke -9^(2x) .ke^(-6y)= [4a^(6y) - Ke -9^(-6y)] .ke^(2x)

Pembaca yang penuh perhatian akan memperhatikan faktor umum yang telah disorot dalam warna.

Referensi

1. Baldor, a. 1991. Aljabar. Editorial Budaya Venezuela S.KE.
2. González J. Latihan binomial terkonjugasi. Pulih dari: akademi.Edu.
3. Matematika Alex. Produk yang luar biasa. Pulih dari youtube.com.
4. Math2me. Binomial terkonjugasi/ produk terkenal. Pulih dari youtube.com.
5. Produk binomial terkonjugasi. Dipulihkan dari: LMS.Colbachenlinea.MX.
6. Vital. Binomial terkonjugasi. Dipulihkan dari: YouTube.com.