Konsep konsep gratis, persamaan, latihan diselesaikan

Itu jatuh bebas Itu adalah gerakan vertikal yang dialami suatu objek saat dijatuhkan dari ketinggian tertentu di dekat permukaan bumi. Ini adalah salah satu gerakan paling sederhana dan paling langsung yang diketahui: dalam garis lurus dan dengan akselerasi konstan.

Semua objek yang dijatuhkan, atau yang dilemparkan secara vertikal ke atas atau ke bawah, bergerak dengan akselerasi 9.8 m/s² disediakan oleh tingkat keparahan bumi, terlepas dari massanya.

Jatuh bebas dari tebing. Sumber: Pexels.com.

Fakta ini dapat diterima hari ini tanpa masalah. Namun, memahami sifat sebenarnya dari kejatuhan bebas memakan waktu. Orang -orang Yunani telah menggambarkannya dan ditafsirkan pada dasarnya menuju abad keempat A C.

[TOC]

Persamaan Gerakan Musim Gugur Bebas

Setelah yakin bahwa akselerasi adalah sama untuk semua badan yang dilepaskan di bawah aksi gravitasi, sekarang saatnya untuk menetapkan persamaan yang diperlukan untuk menjelaskan gerakan ini.

Penting untuk menekankan bahwa resistensi udara tidak diperhitungkan dalam model gerakan pertama ini. Namun, hasil model ini sangat tepat dan dekat dengan kenyataan.

Dalam segala hal berikut, model partikel akan dianggap, yaitu dimensi objek tidak diperhitungkan, dengan asumsi bahwa seluruh massa terkonsentrasi dalam satu titik.

Untuk gerakan bujursangkar yang dipercepat secara seragam, itu dianggap sebagai sumbu referensi ke sumbu dan. Perasaan positif diambil dan negatifnya turun.

Besarnya kinematik

Dengan cara ini, persamaan posisi, kecepatan dan akselerasi tergantung pada waktunya adalah:

Percepatan

A = g = -9.8 m/s² (-32 kaki/s²)

Posisi tergantung waktu: dan T)

y = y_{salah satu} + v_{salah satu} . T + ½ gt²

Dimana dan_{salah satu} Itu adalah posisi awal ponsel dan v_{salah satu} adalah kecepatan awal. Ingatlah bahwa dalam peluncuran vertikal kecepatan awal tentu berbeda dari 0.

Yang bisa ditulis sebagai:

dan dan_{salah satu} = v_{salah satu} . T + ½ gt²

Δy = v_{salah satu} . T + ½ gt²

Dengan δDan menjadi perpindahan yang dilakukan oleh partikel seluler. Dalam satuan sistem internasional, baik posisi dan perpindahan diberikan dalam meter (m).

Kecepatan tergantung waktu: V (t)

V = V_{salah satu} + G . T

Kecepatan tergantung pada perpindahan

Dimungkinkan untuk menyimpulkan persamaan yang menghubungkan perpindahan dengan kecepatan, tanpa intervensi waktu. Untuk melakukan ini, waktu persamaan terakhir dibersihkan:

Dapat melayani Anda: model mekanik kuantum atom

 Dan diganti dalam persamaan perpindahan:

Δy = v_{salah satu} . T + ½ gt²

Kotak dikembangkan dengan bantuan produk dan ketentuan yang luar biasa.

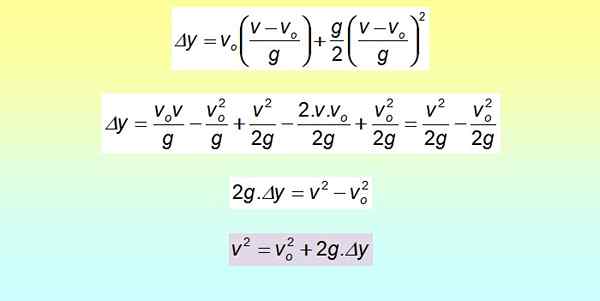
Persamaan ini berguna ketika waktu tidak tersedia, tetapi sebaliknya ada kecepatan dan perpindahan, seperti yang akan dilihat pada bagian dari contoh yang diselesaikan.

Contoh Free Fall

Pembaca yang penuh perhatian akan memperhatikan keberadaan kecepatan awal v_{salah satu}. Persamaan sebelumnya valid untuk gerakan vertikal di bawah aksi gravitasi, baik ketika objek jatuh dari ketinggian tertentu, seolah -olah dilemparkan secara vertikal ke atas atau ke bawah.

Saat objek turun, itu hanya selesai v_{salah satu} = 0 dan persamaan disederhanakan sebagai berikut.

Percepatan

A = g = -9.8 m/s² (-32 kaki/s²)

Posisi tergantung waktu: dan T)

y = y_{salah satu}+ ½ gt²

Kecepatan tergantung waktu: V (t)

v = g . T

Kecepatan tergantung pada perpindahan

v² = 2g. Dy

Dy Itu juga akan negatif, karena v² Itu pasti jumlah positif. Ini akan terjadi baik jika asal salah satu nol dari sistem koordinat di titik peluncuran atau di tanah.

Jika pembaca lebih suka, itu bisa mengambil arah ke bawah sebagai positif. Gravitasi akan terus bertindak jika diperkirakan itu + 9.8 m/s². Tetapi Anda harus konsisten dengan konvensi tanda -tanda yang dipilih.

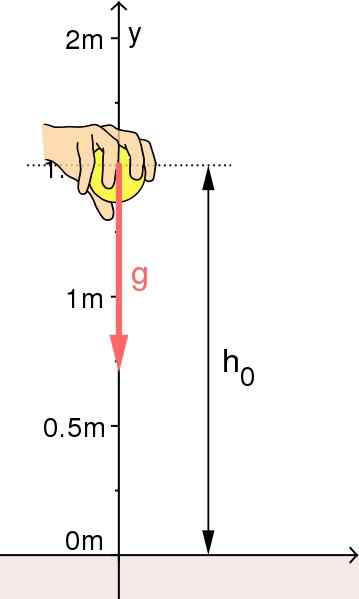Free Fall of suatu objek: Asal usul sistem referensi telah dipilih di tanah. Sumber: Sumber: Mikerun [CC BY-SA 4.0 (https: // createveCommons.Org/lisensi/by-sa/4.0)]

Peluncuran vertikal

Di sini, tentu saja, kecepatan awal tidak bisa nol. Kita harus memberikan objek untuk dorongan untuk naik. Menurut kecepatan awal yang diberikan, objek akan naik ke ketinggian yang lebih besar atau lebih kecil.

Tentu saja, akan ada momen di mana objek berhenti sejenak. Maka ketinggian maksimum akan tercapai sehubungan dengan titik peluncuran. Juga percepatan masih g down. Mari kita lihat apa yang terjadi dalam kasus ini.

Perhitungan ketinggian maksimum tercapai

Memilih saya = 0:

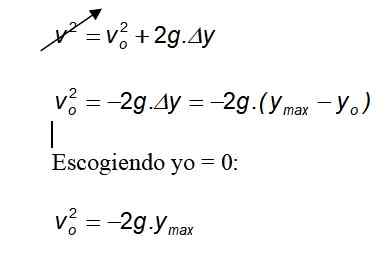
Karena gravitasi selalu menunjuk ke tanah ke arah negatif, tanda negatif dibatalkan.

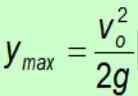
Perhitungan waktu maksimum

Prosedur serupa berfungsi untuk menemukan waktu yang dibutuhkan objek untuk mencapai ketinggian maksimum.

V = V_{salah satu} + G . T

Itu benar V = 0

v_{salah satu} = - g . T_Max

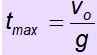
Waktu penerbangan adalah waktu di mana objek bertahan di udara. Jika objek kembali ke titik awal, waktu naik sama dengan waktu keturunan. Oleh karena itu, waktu penerbangan adalah 2. T maks.

Dapat melayani Anda: Skala Mikroskopis: Properti, Partikel Hitung, Contoh

Adalah dua kali t_Max Total waktu yang dilakukan objek di udara? Ya, selama objek dimulai dari suatu titik dan kembali ke sana.

Jika peluncuran dibuat dari ketinggian tertentu di tanah dan objek diizinkan untuk melanjutkan ini, waktu penerbangan tidak akan lagi dua kali lipat waktu maksimum.

Latihan terpecahkan

Dalam resolusi latihan yang mengikuti, berikut ini akan dipertimbangkan:

1-ketinggian dari mana objek dijatuhkan kecil dibandingkan dengan jari-jari bumi.

2-resistensi udara tercela.

3-Nilai percepatan gravitasi adalah 9.8 m/s²

4-ketika itu masalah dengan satu ponsel, lebih disukai dipilih dan_{salah satu} = 0 di titik awal. Ini biasanya memfasilitasi perhitungan.

5-AT kurang dari sebaliknya diindikasikan, arah ke atas dianggap positif.

6 -Dalam gerakan kombinasi naik dan turun, persamaan yang diterapkan secara langsung menawarkan hasil yang benar, selama konsistensi dipertahankan dengan tanda -tanda: naik secara positif, turun negatif dan keparahan -9.8 m/s² atau -10 m/s² Jika Anda lebih suka bundar (untuk lebih kenyamanan saat menghitung).

Latihan 1

Sebuah bola dilemparkan secara vertikal dengan kecepatan 25.0 m/s. Jawab pertanyaan berikut:

a) Berapa banyak yang naik?

b) Berapa lama waktu yang dibutuhkan untuk mencapai titik tertinggi?

c) Berapa lama bola yang dibutuhkan untuk menyentuh permukaan bumi setelah mencapai titik tertinggi?

d) Berapa kecepatan Anda saat Anda kembali ke tingkat di mana ia memulai?

Larutan

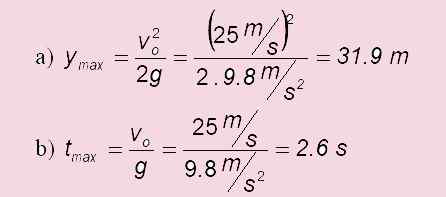
c) Dalam kasus peluncuran level: T_penerbangan = 2 . T_Max = 2 x6 s = 5.1 s

d) Ketika kembali ke titik awal kecepatan memiliki besarnya sama dengan kecepatan awal tetapi arah yang berlawanan, oleh karena itu harus - 25 m/s. Itu mudah diperiksa dengan mengganti nilai dalam persamaan untuk kecepatan:

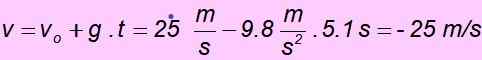
Latihan 2

Koper pos kecil dilepaskan dari helikopter yang turun dengan kecepatan konstan 1.50 m/s. Setelah 2.00 s Hitung:

a) Berapa kecepatan koper?

b) Seberapa jauh koper di bawah helikopter?

c) Apa jawaban Anda untuk bagian a) dan b) jika helikopter naik dengan kecepatan konstan 1.50 m/s?

Larutan

Bagian a

Saat meninggalkan helikopter, kopernya membawa kecepatan awalnya, oleh karena itu v_{salah satu} = -1.50 m/s. Dengan waktu yang ditunjukkan, kecepatan telah meningkat berkat percepatan gravitasi:

Dapat melayani Anda: benda selestial

V = V_{salah satu} + G . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Bagian b

Mari kita lihat seberapa banyak kopernya turun sehubungan dengan titik awal pada waktu itu:

Koper: Dy = v_{salah satu} . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Itu telah dipilih Dan_{salah satu} = 0 Di titik awal, seperti yang ditunjukkan pada awal bagian. Tanda negatif menunjukkan bahwa koper telah turun 22. 6 m di bawah titik awal.

Sementara itu helikopter Itu telah jatuh dengan cepat -1.50 m/s, kami berasumsi terus -menerus, oleh karena itu dalam waktu yang ditunjukkan 2 detik, helikopter telah melakukan perjalanan:

Helikopter: δy = v_{salah satu}.t = -1.lima puluh x 2 m = -3 m.

Oleh karena itu setelah 2 detik, koper dan helikopter dipisahkan oleh jarak dari:

D =| -22.6 - (-3) | M = 19. 6 m.

Jarak selalu positif. Untuk menyoroti fakta ini, nilai absolut digunakan.

Bagian c

Saat helikopter naik, ia memiliki kecepatan + 1.5 m/s. Dengan kecepatan itu koper keluar, sehingga setelah 2 detik sudah membawa:

V = V_{salah satu} + G . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Kecepatan ternyata negatif, karena setelah 2 detik koper bergerak ke bawah. Telah meningkat berkat gravitasi, tetapi tidak sebanyak di bagian a.

Sekarang kita akan menemukan berapa banyak koper yang turun sehubungan dengan titik awal selama 2 detik pertama perjalanan:

Valija: δy = v_{salah satu} . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Sementara itu, helikopter Itu telah bangkit Mengenai titik awal, dan telah melakukannya dengan kecepatan konstan:

Helikopter: δy = v_{salah satu}.T = +1.lima puluh x 2 m = +3 m.

Setelah 2 detik koper dan helikopter dipisahkan oleh jarak dari:

D =| -16.6 - (+3) | M = 19.6 m

Jarak yang memisahkan mereka sama dalam kedua kasus. Koper menempuh jarak yang lebih sedikit dalam kasus kedua, karena kecepatan awalnya diarahkan ke atas.

https: // youtu.BE/W2UVETXWSFK

Referensi

1. Kirkpatrick, l. 2007. Fisika: Pandangan Dunia. 6^ta Edisi Singkat. Pembelajaran Cengage.  23 - 27.
2. Rex, a. 2011. Dasar -dasar fisika. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14^th. Ed. Volume1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Dasar -dasar fisika. 9^na Ed. Pembelajaran Cengage. 43 - 55.
5. Wilson, J. 2011. Fisika 10. Pendidikan Pearson. 133 - 149.