Beban aksial bagaimana latihan yang dihitung dan diselesaikan

Itu Beban aksial Itu adalah gaya yang diarahkan secara paralel dengan sumbu simetri elemen yang membentuk struktur. Gaya atau beban aksial dapat berupa ketegangan atau kompresi. Jika garis aksi gaya aksial bertepatan dengan sumbu simetri yang melewati centroid elemen yang dipertimbangkan maka dikatakan bahwa itu adalah beban atau gaya aksial konsentris.

Sebaliknya, jika itu adalah gaya aksial atau beban yang sejajar dengan sumbu simetri, tetapi yang garis tindakannya tidak pada sumbu itu sendiri, itu adalah gaya aksial eksentrik yang eksentrik.

Gambar 1. Beban aksial. Sumber: Made sendiri

Pada Gambar 1 panah kuning mewakili gaya atau beban aksial. Dalam satu kasus itu adalah gaya tegang konsentris dan yang lain kami menghadapi gaya kompresi eksentrik.

Unit ukuran beban aksial dalam sistem internasional jika itu adalah Newton (n). Tetapi unit kekuatan lain seperti kilogram-force (kg-f) dan kekuatan pound (lb-f) sering digunakan (lb-f).

[TOC]

Bagaimana itu dihitung?

Untuk menghitung nilai beban aksial dalam elemen struktur, langkah -langkah berikut harus diikuti:

- Buat diagram gaya pada setiap elemen.

- Terapkan persamaan yang menjamin keseimbangan translasi, yaitu, bahwa jumlah semua kekuatan tidak berlaku.

- Pertimbangkan persamaan torsi atau momen sehingga keseimbangan rotasi terpenuhi. Dalam hal ini jumlah semua torsi harus nol.

- Hitung gaya, serta mengidentifikasi gaya aksial atau beban di masing -masing elemen.

Hubungan beban aksial dengan upaya normal

Upaya normal rata -rata didefinisikan sebagai hasil bagi antara beban aksial yang dibagi antara penampang area. Unit upaya normal dalam sistem internasional s.yo. Mereka adalah Newton di meter persegi (N/ m²) atau Pascal (PA). Gambar 2 menggambarkan konsep upaya normal untuk kejelasan.

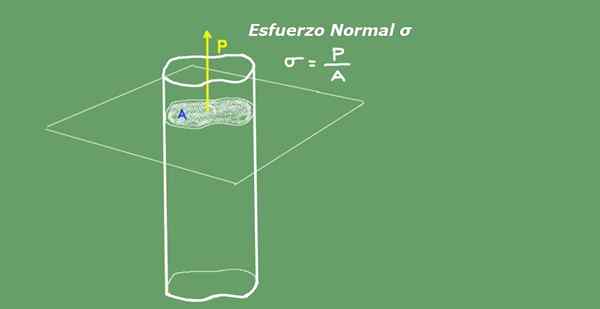Gambar 2. Upaya normal. Sumber: Made sendiri.

Latihan terpecahkan

-Latihan 1

Pertimbangkan kolom beton silinder H dan Radio R. Asumsikan bahwa kepadatan beton adalah ρ. Kolom tidak mendukung beban tambahan apa pun dari beratnya sendiri dan didukung pada dasar persegi panjang.

- Temukan nilai beban aksial pada titik A, B, C dan D, yang berada di posisi berikut: A di dasar kolom, b a ⅓ ketinggian h, c a ⅔ ketinggian h dan pada terakhir d di ujung atas kolom.

- Juga menentukan upaya normal rata -rata di masing -masing posisi ini. Ambil nilai numerik berikut: h = 3m, r = 20cm dan ρ = 2250 kg/m³

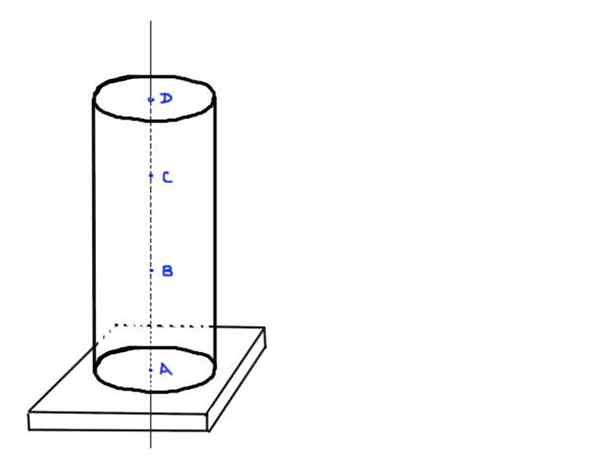Gambar 3. Kolom silindris. Sumber: Made sendiri.

Larutan

Total berat kolom

Bobot total W kolom adalah produk dari kepadatannya dengan volume dikalikan dengan percepatan gravitasi:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Beban aksial di a

Pada titik ke kolom ia harus mendukung seluruh bobotnya sehingga beban aksial pada titik ini adalah kompresi sama dengan berat kolom:

Pa = w = 8313 n

Beban aksial di b

Pada titik B akan sendirian ⅔ dari kolom, sehingga beban aksial pada titik itu akan menjadi kompresi dan nilai ⅔ dari berat kolom:

Pb = ⅔ w = 5542 n

Gambar 3. Kolom silindris. Sumber: Made sendiri.

Di atas posisi C hanya ada kolom ⅓, sehingga beban kompresi aksalnya akan ⅓ dengan beratnya sendiri:

Pc = ⅓ w = 2771 n

Beban aksial di d

Akhirnya pada titik D yang merupakan ujung atas kolom tidak ada beban, jadi gaya aksial pada titik itu batal.

PD = 0 n

Upaya normal di setiap posisi

Untuk menentukan upaya normal di masing -masing posisi, akan diperlukan untuk menghitung penampang area A, yang diberikan oleh:

A = π ∙ r² = 0,126m²

Dengan cara ini, upaya normal di masing -masing posisi akan menjadi hasil bagi antara gaya aksial di masing -masing titik yang dibagi antara penampang yang sudah dihitung, yang dalam latihan ini sama untuk semua titik karena merupakan kolom silinder silinder kolom.

σ = p/a; σa = 66.15 kPa; σb = 44,10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Latihan 2

Gambar tersebut menunjukkan struktur yang terdiri dari dua batang yang akan kami sebut AB dan CB. AB Bar didukung di ujung satu melalui pin dan di ujung lain terhubung ke bilah lainnya melalui b -pin lain.

Demikian pula, bilah CB didukung di ujung C dengan menggunakan pin dan di ujung B dengan pin B yang menyatukannya ke bar lainnya. Gaya vertikal atau beban F diterapkan pada pin B seperti yang ditunjukkan seperti gambar berikut menunjukkan:

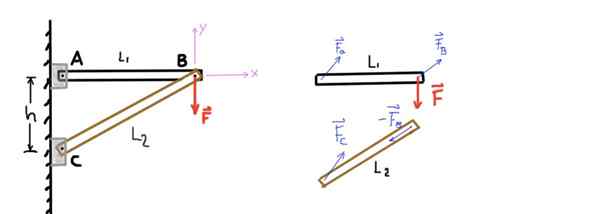Gambar 4. Dua batang struktur dan diagram tubuh bebas. Sumber: Made sendiri.

Asumsikan berat batang tercela, karena gaya f = 500 kg-f jauh lebih besar dari berat struktur. Pemisahan antara dukungan A dan C adalah H = 1,5 m dan panjang batang AB adalah L1 = 2 m. Tentukan beban aksial di masing -masing batang, menunjukkan apakah itu kompresi aksial atau beban tegangan.

Solusi 2

Gambar tersebut menunjukkan, melalui diagram tubuh bebas, kekuatan yang bekerja pada masing -masing elemen struktur. Sistem koordinat cartesian juga ditunjukkan dengan mana persamaan ekuilibrium akan dinaikkan.

Torsi atau momen akan dihitung pada titik B dan akan dianggap positif jika mereka menunjukkan keluar dari layar (sumbu z). Keseimbangan kekuatan dan torsi untuk setiap bilah adalah:

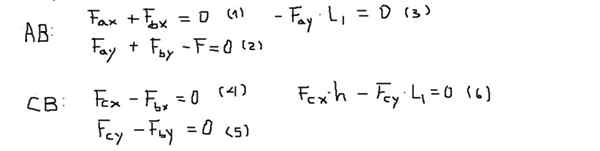
Kemudian komponen kekuatan masing -masing persamaan jelas mengikuti urutan berikut:

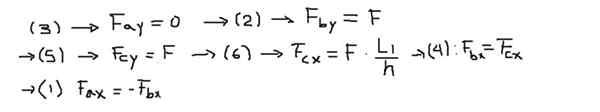
Akhirnya, kekuatan yang dihasilkan dihitung di ujung setiap batang:

Dapat dicatat bahwa kekuatan di ujung masing -masing batang sejajar dengan mereka, menegaskan bahwa itu adalah kekuatan atau beban aksial. Dalam kasus bilah AB, itu adalah gaya tegangan aksial yang nilainya:

F ∙ (l1/h) = 500 kg-f ∙ (2.0m/1.5m) = 666.6 kg-f = 6533.3 n

Bilah CB sedang dalam kompresi karena dua kekuatan yang bertindak pada ujungnya yang sejajar dengan bar dan menunjuk ke tengah mereka. Besarnya gaya kompresi aksial di bilah CB adalah:

F ∙ (1 + l1²/h²) 1/2 = 500 kg-f ∙ (1 + (2/1.5) ²) 1/2 = 833.3 kg-F = 8166.6 N

Referensi

1. Bir f ... mekanika material. Ke -5. Edisi. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mekanika Bahan. Edisi Kedelapan. Prentice Hall. 2011. 3-60.
3. Gere J. Mekanika Bahan. Edisi Kedelapan. Pembelajaran Cengage. 4-220.
4. Giancoli, d. 2006. Fisika: Prinsip dengan aplikasi. Edisi ke -6. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Catatan Fisika Umum. Unam. 87-98.