Pusat Properti Gravitasi, Perhitungan, Contoh

Dia pusat gravitasi dari ukuran ukuran yang terukur adalah titik di mana beratnya dianggap diterapkan. Oleh karena itu adalah salah satu konsep utama statis.

Pendekatan pertama dalam masalah fisika dasar adalah dengan mengasumsikan bahwa objek apa pun berperilaku sebagai massa tertentu, yaitu, tidak memiliki dimensi dan seluruh massa terkonsentrasi dalam satu titik tunggal. Ini berlaku untuk kotak, mobil, planet atau partikel subatomik. Model ini dikenal sebagai model partikel.

Gambar 1. Di ketinggian melompat, atlet memperbaikinya sehingga pusat gravitasi berada di luar tubuh. Sumber: Pixabay

Secara alami ini adalah pendekatan, yang memberikan hasil yang sangat baik untuk banyak aplikasi. Bukan tugas yang mudah untuk mempertimbangkan perilaku individu dari ribuan dan jutaan partikel yang dapat dikandung oleh objek apa pun.

Namun, dimensi nyata dari hal -hal harus diperhitungkan jika Anda mau. Karena kita biasanya berada di sekitar bumi, kekuatan yang selalu ada pada tubuh apa pun justru.

[TOC]

Pertimbangan untuk menemukan pusat gravitasi 

Jika ukuran tubuh akan diperhitungkan, di mana beratnya akan diterapkan secara khusus? Ketika Anda memiliki objek kontinu secara sewenang -wenang, beratnya adalah a Kekuatan terdistribusi di antara masing -masing partikel konstituennya.

Biarkan partikel -partikel ini m₁, M₂, M₃... masing -masing dari mereka mengalami gaya gravitasi yang sesuai₁g, m₂g, m₃G ..., semuanya paralel. Begitulah, karena medan gravitasi bumi dianggap konstan dalam sebagian besar kasus, mengingat fakta bahwa benda kecil dibandingkan dengan ukuran planet ini dan dekat dengan permukaannya.

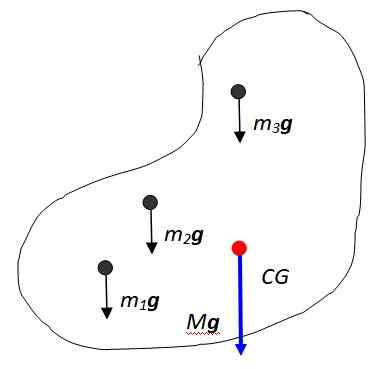Gambar 2. Berat objek adalah massa terdistribusi. Sumber: Made sendiri.

Jumlah vektor dari gaya -kekuatan ini menghasilkan berat objek, diterapkan pada titik yang disebut pusat gravitasi yang dilambangkan dalam gambar sebagai CG, yang kemudian bertepatan dengan Pusat Massa. Pusat massa pada gilirannya adalah titik di mana seluruh massa dapat dianggap terkonsentrasi.

Berat yang dihasilkan memiliki besarnya Mg Di mana M Itu adalah massa total objek, dan tentu saja diarahkan secara vertikal ke pusat bumi. Notasi Sumory berguna untuk mengekspresikan tubuh total tubuh:

Objek simetris dan homogen, yang setara dengan kepadatannya seragam, memiliki pusat gravitasi di pusat geometris: kubus, paralelepiped, cincin, ban atau bola.

Pusat gravitasi tidak selalu cocok dengan titik material. Misalnya, CG dari lingkaran ada di pusat geometrisnya, di mana tidak ada adonan itu sendiri. Meski begitu, jika Anda ingin menganalisis kekuatan yang bertindak pada lingkaran, bobot harus diterapkan pada titik yang tepat ini.

Dalam kasus di mana objek tersebut sewenang -wenang, jika homogen, pusat massanya masih dapat dihitung dengan menemukan Centroid o Baricentro sosok itu.

Dapat melayani Anda: Merkurius (planet)

Bagaimana pusat gravitasi dihitung?

Pada prinsipnya jika pusat gravitasi (CG) dan pusat massa (CM) bertepatan ketika medan gravitasi seragam, maka CM dapat dihitung dan di atasnya menerapkan berat.

Pertimbangkan dua kasus: yang pertama adalah satu di mana distribusi massa bijaksana; yaitu, Anda dapat menghitung setiap massa yang membentuk sistem dan menetapkan angka I, seperti yang dilakukan pada contoh sebelumnya.

Koordinat pusat massa untuk distribusi massa diskrit adalah: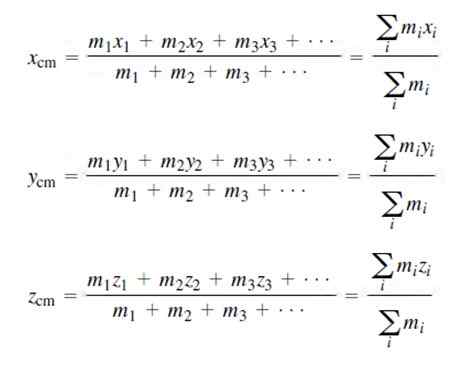

Secara alami jumlah semua massa setara dengan massa total sistem M, seperti yang ditunjukkan di atas.

Tiga persamaan dikurangi menjadi bentuk kompak saat mempertimbangkan vektor r_cm o Posisi vektor pusat massa:

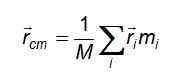
Dan dalam hal distribusi massa kontinu, di mana partikel -partikel memiliki ukuran diferensial dan tidak dapat dibedakan untuk menghitungnya, jumlahnya digantikan oleh integral yang dibuat tentang volume yang ditempati oleh objek yang dimaksud:

Di mana R Itu adalah vektor posisi massa diferensial DM Dan definisi kepadatan massa untuk mengekspresikan diferensial massa telah dibuat DM terkandung dalam diferensial volume Dv:

Kepadatan objek bisa konstan, dalam hal ini keluar dari integral, atau menjadi fungsi dari koordinat spasial dan kita harus mengetahui ketergantungannya pada (x, y, z) untuk menyelesaikan integral.

Properti

Beberapa pertimbangan penting tentang pusat massa adalah sebagai berikut:

- Meskipun sistem referensi diperlukan untuk menetapkan posisi, pusat massa tidak bergantung pada pilihan yang dibuat dari sistem, karena merupakan properti dari objek.

- Ketika objek memiliki sumbu atau bidang simetri, pusat massa berada pada sumbu atau bidang tersebut. Manfaatkan keadaan ini menghemat waktu perhitungan.

- Semua kekuatan eksternal yang bekerja pada objek dapat diterapkan ke pusat massa. Mengikuti jalur hal ini memberikan gagasan global tentang pergerakan objek dan memfasilitasi pekerjaan mempelajari perilakunya.

-Menemukan pusat gravitasi tubuh dalam keseimbangan statis

Misalkan tubuh dari gambar sebelumnya berada dalam keseimbangan statis adalah.

Gambar 3. Skema untuk menghitung torsi berat sehubungan dengan titik atau.

Momen torsi bersih sehubungan dengan O, menurut Gambar 3 adalah: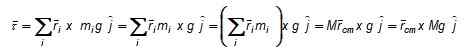Gaya F yang diterapkan secara vertikal di tengah gravitasi (atau juga di atas atau di bawah, pada sumbu yang melewati itu) akan menghasilkan torsi yang berlawanan yang akan mencegah rotasi objek dan mempertahankan keseimbangan rotasi. Besarnya F dipilih sehingga objek tidak ditransfer dan dengan cara ini kita akan memilikinya dalam keseimbangan statis.

Dapat melayani Anda: optik bergelombang

-Contoh terpecahkan

Batang tipis bahan seragam memiliki panjang 6 m dan berat 30 N. Pada akhirnya, 50 N barat dan yang lain 20 N di ujung kanannya digantung. Temukan: a) Besarnya gaya naik yang diperlukan untuk menjaga keseimbangan batang, b) pusat gravitasi set.

Larutan

Diagram gaya ditunjukkan pada gambar berikut. Berat batang diterapkan di pusat gravitasi, yang bertepatan dengan pusat geometrisnya. Satu -satunya dimensi bilah yang diperhitungkan adalah panjangnya, karena pernyataan itu menginformasikan bahwa itu tipis.

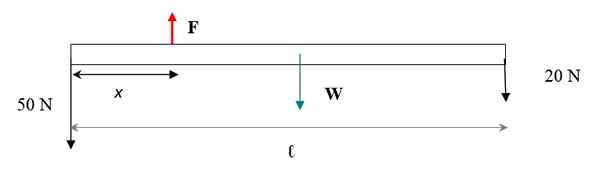Gambar 4. Diagram Pàra La Barra.

Agar sistem bobot + bobot tetap dalam keseimbangan terjemahan, jumlah kekuatan harus nol. Kekuatannya vertikal, jika kita mempertimbangkan dengan tanda + dan ke bawah dengan tanda - lalu:

F- 50- 20-30 N = 0

F = 100 n

Kekuatan ini menjamin keseimbangan terjemahan. Mengambil momen torsi semua kekuatan mengenai sumbu yang melewati ujung kiri sistem dan menerapkan definisi:

t = r x f

Saat -saat dari semua kekuatan ini sehubungan dengan titik yang dipilih tegak lurus terhadap bidang batang:

T_F = xf = 100x

T_W = -(l/2) mg = -3m . 30 n = -90 n.M

T₁ = 0 (Karena gaya 50 N melewati poros belokan yang dipilih dan tidak melatih momen)

T₂ = -Lf₂ = 6 m . 20 n = -120 n.M

Karena itu:

100 x -90 -120 n.m = 0

x = 2.10 m

Pusat gravitasi bar bar + bobot terletak di 2.10 meter dari ujung kiri bar.

Perbedaan dengan pusat massa

Pusat gravitasi bertepatan dengan pusat massa, seperti yang ditunjukkan, selama medan gravitasi tanah konstan untuk semua titik objek yang akan dipertimbangkan. Medan gravitasi bumi tidak lain adalah nilai g = 9 yang diketahui dan akrab.8 m/s² diarahkan ke bawah secara vertikal.

Meskipun nilai G mengalami variasi dengan garis lintang dan ketinggian, mereka biasanya tidak mempengaruhi objek yang sebagian besar waktu diperlakukan. Sangat berbeda jika dianggap sebagai tubuh besar di sekitar bumi, misalnya asteroid yang akan dekat dengan planet ini.

Asteroid memiliki pusat massanya sendiri, tetapi pusat gravitasi tidak lagi harus bertepatan dengan ini G Ini mungkin akan mengalami variasi besar dalam besarnya, mengingat ukuran asteroid dan bahwa bobot masing -masing partikel mungkin tidak paralel.

Perbedaan mendasar lainnya adalah bahwa pusat massa terlepas dari apakah ada kekuatan yang disebut bobot yang diterapkan pada objek. Ini adalah sifat intrinsik dari objek yang mengungkapkan bagaimana massanya didistribusikan dalam kaitannya dengan geometrinya.

Dapat melayani Anda: apa konstanta dielektrik?

Pusat massa ada baik jika ada berat yang diterapkan seolah -olah tidak. Dan terletak di posisi yang sama meskipun objek ditransfer ke planet lain di mana medan gravitasi berbeda.

Di sisi lain, pusat gravitasi jelas terkait dengan penerapan berat badan, karena kami telah dapat menghargai di seluruh paragraf sebelumnya.

Contoh Pusat Gravitasi

Pusat gravitasi objek yang tidak teratur

Sangat mudah untuk mengetahui di mana pusat gravitasi objek yang tidak teratur seperti cangkir. Pertama ditangguhkan dari titik mana pun dan dari sana garis vertikal ditarik (pada Gambar 5 itu adalah garis fuchsia di gambar kiri).

Kemudian ditangguhkan dari titik lain dan vertikal baru (garis pirus di gambar kanan) ditarik. Persimpangan kedua garis adalah pusat gravitasi cangkir.

Gambar 5 . Lokasi cangkir CG. Sumber: Pixabay yang dimodifikasi.

Keseimbangan objek

Mari kita analisis stabilitas truk yang beredar di sepanjang jalan. Saat pusat gravitasi berada di atas pangkal truk, itu tidak akan menuangkan. Gambar di sebelah kiri adalah posisi yang paling stabil.

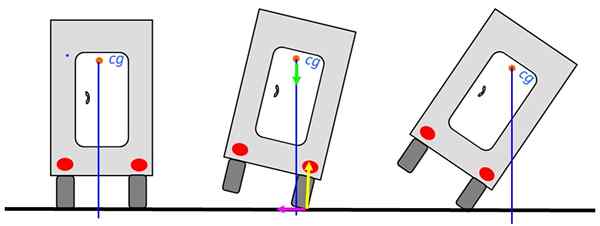Gambar 6. Saldo truk. Sumber: Made sendiri.

Bahkan ketika truk condong ke kanan dapat kembali ke posisi keseimbangan yang stabil, seperti pada gambar medium, karena vertikal masih melewati pangkalan. Namun, ketika garis ini lewat di luar truk akan berputar.

Diagram menunjukkan kekuatan pada titik pendukung: normal berwarna kuning, berat berwarna hijau dan gesekan statis di sebelah kiri di fuchsia. Normal dan Rubb. Oleh karena itu mereka tidak akan berkontribusi untuk membuang truk.

Bobot tetap ada, yang melakukan momen torsi, untungnya dalam pengertian anti -ador dan yang cenderung kembali ke truk ke posisi keseimbangannya. Perhatikan bahwa garis vertikal melewati permukaan pendukung, yang merupakan ban.

Saat truk berada di posisi kanan ekstrem, waktu torsi berat badan berubah dan menjadi ke arah yang tegang. Tidak bisa ditimbulkan di lain waktu, truk akan menuangkan.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.  247-253.
2. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6 ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fisik. Vol. 1. Edisi ke -3. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V. 331-341.
4. Rex, a. 2011. Dasar -dasar fisika. Pearson.146-155.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.340-346.