Tahap siklus Carnot, aplikasi, contoh, latihan

Dia Siklus Carnot Ini adalah urutan proses termodinamika yang terjadi di mesin Carnot, perangkat ideal yang hanya terdiri dari proses reversibel; yaitu, mereka yang, setelah terjadi, dapat kembali ke keadaan awal.

Jenis mesin ini dianggap ideal, karena tidak memiliki disipasi, gesekan atau viskositas yang muncul dalam mesin nyata, mengubah energi termal menjadi pekerjaan yang dapat digunakan, meskipun konversi tidak dilakukan 100%.

Gambar 1. Lokomotif uap. Sumber: Pixabay

Mesin dibangun berdasarkan zat yang mampu melakukan pekerjaan, seperti gas, bensin atau uap. Zat ini mengalami berbagai perubahan suhu dan pada gilirannya mengalami variasi dalam tekanan dan volumenya. Dengan cara ini dimungkinkan untuk memindahkan piston di dalam silinder.

[TOC]

Apa siklus Carnot?

Siklus Carnot terjadi dalam sistem yang disebut carnot atau c motor, yang merupakan gas ideal yang terkunci dalam silinder dan dilengkapi dengan piston, yang bersentuhan dengan dua sumber pada suhu yang berbeda t₁ dan T₂ seperti yang ditunjukkan pada gambar berikut di sebelah kiri.

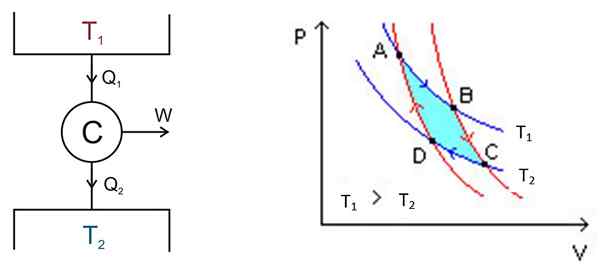Gambar 2. Di sebelah kiri skema mesin C arnot, di sebelah kanan diagram PV. Sumber gambar kiri: KETA - pekerjaan sendiri, CC oleh 2.5, https: // commons.Wikimedia.org/w/indeks.Php?Curid = 681753, gambar kanan Wikimedia Commons.

Ada proses berikut dalam mode kasar:

1. Sejumlah panas dipasok ke perangkat_{pintu masuk} = Q₁ Dari tangki termal pada t suhu tinggi₁.
2. Mesin Carnot C melakukan pekerjaan W berkat panas yang disediakan ini.
3. Sebagian panas yang digunakan: limbah q_KELUAR, Itu ditransfer ke tangki termal yang berada pada suhu yang lebih rendah₂.

Tahapan siklus Carnot

Analisis dibuat oleh diagram p -V (volume tekanan), seperti yang ditunjukkan pada Gambar 2 (gambar kanan). Tujuan motor bisa menjaga deposit termal 2 tetap dingin, mengekstraksi panas darinya. Dalam hal ini adalah a Mesin refrigeran. Jika sebaliknya Anda ingin memberikan panas ke deposit termal 1 maka itu adalah a Pompa panas.

Diagram P -V menunjukkan perubahan tekanan - suhu mesin dalam dua kondisi:

- Mempertahankan suhu konstan (proses isotermal).

- Tidak ada perpindahan panas (isolasi termal).

Dua proses isotermal perlu dihubungkan, yang dicapai dengan menggunakan isolasi termal.

Titik

Anda dapat mulai di titik mana pun dalam siklus, di mana gas memiliki tekanan, volume, dan kondisi suhu tertentu. Gas menderita serangkaian proses dan dapat kembali ke kondisi awal untuk memulai siklus lain, dan selalu energi internal akhir sama dengan yang awal. Karena energi dipertahankan:

Pekerjaan yang dilakukan oleh C = input panas - panas berangkat

ΔW = q_{pintu masuk} - Q_KELUAR

Area yang termasuk dalam siklus atau loop ini, dalam pirus dalam gambar, sama dengan pekerjaan yang dilakukan oleh mesin carnot.

Poin A, B, C dan D ditandai pada Gambar 2. Itu akan dimulai pada titik untuk mengikuti panah biru.

Tahap Pertama: Ekspansi Isotermal

Suhu antara titik A dan B adalah T₁. Sistem ini menyerap panas dari deposit termal 1 dan menderita ekspansi isotermal. Kemudian volume meningkat dan tekanan berkurang.

Namun, suhunya tetap di T₁, Sejak saat gas mengembang. Oleh karena itu, energi internalnya tetap konstan.

Ini dapat melayani Anda: Graff Van Generator: Pihak, Cara Kerjanya, Aplikasi

Tahap Kedua: Ekspansi adiabatik

Pada titik B, sistem memulai ekspansi baru di mana sistem tidak menang atau kehilangan panas. Ini dicapai dengan memasukkannya ke dalam isolasi kalori seperti yang ditunjukkan sebelumnya. Oleh karena itu adalah ekspansi adiabatik yang terus menunjuk C mengikuti panah merah. Volume meningkat dan tekanan berkurang hingga mencapai nilai terendah.

Tahap ketiga: Kompresi isotermal

Mulai dari titik C dan berakhir di D. Insulasi dihapus dan sistem bersentuhan dengan deposit termal 2, yang suhunya t₂ Itu kurang. Sistem menghasilkan limbah panas ke tangki termal, tekanan mulai meningkat dan volume berkurang.

Tahap Keempat: Kompresi Adiabatik

Tercapai ke titik D, sistem kembali ke isolasi termal, tekanan meningkat dan volume berkurang hingga mencapai kondisi asli titik a. Kemudian siklusnya diulang lagi.

Teorema Carnot

Teorema Carnot pertama kali dipostulatkan pada awal abad ke -19 oleh fisikawan Prancis Sadi Carnot. Pada tahun 1824 Carnot, yang merupakan bagian dari tentara Prancis, menerbitkan sebuah buku di mana ia mengusulkan jawaban atas pertanyaan berikut: dalam kondisi apa mesin termal memiliki efisiensi maksimal? Carnot kemudian menetapkan yang berikut:

Tidak ada mesin termal yang berjalan di antara dua deposit termal lebih efisien daripada mesin carnot.

Hasil η dari mesin termal diberikan oleh rasio antara pekerjaan yang dilakukan w dan panas yang diserap T:

kinerja = pekerjaan selesai/panas diserap

Dengan cara ini, kinerja mesin termal I adalah: η = w/q. Sementara kinerja mesin carnot r adalah η '= w/q', dalam kasus kedua mesin mereka dapat melakukan pekerjaan yang sama.

Teorema Carnot menyatakan bahwa η tidak pernah lebih besar dari η '. Kalau tidak, ia jatuh ke dalam kontradiksi dengan hukum kedua termodinamika, yang menurutnya suatu proses di mana hasilnya adalah panas dari tubuh dengan suhu yang lebih rendah tidak mungkin untuk pergi ke suhu lain yang lebih tinggi tanpa menerima bantuan eksternal. Karena itu:

η _< η^'

Demonstrasi Teorema Carnot

Untuk menunjukkan bahwa demikian, pertimbangkan mesin Carnot yang bertindak sebagai mesin kulkas yang digerakkan oleh mesin I. Ini dimungkinkan karena mesin Carnot bekerja dengan proses reversibel, sebagaimana ditentukan di awal.

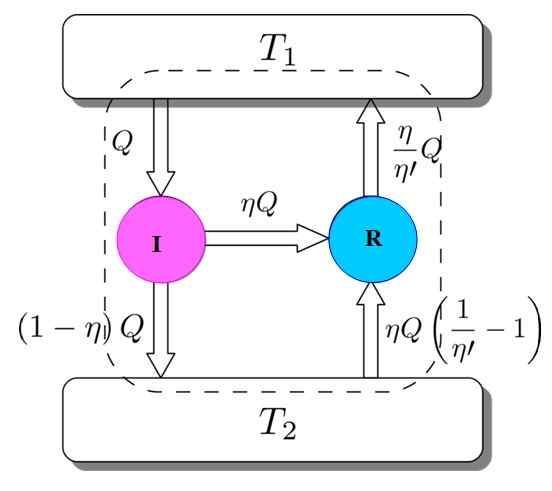
Gambar 3. Demonstrasi Teorema Carnot. Sumber: Netheril96 [CC BY-SA 3.0 (https: // createveCommons.Org/lisensi/by-sa/3.0)]

Anda memiliki keduanya: Saya dan r bekerja dengan deposit termal yang sama dan akan diasumsikan bahwa η _> η^'. Jika sepanjang jalan kontradiksi dicapai dengan hukum termodinamika kedua, teorema Carnot ditunjukkan dengan pengurangan absurditas.

Gambar 3 membantu mengikuti proses. Mesin I membutuhkan sejumlah panas Q, yang membelah dengan cara ini: melakukan pekerjaan pada R yang setara dengan w = ηq dan sisanya adalah panas yang ditransfer (1 -η) q ke tangki termal t₂.

Karena energi dipertahankan, semuanya terpenuhi:

DAN_{pintu masuk} = Q = kerja w + panas yang ditetapkan untuk t₂ = ηq + (1 -η) q = e_KELUAR

Sekarang mesin kulkas Carnot R mengambil tangki termal 2 sejumlah panas yang diberikan oleh:

Itu dapat melayani Anda: imantation: apa yang terdiri dari, metode, dan contoh

(η / η ') (1 -η') q =

Energi juga harus disimpan dalam kasus ini:

DAN_{pintu masuk} = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_KELUAR

Hasilnya adalah transfer ke tangki termal T₂ dari sejumlah panas yang diberikan oleh (η / η ') q = q'.

Jika η lebih besar dari η 'itu berarti bahwa deposit termal suhu tertinggi telah tiba lebih banyak panas daripada yang saya ambil semula. Karena tidak ada agen eksternal, seperti sumber termal lain, telah berpartisipasi, satu -satunya cara itu bisa terjadi adalah bahwa deposit termal terdingin menghasilkan panas.

Ini tidak setuju dengan hukum termodinamika kedua. Disimpulkan bahwa tidak mungkin bahwa η^' Jadilah kurang dari η, oleh karena itu mesin I tidak dapat memiliki lebih banyak kinerja daripada mesin carnot r.

Teorema akibat wajar dan keterbatasan

Teorema CARNOT Worollary menyatakan bahwa dua mesin Carnot memiliki efisiensi yang sama jika keduanya beroperasi dengan deposit termal yang sama.

Itu berarti bahwa zat itu tidak masalah, kinerja independen dan tidak dapat dinaikkan dengan mengubahnya.

Kesimpulan dari analisis sebelumnya adalah bahwa siklus Carnot adalah bagian atas proses termodinamika yang dapat dicapai secara ideal. Dalam praktiknya ada banyak faktor yang mengurangi efisiensi, misalnya fakta bahwa isolasi tidak pernah sempurna dan pada tahap adiabatik sebenarnya ada pertukaran kalori dengan eksterior.

Dalam kasus mobil, blok mesin dipanaskan. Di sisi lain, campuran gas dan udara tidak berperilaku persis seperti gas yang ideal, yang merupakan titik awal dari siklus Carnot. Ini hanya menyebutkan beberapa faktor yang akan menyebabkan pengurangan kinerja drastis.

Contoh

Piston di dalam silinder

Jika sistem adalah piston yang terkunci dalam silinder seperti pada Gambar 4, piston naik selama ekspansi isotermal, seperti yang dapat dilihat dalam skema pertama kiri ekstrem dan juga naik selama ekspansi adiabatik.

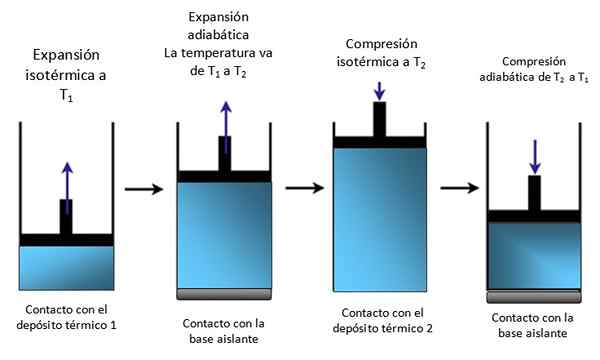Gambar 4. Pergerakan piston di dalam silinder. Sumber: Made sendiri.

Kemudian terkompresi secara isotermis, memberikan panas, dan terus mengompres secara adiabatik. Hasilnya adalah gerakan di mana piston naik dan turun di dalam silinder dan dapat ditransmisikan ke bagian lain dari perangkat tertentu, seperti mesin mobil misalnya, yang menghasilkan pasangan, atau mesin beruap.

Berbagai proses reversibel

Selain ekspansi dan kompresi gas ideal di dalam silinder, ada proses reversibel ideal lainnya yang dapat dikonfigurasi oleh siklus Carnot, misalnya:

- Gerakan perjalanan pulang pergi tanpa adanya gesekan.

- Pegas ideal yang dikompresi dan didekompresi dan itu tidak pernah berubah bentuk.

- Sirkuit listrik di mana tidak ada resistensi yang menghilangkan energi.

- Siklus magnetisasi dan demagnetisasi di mana tidak ada kerugian.

- Memuat dan mengunduh baterai.

Pembangkit listrik tenaga nuklir

Meskipun ini adalah sistem yang sangat kompleks, pendekatan pertama dari apa yang diperlukan untuk menghasilkan energi dalam reaktor nuklir adalah yang mengikuti:

- Sumber termal, yang terdiri dari bahan yang hancur secara radioaktif seperti uranium.

Dapat melayani Anda: model atom saat ini

- Wastafel atau deposit termal dingin yang akan menjadi atmosfer.

- "Mesin Carnot" yang menggunakan cairan, hampir selalu mengalir, yang disediakan panas dari sumber termal untuk mengubahnya menjadi uap.

Saat siklus dilakukan, listrik diperoleh sebagai pekerjaan bersih. Saat diubah menjadi uap suhu tinggi, air tercapai ke turbin, di mana energi diubah menjadi gerakan atau energi kinetik.

Turbin pada gilirannya mengaktifkan generator listrik yang mengubah energi pergerakannya menjadi listrik. Selain bahan fistening seperti uranium, tentu saja bahan bakar fosil dapat digunakan sebagai sumber panas.

Latihan terpecahkan

-Contoh 1: Efisiensi mesin termal

Efisiensi mesin termal didefinisikan sebagai rasio antara pekerjaan output dan pekerjaan masuk, dan karenanya merupakan jumlah tanpa dimensi:

Efisiensi maksimum = (q_{pintu masuk} - Q _KELUAR) /Q_{pintu masuk}

Menunjukkan efisiensi maksimum sebagai e_Max, Dimungkinkan untuk menunjukkan ketergantungan suhunya, yang merupakan variabel termudah untuk diukur, seperti:

Dan_Max = 1 - (t₂/T₁)

Dimana t₂ Itu adalah suhu wastafel dan t₁ Itu adalah suhu sumber termal. Karena yang terakhir lebih besar, efisiensi selalu ternyata kurang dari 1.

Misalkan mesin termal mampu bekerja pada cara -cara berikut: a) antara 200 K dan 400 K, b) antara 600 K dan 400 K. Apa efisiensi dalam setiap kasus?

Larutan

a) Dalam kasus pertama efisiensinya adalah:

Dan_Max1 = 1 - (200/400) = 0.lima puluh

b) Untuk mode kedua, efisiensinya adalah:

Dan_Max2 = 1- (400/600) = 0.33

Meskipun perbedaan suhu sama antara kedua mode, efisiensi tidak. Dan yang lebih penting lagi adalah mode yang paling efisien beroperasi pada suhu yang lebih rendah.

-Contoh 2: Panas yang diserap dan panas yang diserap

Mesin termal 22 % menghasilkan 1530 J pekerjaan. Temukan: a) Jumlah panas yang diserap dari deposit termal 1, b) Jumlah panas yang dibuang ke tangki termal 2.

a) Dalam hal ini definisi efisiensi digunakan, karena pekerjaan yang dilakukan, bukan dari suhu endapan termal tersedia. Efisiensi 22% berarti E _Max = 0.22 karena itu: Oleh karena itu:

Efisiensi maksimum = kerja /q_{pintu masuk}

Jumlah panas yang diserap tepat Q_{pintu masuk}, Jadi kliring yang Anda miliki:

Q_{pintu masuk} = Kerja/efisiensi = 1530 j/0.22 = 6954.5 J

b) Jumlah panas yang ditugaskan ke tangki terdingin adalah dari ΔW = q_{pintu masuk} - Q_KELUAR

Q_KELUAR = Q_{pintu masuk} - ΔW = 6954.5 -1530 J = 5424.5 J.

Cara lain dari Dan_Max = 1 - (t₂/T₁). Karena suhu tidak diketahui, tetapi ini terkait dengan panas, efisiensi juga dapat dinyatakan sebagai:

Dan_Max = 1 - (q_Melesat/Q_terserap)

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 654-657
2. Energi nuklir. Pengoperasian pembangkit listrik tenaga nuklir. Pulih dari: nuklir energi.bersih
3. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage. 618-622.
4. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit MacGraw. 414-416.
5. Walker, J.2008. Fisika. Edisi ke -4.Addison Wesley. 610-630