Disebut Jumlah yang signifikan dengan jumlah digit yang berisi Mantisa dari angka. Semakin banyak angka jumlah yang diketahui dengan ketepatan terbesar. Sebagai pengingat, mantisa adalah angka yang menyertai kekuatan 10 ketika angka dalam notasi ilmiah ditulis.

Misalnya, mari kita ambil nomor 0.00376, yang ditulis sebagai 3.76 x 10 ^-3. Mantisa adalah 3.76 dan jumlahnya memiliki total 3 angka signifikan. Angka 0.129 juga memiliki 3 angka signifikan, sedangkan 4.5 hanya memiliki 2.

Gambar 1. Kalkulator ilmiah tidak pernah menunjukkan jumlah angka signifikan dari suatu operasi. Sumber: Piqsels.

Dan apa yang terjadi saat angkanya utuh? Ini berarti bahwa itu diketahui dengan semua presisi yang mungkin, dengan kata lain, ia memiliki ketepatan yang tak terbatas. Misalnya, dengan menghitung orang, hewan atau benda seperti buku dan telepon, hasilnya adalah bilangan bulat dan bilangan.

Jika kita mengatakan bahwa di bioskop ada 110 orang yang menonton film, ini adalah angka pastinya, tidak lebih atau kurang, dan memiliki 3 angka signifikan.

Angka penting ditangani oleh beberapa aturan sederhana yang dihafal dengan sedikit latihan, seperti yang akan kita lihat saat itu.

[TOC]

Aturan untuk menentukan angka signifikan dari angka

Aturan 1

Nol sebelumnya tidak dihitung sebagai sosok yang signifikan, jadi 0.045 dan 4.5 Mereka memiliki kedua 2 angka signifikan, karena ini mulai dihitung dari kiri dan mulai dari angka nol yang berbeda.

Aturan 2

Zeros posterior (di sebelah kanan) ke digit signifikan pertama dihitung sebagai angka yang signifikan (selama itu dibenarkan oleh keakuratan instrumen pengukuran).

Akhirnya, nol yang berada di tengah juga dihitung sebagai digit yang signifikan.

Aturan 3

Untuk angka yang ditulis dalam notasi ilmiah, semua angka mantisa signifikan, dan eksponen tidak mempengaruhi presisi.

Itu dapat melayani Anda: kecepatan rata -rata: formula, bagaimana itu dihitung dan dipecahkan

Aturan 4

Ketika operasi dengan desimal dilakukan, misalnya dengan menghitung area atau operasi serupa lainnya, hasilnya harus memiliki jumlah angka signifikan yang sama dengan jumlah dengan jumlah rendah dari angka signifikan yang berpartisipasi dalam operasi. Aturan ini berlaku untuk operasi aritmatika apa pun.

Aturan 5

Jumlah jumlahnya tidak mempengaruhi jumlah angka signifikannya.

Kami akan segera melihat beberapa contoh ini dan semua aturan lainnya.

Contoh

Contoh 1

Temukan berapa banyak angka penting yang ada di masing -masing angka ini.

a) 876

b) 1000.68

c) 0.00005026

D) 4.8

e) -6.99

Jawaban

a) 876 memiliki 3 angka signifikan.

b) 1000.68 memiliki 6 angka yang signifikan, karena nol dalam jumlah tengah seperti itu.

c) sebagai gantinya 0.00005026 memiliki 4 angka signifikan. Perhatikan bahwa 5 nol di sebelah kiri 5 tidak dihitung sebagai angka yang signifikan, sebaliknya pada 0 antara 5 dan 2 ya.

D) 4.8 memiliki 2 angka yang signifikan.

e) -6.99 memiliki 3 angka yang signifikan.

Contoh 2

Adalah umum untuk mengambil langkah -langkah langkah, seperti kaset metrik, jam tangan, termometer, timbangan dan sebagainya. Berapa banyak angka penting yang harus kami laporkan jumlah yang kami ukur dengan cara ini?

Menjawab

Itu tergantung pada apresiasi instrumen yang diukur. Mari beri contoh: Ukur diameter eksternal tabung, dengan aturan lulus dan dengan Vernier atau King's Foot.

Vernier adalah instrumen yang mengukur panjangnya dengan sangat tepat karena memiliki skala ekstra kecil, disebut Vernier, yang memungkinkan kehalusan yang lebih besar, untuk berbicara, saat mengukur.

Ini lebih tepat daripada aturan yang lulus karena dengan itu kita dapat mempelajari lebih banyak angka yang lebih signifikan dengan panjang tertentu.

Itulah mengapa tidak masuk akal untuk melaporkan perimeter, katakanlah, 35.88 cm Jika kita mengukurnya dengan pita pengukur, karena instrumen ini tidak cukup tepat untuk melaporkan begitu banyak digit yang signifikan.

Dapat melayani Anda: statis: sejarah, studi apa, aplikasi, hukum

Apresiasi dari pita pengukur diberikan oleh:

Untuk pita pengukur atau aturan milimeter, a = 1 mm, yang merupakan sepersepuluh sentimeter. Perimeter yang diukur dengan pita pengukur harus dilaporkan sebagai 35.9 cm.

Contoh 3

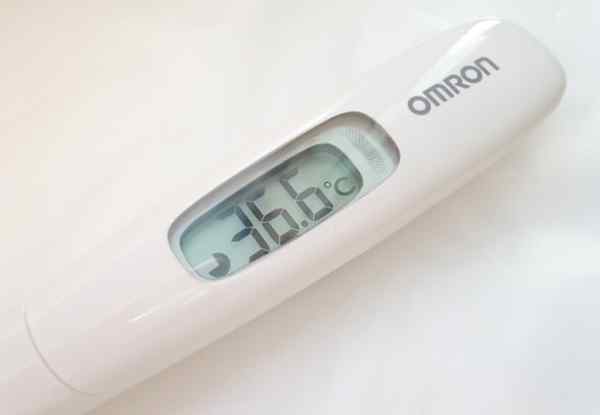
Berapa banyak tokoh penting yang dibaca dengan termometer digital?

Menjawab

Termometer gambar menawarkan pembacaan suhu dengan tiga digit. Namun, sejauh yang ditunjukkan, 36.6 ºC, hanya dua digit pertama dari kiri ke kanan yang tepat, karena desimal dipengaruhi oleh kesalahan apresiasi instrumen, yang biasanya ditunjukkan di belakang yang sama atau dalam manual operasinya.

Hal biasa untuk jenis instrumen digital yang ditampilkan adalah kesalahan 0 apresiasi.1 ºC. Ini cukup untuk memastikan bahwa tidak ada demam.

Gambar 2. Termometer digital yang pembacaannya adalah 3 angka penting. Sumber: Pxhere.

Aturan untuk bundar angka

Ketika kalkulator digunakan untuk melakukan perhitungan dengan langkah -langkah yang diperoleh, tidak benar untuk memberikan hasilnya menggunakan semua angka yang muncul di layar.

Hanya mereka yang mengenal satu sama lain dengan tepat dipertahankan, karena hanya mereka yang memiliki arti sebenarnya. Maka perlu untuk membulatkan hasil agar sesuai dengan jumlah angka yang diketahui secara tepat. Aturan ini adalah:

-Jika nomor yang mengikuti digit yang akan dipertahankan sama dengan atau lebih besar dari 5, Ke digit ini ditambahkan 1.

Misalnya, dengan membulatkan 3.786 untuk memiliki dua desimal, kami ingin mempertahankan angka sampai 8. Karena angka yang mengikuti (6) lebih besar dari 5, 8 menjadi 8 + 1 = 9 dan jumlahnya tetap 3.79.

-Saat angka mengikuti digit yang akan dipertahankan kurang dari 5, Digitnya sama.

Dapat melayani Anda: Efek Joule: Penjelasan, Contoh, Latihan, Aplikasi

Jika kita ingin putaran 1.27924 hanya memiliki 3 desimal, ini dicapai dengan mencapai 9, yang diikuti oleh 2. Karena 2 kurang dari 5, desimal ini menghilang dan bilangan bulat adalah 1.279.

Olahraga diselesaikan

Meja makan memiliki bentuk dan dimensi yang ditunjukkan pada gambar yang terpasang. Itu diminta untuk menghitung luasnya menggunakan aturan operasi dengan angka yang signifikan.

Larutan

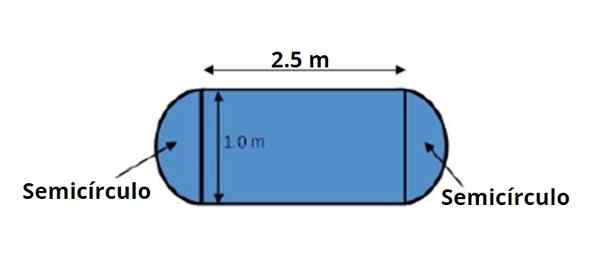Gambar 3. Tabel memiliki bentuk dan dimensi yang ditunjukkan pada gambar, perhatikan bahwa ini diketahui dengan dua angka signifikan. Sumber: f. Zapata.

Area meja dapat dibagi menjadi area persegi panjang pusat dan dua setengah lingkaran, satu di setiap sisi, yang bersama -sama membuat 1 lingkaran penuh.

Kami akan menelepon₁ ke area persegi panjang, diberikan oleh:

KE₁ = basis × tinggi = 2.5 m x 1.0 m = 2.5m²

Untuk bagiannya, area lingkaran, yang setara dengan 1 setengah lingkaran dikalikan dengan 2 adalah:

KE₂ = π × radio²

Diameter dari salah satu lingkaran adalah 1.0 m, oleh karena itu jari -jari itu 0.50 m. Diameter juga dapat digunakan secara langsung untuk menghitung area, dalam hal ini:

KE₂ = (π × diameter²) / 4

Bagaimanapun:

KE₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Semua digit yang ditawarkan oleh kalkulator digunakan. Sekarang kami menambahkan ke₁ sudah₂ Untuk total luas tabel:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Karena dimensi tabel diketahui dengan 2 angka signifikan, tidak masuk akal untuk mengekspresikan hasilnya dengan semua desimal yang diberikan oleh kalkulator, yang tidak pernah memberikan jumlah angka signifikan dari hasil.

Apa yang perlu dilakukan adalah mengitari area tersebut sehingga memiliki jumlah angka signifikan yang sama dengan dimensi tabel, yaitu, 2. Oleh karena itu hasil akhirnya dilaporkan seperti ini:

A = 3.3 m²

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
3. Fisicalab. Angka dan pembulatan yang signifikan. Pulih dari: fisicalab.com.
4. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume1.