Cara mendapatkan sudut segitiga? (Contoh)

Ada berbagai cara Hitung sisi dan sudut segitiga. Ini tergantung pada jenis segitiga yang Anda kerjakan.

Pada kesempatan ini, akan ditunjukkan cara menghitung sisi dan sudut segitiga siku -siku, dengan asumsi bahwa data segitiga tertentu dengan kenalan dengan kenalan.

Elemen yang akan digunakan adalah:

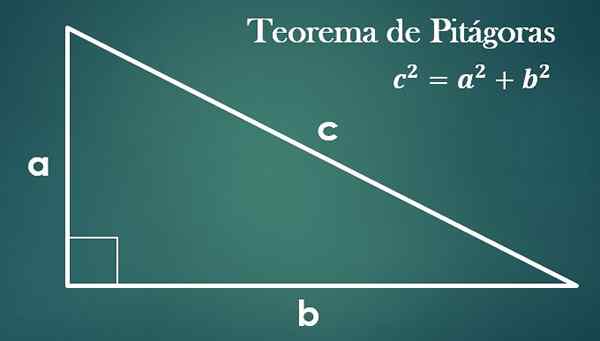
- teorema Pythagoras

Diberi segitiga persegi panjang dengan "A", "B" dan Hypotenusa "C", memang benar bahwa "C² = A²+B²".

- Area segitiga

Rumus untuk menghitung luas segitiga adalah a = (b × h)/2, di mana "b" adalah panjang alas dan "h" panjangnya tinggi.

- Sudut segitiga

Jumlah dari tiga sudut internal segitiga adalah 180 °.

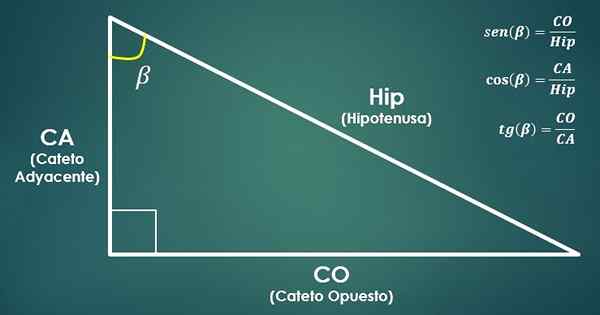
- Fungsi trigonometri:

Pertimbangkan segitiga kanan. Kemudian, fungsi trigonometri didefinisikan sinus, cosinus dan garis singgung sudut beta (β) sebagai berikut:

sin (β) = co/hyp, cos (β) = ca/hip dan tan (β) = co/ca.

Cara menghitung sisi dan sudut segitiga siku -siku?

Diberikan segitiga persegi panjang ABC, situasi berikut dapat disajikan:

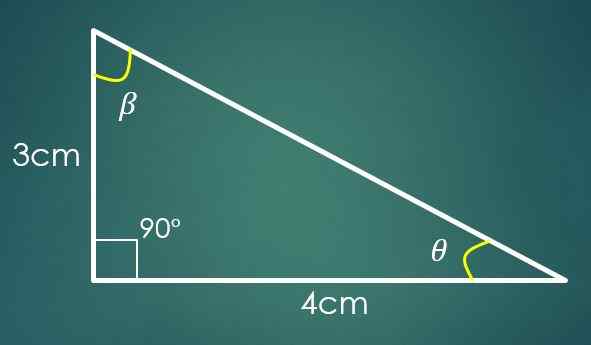
1- Dua kaki diketahui

Jika cateto "A" mengukur 3 cm dan cateto "b" mengukur 4 cm, maka untuk menghitung nilai "C" teorema Pythagoras digunakan. Dengan mengganti nilai "a" dan "b" diperoleh bahwa c² = 25 cm², yang menyiratkan bahwa c = 5 cm.

Sekarang, jika sudut β berlawanan dengan kategori "B", maka sin (β) = 4/5. Saat menerapkan fungsi sebaliknya payudara, dalam kesetaraan terakhir ini diperoleh bahwa β = 53,13º. Dua sudut internal segitiga sudah diketahui.

Misalkan θ menjadi sudut yang masih harus diketahui, lalu 90º+53.13º+θ = 180 °, di mana diperoleh bahwa θ = 36.87º.

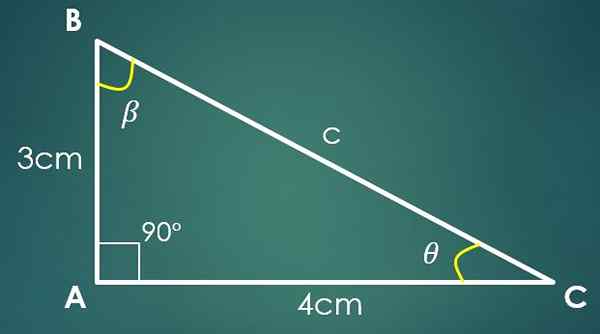
Dalam hal ini tidak perlu bagi sisi yang diketahui menjadi dua kaki, yang penting adalah mengetahui nilai dari kedua sisi mana pun.

2- kaki dan area ini diketahui

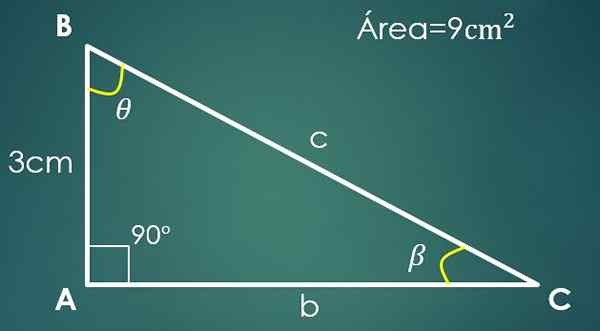
Biarkan a = 3 cm kaki yang diketahui dan 9 cm² area segitiga.

Dalam segitiga persegi panjang, kategori dapat dianggap sebagai alas dan yang lainnya sebagai tinggi (karena mereka tegak lurus).

Misalkan "A" adalah basis, oleh karena itu, 9 = (3 × jam)/2, di mana diperoleh bahwa kategori lainnya berukuran 6 cm. Untuk menghitung hipotenus, lanjutkan seperti pada kasus sebelumnya, dan diperoleh bahwa c = √45 cm.

Sekarang, jika sudut β berlawanan dengan cateto "a", maka sin (β) = 3/√45. Saat membersihkan β diperoleh bahwa nilainya adalah 26,57º. Anda hanya perlu mengetahui nilai sudut ketiga θ.

Dipenuhi bahwa 90 °+26.57º+θ = 180 °, di mana disimpulkan bahwa θ = 63.43º.

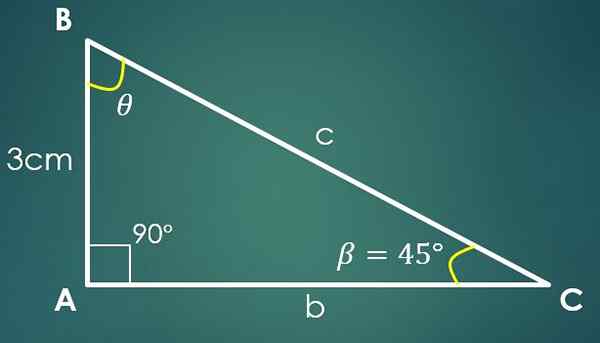
3- sudut dan cateto diketahui

Biarkan β = 45 ° sudut yang diketahui dan A = 3 cm kaki yang diketahui, di mana cateto "a" bertentangan dengan sudut β. Menggunakan rumus garis singgung, diperoleh bahwa Tg (45 °) = 3/Ca, di mana ternyata Ca = 3 cm.

Menggunakan teorema Pythagoras, diperoleh bahwa C² = 18 cm², yaitu, C = 3√2 cm.

Diketahui bahwa sudut berukuran 90 ° dan β berukuran 45 °, dari sini disimpulkan bahwa sudut ketiga berukuran 45 °.

Dalam hal ini, sisi yang diketahui tidak harus menjadi kaki, itu bisa menjadi salah satu dari tiga sisi segitiga.