Bagaimana mendapatkan persentasenya? Contoh dan latihan

Bisa Dapatkan persentase Dengan beberapa metode. Anda dapat dengan cepat menghitung 10% dari angka apa pun hanya saat memindahkan koma desimal Anda posisi ke kiri. Misalnya, 10% dari 100 adalah 10; 10% dari 1000 adalah 100.

Jika Anda ingin menghitung persentase yang lebih kompleks seperti 36% dari 25 atau 250% dari 20, metode lain diperlukan. Untuk kasus di mana sistem 10% tidak berlaku, metodologi berikut dapat diperhitungkan.

Gambar 1. Diskon dengan persentase yang berbeda. Berapa banyak kita saling menyelamatkan?. Sumber: Pixabay.

Istilah persentase berarti bagian tertentu dari setiap seratus dan merujuk pada operasi aritmatika yang dilakukan untuk menemukan bagian tersebut. Misalnya 20% ("dua puluh persen") dibaca dalam peso, itu berarti bahwa 20 peso didiskon untuk setiap 100 peso.

Persentase berfungsi untuk menghitung bagian mana dari total yang mewakili jumlah. Dalam hal ini, total diambil pada skala 100 dan persentase menginformasikan berapa banyak, berdasarkan pada 100, adalah bagian yang akan dihitung.

Mari kita lihat bagaimana hal itu dilakukan dengan contoh -contoh ini. Pertama -tama kita melakukannya dalam bentuk fraksi:

• 20% = 20/100
• 5% = 5/100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Perhatikan bahwa 100% sama dengan 1. Tetapi persentasenya juga dapat ditulis desimal:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1.0

Ketika persentase dari angka tertentu diungkapkan, sederhana Koma bergerak Dari tempat itu nomor dua di sebelah kiri. Dalam persentase, Aturan proporsionalitas:

20% adalah 20 dari 100, oleh karena itu:

20% dari 100 adalah 20, 20% dari 200 adalah 40, 20% dari 300 adalah 60, 20% dari 50 adalah 10.

Aturan umum untuk 20 % dari jumlah berapa pun

20% dari x adalah x *(20/100) = x *0,2 = 0,2 *x

Aturan ini dapat dengan mudah diperluas untuk menemukan persentase lain yang diinginkan. Mari kita lihat bagaimana di bagian berikut.

Latihan diselesaikan dengan formula untuk menghitung n% 

Formula untuk diringkas sesegera mungkin dan dengan cepat menghitung persentase apa pun N adalah:

N % =(A * n)/100

Misalnya Anda ingin menghitung 25% dari 400

Kemudian n = 25 dan A = 400, menghasilkan (400*25)/100 = 100

Contoh

Berapa persentase 60 adalah 24?

Larutan

Apa yang diminta setara dengan menanyakan apa N% dari 60 yang memberi 24?

Kami mengusulkan formula umum:

60 * n / 100 = 24

Kami jelas N Dengan prosedur ini:

-100 yang membagi menjadi anggota iZiédo Kesetaraan, pergi ke anggota Kanan mengalikan. 

-Dan 60 yang berlipat ganda dalam anggota kiri Pergi ke anggota Kanan pemisah.

N = 24 *100 /60 = 2400 /60 = 240/6 = 6 *40 /6 = 40

Disimpulkan bahwa 40% dari 60 adalah 24.

Latihan Perhitungan Persentase Terpecahkan 

Di bawah ini adalah latihan sederhana untuk mulai mempraktikkan yang disebutkan di atas.

Itu dapat melayani Anda: 15 legenda dan mitos paling populer

Latihan 1

Temukan 50% dari 90.

Larutan

Di sini x = 90, n = 50 % dan ganti:

90 * 50% = 90 * (50 /100) = 4500 /100 = 45 

Ini cukup sederhana, karena 50 % dari jumlah berapa pun adalah setengah dari jumlah itu dan setengah dari 90 adalah 45.

Latihan 2

Temukan 30% dari 90.

Larutan

90 * 30% = 90 * (30 /100) = 2700 /100 = 27

Persentase meningkat

Sering dalam kehidupan sehari -hari untuk mendengarkan peningkatan sesuatu, misalnya peningkatan produksi, kenaikan gaji atau kenaikan produk. Hampir selalu diungkapkan dalam bentuk persentase.

Misalnya, biaya produk tertentu € 300 tetapi mengalami peningkatan 30%. Kami bertanya pada diri sendiri: berapa harga produk baru?

Yang pertama adalah menghitung porsi yang sesuai dengan peningkatan. Karena kenaikannya adalah 30 bagian dari 100, maka peningkatan kenaikan, berdasarkan harga asli 300, adalah tiga kali 30 bagian, yaitu 3*30 = 90.

Produk meningkat € 90, jadi harga akhir yang baru akan menjadi biaya kenaikan sebelumnya:

Harga baru = harga lama + € 90 = € 390

Kita dapat membangun formula untuk perhitungan peningkatan persentase. Kami menggunakan huruf untuk melambangkan harga, seperti ini:

-F adalah nilai akhir

-yo adalah nilai awal dan

-N adalah peningkatan peningkatan.

Dengan nama -nama ini, nilai akhir akan dihitung seperti ini:

f = i + (i* n / 100)

tapi bagaimana caranya yo Diulangi dalam kedua istilah, itu dapat dianggap sebagai faktor umumUntuk mendapatkan ekspresi lain ini, sama validnya:

F = i * (1 + n / 100)

Mari kita verifikasi dengan kasus yang sudah diselesaikan, produk yang harganya € 300 dan meningkat 30%. Dengan demikian kami memastikan bahwa formula bekerja dengan baik:

Harga akhir = F = € 300 * (1 + 30/100) = € 300 * (1 + 0.3) = € 300 * 1.3 = € 390

Latihan 3

Seorang karyawan memperoleh € 1500, tetapi dipromosikan dan gajinya memiliki kenaikan 20%. Berapa gaji baru Anda?

Larutan

Mari terapkan formula:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0.2) = € 1500 * 1.2 = € 1800

Gaji karyawan baru adalah € 1800.

Persentase berkurang

Dalam kasus penurunan, rumus untuk perhitungan nilai akhir F dari jumlah awal tertentu yo yang mengalami penurunan N% adalah:

F = i * (1 - n / 100)

Perlu dicatat bahwa tanda positif (+) dari rumus di bagian sebelumnya digantikan oleh tanda negatif (-).

Gambar 2. Persentase Pemberitahuan Diskon. Sumber: Pixabay

Latihan 4

Produk ditandai € 800, tetapi menerima diskon 15%. Berapa harga produk baru?

Solusi 4

Harga akhir menurut formulanya adalah:

F = € 800 * (1 - 15/100) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

Harga akhir dengan diskon 15% adalah € 680, yang mewakili penghematan € 120.

Persentase berturut -turut

Tampaknya ketika beberapa jumlah mengalami variasi persentase dan kemudian yang lain diterapkan, juga persentase. Misalnya produk yang memiliki dua diskon persentase berturut -turut. Contoh lain adalah seorang karyawan yang memiliki dua kenaikan gaji berturut -turut.

Dapat melayani Anda: kegiatan ekonomi yucatan yang lebih penting

- Persentase berturut -turut meningkat

Basis solusi dari kasus -kasus ini sama dengan peningkatan yang unik, tetapi harus diperhitungkan bahwa peningkatan persentase kedua dilakukan pada nilai akhir dari peningkatan pertama.

Misalkan produk yang naik 10% pertama dan kemudian 5%. Tidak benar untuk mengatakan bahwa ia mengalami peningkatan 15%, sebenarnya lebih dari persentase ini.

Rumus untuk nilai akhir akan berlaku seperti ini:

-Pertama nilai akhir dari peningkatan pertama N1% dihitung

f1 = i + i * n1 / 100

-Dan kemudian, untuk menemukan nilai akhir dari peningkatan kedua N2%, nilai akhir F1 diambil sebagai nilai awal. Karena itu:

F2 = f1 + f1 * n2 /100 

Latihan 5

Sebuah buku awalnya berharga € 55, tetapi karena keberhasilan dan permintaannya yang tinggi, ia menderita dua kenaikan berturut -turut pada harga aslinya. Peningkatan pertama adalah 10% dan yang kedua dari 20%. Berapa harga akhir buku ini?

Larutan

-Peningkatan pertama:

F1 = € 55 * (1 + 10/100) = € 55 * 1.1 = € 60.5

-Kenaikan kedua

F2 = € 60.5 * (1 + 20/100) = € 60.5 * 1.2 = € 72.6

Harga akhir adalah € 72.6.

Latihan 6

Mengacu pada latihan sebelumnya. Dua kenaikan berturut -turut: berapa persentase kenaikan unik dari harga buku asli yang sesuai?

Larutan

Jika kita memanggil N% ke persentase peningkatan unik, formula yang menghubungkan persentase unik ini kenaikan nilai aslinya dan nilai akhirnya adalah:

F2 = i *(1 + n / 100) 

Artinya:

€ 72,6 = € 55 + 55 € * (n / 100)

Membersihkan peningkatan peningkatan n% = (n /100), kami memiliki:

(N / 100) = (€ 72,6 - € 55) / 55 € = 17.€ 6 / € 55 = 0,32

Karena itu:

N = 0,32 * 100 = 32

Dengan harga buku kenaikan persentase total 32% diterapkan. Perhatikan bahwa peningkatan ini lebih besar dari jumlah peningkatan persentase berturut -turut.

- Diskon persentase berturut -turut

Idenya mirip dengan persentase berturut -turut meningkat. Diskon persentase kedua harus selalu diterapkan pada nilai akhir dari diskon pertama, mari kita lihat contoh:

Latihan 7

Diskon 10% diikuti dengan diskon kedua 20% pada suatu objek, di mana diskon persentase unik itu setara?

Larutan

-Diskon pertama:

F1 = i - i * n1 / 100  

-Diskon kedua

F2 = f1 - f1 * n2 / 100

Mengganti persamaan pertama di yang kedua tetap:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Mengembangkan ungkapan ini, kami dapatkan:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Menggambar faktor umum yo:

F2 = I * (1- N1% - N2% + N1% * N2%)

Akhirnya, persentase yang ditunjukkan dalam pertanyaan diganti:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100 /100) = i * (1 - 28%)

Dengan kata lain, diskon berturut -turut 10% dan 20% sesuai dengan diskon 28% yang unik.

Latihan lanjutan

Mari kita coba latihan ini hanya ketika ide -ide yang sebelumnya cukup jelas.

Itu dapat melayani Anda: sampul geografi yang mudah dan indah, sampul, gambar

Latihan 8

Dasar segitiga berukuran 10 cm dan tinggi 6 cm. Jika panjang dasar berkurang 10%. Dalam berapa persentase harus ditingkatkan sehingga area segitiga tidak berubah?

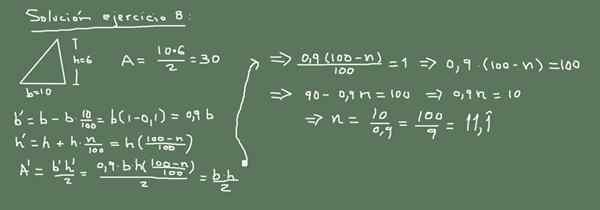Gambar 3. Solusi alternatif untuk Latihan 8. Disiapkan oleh f. Zapata.

Solusi 8

Area segitiga asli adalah:

A = (10cm * 6cm) / 2 = 30 cm²

Sekarang, jika basis berkurang 10%, maka nilainya baru adalah:

Basis baru = 10 - (10/100) x 10 = 9 cm.

Nilai tinggi baru adalah x, dan area aslinya harus dijaga tidak berubah, sehingga:

(9cm * x) /2 = 30 cm²

Maka nilai x dibersihkan sebagai:

X = 60 cm² / 9 cm = (20/3) cm = 6.666 cm

Yang berarti peningkatan 0,666 dibandingkan dengan nilai aslinya. Mari kita lihat sekarang berapa persentase dari ini:

6.666 = 6 + (6 * n/100) 

6.666 -6 = 6 * n/100

0.666 = 6 * n/100

N/100 = 0,111

N = 11.1

Jawabannya adalah: ketinggian harus ditingkatkan sebesar 11,1% agar area segitiga tetap sama.

Latihan 9

Jika gaji meningkat sebesar 20%, tetapi kemudian pajak diskon 5%, apa kenaikan sebenarnya yang diterima pekerja?

Larutan 

Pertama kami menghitung peningkatan N1%:

f1 = i + i * n1 / 100

Kemudian kami menerapkan diskon N2%:

F2 = f1 - f1 * n2 / 100

Persamaan pertama diganti di yang kedua:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Ekspresi sebelumnya berkembang:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Akhirnya dihapus yo Faktor Umum dan Nilai N1 = 20 dan N2 = 5 yang muncul dalam pernyataan diganti:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Pekerja menerima kenaikan bersih 14%.

Latihan 10

Putuskan apa yang paling nyaman di antara kedua opsi ini:

i) memperoleh T -shirts dengan diskon 32 % masing -masing.

Ii) Beli 3 T -Rhirts dengan harga 2.

Larutan 

Kami menganalisis setiap opsi secara terpisah dan kemudian memilih yang paling ekonomis:

i) Misalkan X menjadi harga kemeja saat ini, diskon 32 % mewakili harga akhir xf:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Misalnya, membeli 3 kemeja berarti menghabiskan 3 x 0.68 x = 2.04x

ii) Jika x adalah harga kemeja, untuk 3 kemeja Anda hanya akan membayar 2x.

Misalkan kemeja bernilai 6 euro, dengan diskon 32 % akan bernilai 4.08 Euro. Beli 1 T -Pelang bukanlah opsi yang valid dalam penawaran 3 × 2. Jadi jika Anda hanya ingin membeli 1 kemeja, diskon lebih disukai.

Tetapi jika yang Anda inginkan adalah membeli untuk lusinan, penawaran 3 × 2 hanya sedikit lebih murah. Misalnya, 6 T -Rhirts dengan diskon akan keluar untuk 24.48 Euro, sedangkan dengan penawaran 3 × 2 mereka akan menelan biaya 24 euro

Referensi

1. Ruang kelas yang mudah. Persentase. Diperoleh dari: ruang kelas.com
2. Baldor a. 2006. Aritmatika teoretis praktis. Edisi Budaya.
3. Educa Kids. Bagaimana belajar menghitung persentase. Dipulihkan dari: Educapequees.com
4. Gutiérrez, g. Catatan Matematika Keuangan. Pulih dari: csh.Izt.Uam.MX
5. Kutu Cerdas. Persentase: Apa itu dan bagaimana dihitung. Pulih dari: smartick.adalah