Sistem Koordinat Silindris, Perubahan dan Latihan

Itu Koordinat silinder Mereka berfungsi untuk menemukan titik dalam ruang tiga dimensi dan terdiri dari koordinat radial ρ, koordinat azimutal φ dan koordinat tinggi z.

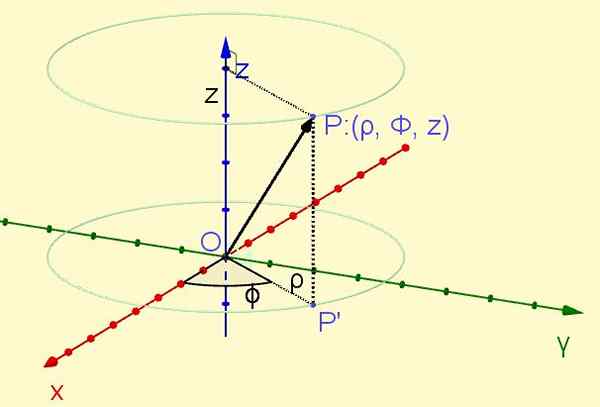
Sebuah titik P Terletak di luar angkasa diproyeksikan secara ortogonal di pesawat Xy memunculkan intinya P ' Di pesawat itu. Jarak dari asal ke titik P ' mendefinisikan koordinat ρ, sedangkan sudut yang membentuk sumbu X Dengan semi -mudah Op ' Tentukan koordinat φ. Akhirnya, koordinat z Itu adalah proyeksi ortogonal dari poin P pada poros Z. (Lihat Gambar 1).

Gambar 1. Titik P dari koordinat silinder (ρ, φ, z). (Elaborasi sendiri)

Koordinat radial ρ selalu positif, koordinat azimutal φ bervariasi dari nol radian hingga dua pi radianes, sedangkan koordinat z dapat mengambil nilai nyata:

0 ≤ ρ < ∞

0 ≤ φ < 2π

- ∞ < z < + ∞

[TOC]

Perubahan Koordinat

Relatif mudah untuk mendapatkan koordinat cartesian (x, y, z) dari titik p dari koordinat silindernya (ρ, φ, z):

x = ρ cos (φ)

y = ρ sen (φ)

z = z

Tetapi juga dimungkinkan untuk mendapatkan koordinat kutub (ρ, φ, z) berdasarkan pengetahuan koordinat cartesian (x, y, z) dari titik p:

ρ = √ (x² + Dan²)

φ = arctan (y/x)

z = z

Basis vektor dalam koordinat silinder

Basis vektor silinder didefinisikan Uρ, Uφ, Uz.

Vektor Uρ Itu bersinggungan dengan garis φ = ctte dan z = ctte (menunjuk secara radial keluar), vektor Uφ bersinggungan dengan garis ρ = ctte dan z = ctte dan akhirnya Uz Ini memiliki arah yang sama dari sumbu z.

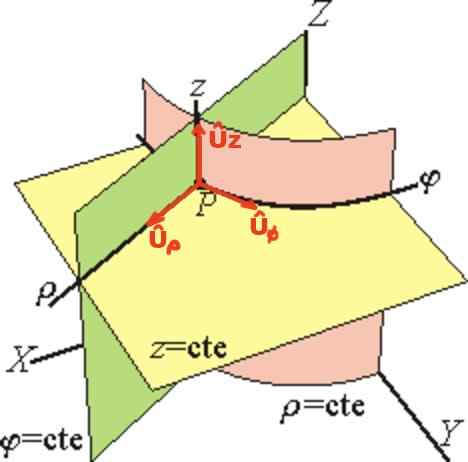Gambar 2. Basis koordinat silinder. (Wikimedia Commons)

Di basis unit silindris, vektor posisi R Dari titik p itu ditulis secara vektor seperti ini:

Itu dapat melayani Anda: domain dan kontradiksi suatu fungsi (dengan contoh)

R = ρ Uρ + 0 Uφ + z Uz

Di sisi lain, perpindahan yang sangat kecil dR Dari titik P itu dinyatakan sebagai berikut:

DR = Dρ Uρ + ρ dφ  Uφ + Dz Uz

Demikian pula, elemen volume DV yang sangat kecil dalam koordinat silinder adalah:

Dv = ρ dρ dφ dz

Contoh

Ada banyak contoh penggunaan dan penerapan koordinat silinder. Dalam kartografi, misalnya, Proyeksi silinder, berdasarkan koordinat ini. Ada lebih banyak contoh:

Contoh 1

Koordinat silindris memiliki aplikasi dalam teknologi. Sebagai contoh, Anda memiliki sistem Lokasi Data CHS (Sektor Kepala Silinder) pada hard drive, yang sebenarnya terdiri dari beberapa disk:

- Silinder atau trek sesuai dengan koordinat ρ.

- Sektor ini sesuai dengan posisi φ dari album yang berputar di atas Kecepatan sudut.

- Kepala sesuai dengan posisi z dari kepala baca di album yang sesuai.

Setiap byte informasi memiliki alamat yang tepat dalam koordinat silinder (C, S, H).

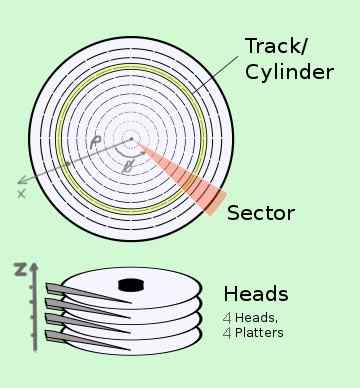Gambar 2. Lokasi Informasi dalam Koordinat Silindris dalam Sistem Hard Drive. (Wikimedia Commons)

Contoh 2

Derek konstruksi mengatur posisi beban dalam koordinat silinder. Posisi horizontal ditentukan oleh jarak ke sumbu atau panah derek. Posisi vertikal beban ditentukan oleh koordinat Z ketinggian.

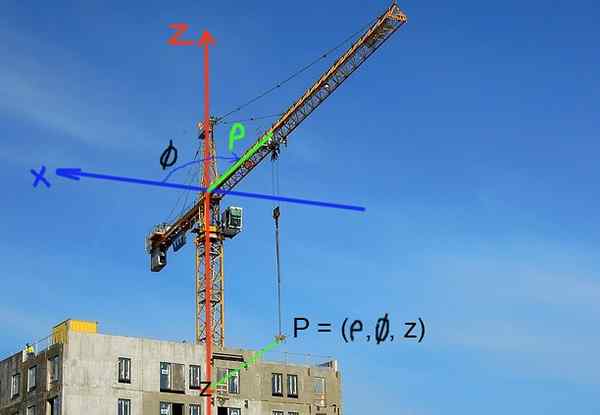Gambar 3. Posisi beban dalam derek konstruksi dapat dengan mudah diekspresikan dalam koordinat silinder. (Gambar Pixabay - RCOS R. Pérez)

Latihan terpecahkan

Latihan 1

Ada titik P1 dari koordinat silinder (3, 120º, -4) dan titik P2 dari koordinat silinder (2, 90º, 5). Temukan Jarak Euclidian Di antara dua poin ini.

Dapat melayani Anda: divisi di mana residu 300

Larutan: Pertama, kami melanjutkan untuk menemukan koordinat cartesian dari setiap titik mengikuti formula yang terjadi di atas.

P1 = (3* cos 120º, 3* sen 120º, -4) = (-1.5, 2.60, -4)

P2 = (2* cos 90º, 2* sin 90º, 5) = (0, 2, 5)

Jarak Euclidian antara P1 dan P2 adalah:

D (P1, P2) = √ ((0 - (-1.5))²+(2 - 2.60)²+(5 -(-4))² ) = ..

… √ (2.25+0.36+81) = 9.14

Latihan 2

Poin P memiliki koordinat cartesian (-3, 4, 2). Temukan koordinat silinder yang sesuai.

Larutan: Koordinat silinder ditemukan menggunakan hubungan yang diberikan di atas:

ρ = √ (x² + Dan²) = √ ((-3)² + 4²) = √ (9 + 16) = √ (25) = 5

φ = arctan (y/x) = arcan (4/(-3)) = -53.13º + 180º = 126.87º

Z = 2

Perlu diingat bahwa fungsi yang bergantung adalah multivaluada dari periodisitas 180º. Selain itu, sudut φ harus menjadi milik kuadran kedua, karena koordinat x e y dan titik p berada di kuadran itu. Inilah alasan mengapa 180º telah ditambahkan ke hasil φ.

Latihan 3

Ekspresikan dalam koordinat silinder dan dalam koordinat cartesian permukaan silinder radio 2 dan yang sumbu bertepatan dengan sumbu z.

Solusi: Dapat dipahami bahwa silinder memiliki ekstensi tak terbatas dalam arah z, sehingga persamaan permukaan tersebut dalam koordinat silinder adalah:

ρ = 2

Untuk mendapatkan persamaan Cartesian dari permukaan silindris, kuadrat dari kedua anggota persamaan sebelumnya diambil:

ρ² = 4

Kami melipatgandakan dengan 1 anggota kesetaraan sebelumnya dan menerapkan Identitas Trigonometri Dasar (Sen²(φ) + cos²(φ) = 1):

1 * ρ² = 1 * 4

(Sen²(φ) + cos²(φ)) * ρ² = 1 * 4

Tanda kurung berkembang untuk mendapatkan:

(ρ sen (φ))² + (ρ cos (φ))² = 4

Dapat melayani Anda: populasi dan sampel

Kami ingat bahwa tanda kurung pertama (ρ sen (φ)) adalah koordinat dan titik dalam koordinat kutub, sedangkan tanda kurung (ρ cos (φ)) mewakili koordinat x, sehingga kami telah pergi Persamaan silinder dalam koordinat cartesian:

Dan² + X² = 2²

Persamaan sebelumnya tidak boleh disamakan dengan lingkaran di bidang XY, karena dalam hal ini akan seperti ini: dan² + X² = 2² ; Z = 0.

Latihan 4

Silinder jari -jari r = 1 m dan tinggi h = 1m memiliki massa terdistribusi secara radial sesuai dengan persamaan berikut d (ρ) = C (1 - ρ/r) di mana C adalah konstanta nilai c = 1 kg/m/m³. Temukan massa total silinder dalam kilogram.

Larutan: Hal pertama adalah untuk menyadari bahwa fungsi d (ρ) mewakili kepadatan massa volumetrik, dan bahwa massa kepadatan didistribusikan dalam cascarone silinder dengan penurunan kepadatan pusat ke pinggiran. Elemen volume yang sangat kecil menurut simetri masalahnya adalah:

Dv = ρ dρ 2π h

Dari sana Anda harus melakukannya, massa yang sangat kecil dari cangkang silindris adalah:

Dm = d (ρ) dv

Jadi massa total silinder akan diekspresikan dengan yang berikut ini Didefinisikan integral:

M = ∫_{salah satu}^R D (ρ) dv = ∫_{salah satu}^R C (1 - ρ/r) ρ dρ 2π h = 2π h c ∫_{salah satu}^R (1 - ρ/r) ρ dρ

Solusi dari integral yang ditunjukkan tidak sulit diperoleh, sebagai hasilnya:

∫_{salah satu}^R (1 - ρ/r) ρ dρ = (⅙) r²

Memasukkan hasil ini dalam ekspresi massa silinder diperoleh:

M = 2π h c (⅙) r² = ⅓ π h c r² =

 ⅓ π 1m*1kg/m³* 1m² = π/3 kg ≈ 1.05 kg

Referensi

1. Arfken G dan Weber H. (2012). Metode Matematika untuk Fisikawan. Panduan komprehensif. Edisi ke -7. Pers Akademik. ISBN 978-0-12-384654-9
2. Perhitungan CC. Masalah koordinat silinder dan bola terpecahkan. Pulih dari: perhitungan.Dc
3. Weisstein, Eric W. “Koordinat silinder.”Dari MathWorld-A Wolfram Web. Dipulihkan dari: MathWorld.Wolfram.com
4. Wikipedia. Sistem Koordinat Silindris. Diperoleh dari: di.Wikipedia.com
5. Wikipedia. Bidang vektor dalam koordinat silinder dan bola. Diperoleh dari: di.Wikipedia.com