Fungsi dan Aplikasi Trigonometri Lingkaran Kesatuan

Dia Lingkaran Kesatuan Ini adalah lingkaran jari -jari yang sama dengan 1, yang biasanya difokuskan pada titik (0,0) dari sistem koordinat Cartesian Xy. Ini digunakan untuk dengan mudah mendefinisikan alasan trigonometri sudut dengan persegi panjang.

Persamaan lingkaran kesatuan yang difokuskan pada asal adalah:

X² + Dan² = 1

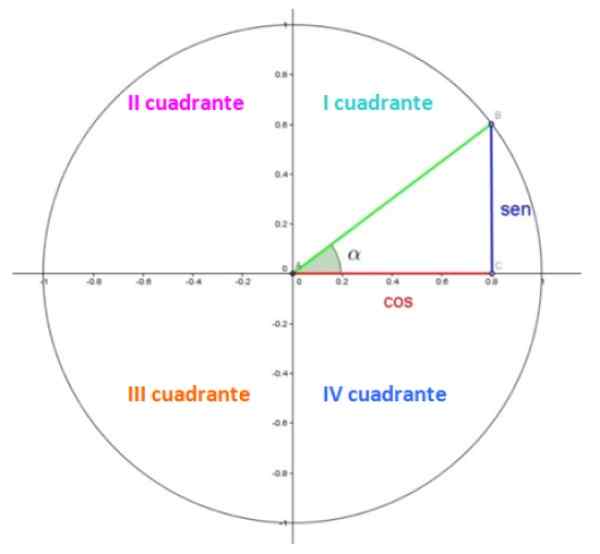
Gambar 1. Lingkaran unit. Sumber: Wikimedia Commons.

Pada Gambar 1 kita memiliki lingkaran unit, di mana setiap kamar berada di kuadran. Kuadran diberi nomor dengan nomor Romawi dan dihitung anti -SHORARY.

Di kuadran pertama ada segitiga. Kategori, masing -masing dalam ukuran merah dan biru 0.8 dan 0.6, sedangkan hipotenus dalam ukuran hijau 1, karena itu adalah radio.

Sudut akut α adalah sudut tengah dalam posisi standar, yang berarti verteksnya bertepatan dengan titik (0,0) dan sisi awalnya dengan sumbu x positif. Sudut diukur bertentangan dengan tangan jam dan dengan konvensi itu diberi tanda positif.

Nah, dalam lingkaran satuan, koordinat coseno dan sinus α masing -masing adalah koordinat x dan y titik B, yang dalam contoh yang ditunjukkan adalah 0.8 dan 0.6.

Dari keduanya mereka didefinisikan:

• TG α = sin α/cos α = 0.6/0.8 = 0.75
• Dt α = 1/ cos α = 1/0.8 = 1.25
• Harm α = 1 / sin α = 1/0.6 = 1.66 ..
• CTG α = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Aplikasi Lingkaran Kesatuan

Jika kita membatasi diri pada persegi panjang, alasan trigonometri hanya akan diterapkan pada sudut akut. Namun, dengan bantuan lingkaran unit, perhitungan alasan trigonometri diperluas ke sudut α apa pun.

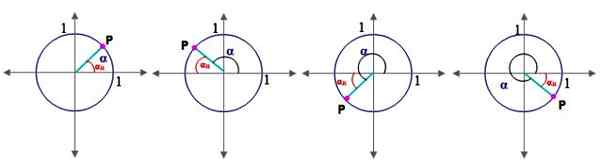
Gambar 2.- Sudut di kuadran dan sudut referensi di lingkaran unit. Sumber: f. Zapata.

Untuk ini, perlu untuk mendefinisikan konsep sudut referensi α terlebih dahulu_R:

Dapat melayani Anda: Himpunan terbatas: properti, contoh, latihan terpecahkan

Sudut referensi

Biarkan α menjadi sudut dalam posisi standar (yang Sisi awal bertepatan dengan sumbu x positif), sudut rujukannya α_R Itu termasuk di antara sisi terminal dan sumbu x. Gambar 2 menunjukkan sudut referensi untuk sudut dalam kuadran I, II, III dan IV.

Untuk setiap kuadran, sudut referensi dihitung sebagai berikut:

-Kuadran Pertama: α_R = α

-Kuadran kedua: α_R = 180º - α

-Kuadran ketiga: α_R = α - 180º

-Kuadran Keempat: α_R = 360º - α

Perhatikan bahwa sudut kuadran pertama α bertepatan dengan sudut rujukannya. Nah, alasan trigonometri untuk sudut α sama dengan sudut referensi mereka, dengan tanda -tanda menurut mereka yang memiliki kuadran di mana sisi terminal α jatuh.

Dengan kata lain, alasan trigonometri coseno dan payudara sudut α bertepatan dengan koordinat titik P, menurut Gambar 2.

Pada gambar berikut kita melihat alasan trigonometri dari beberapa sudut yang terkenal, sebagaimana disimpulkan dari lingkaran unit.

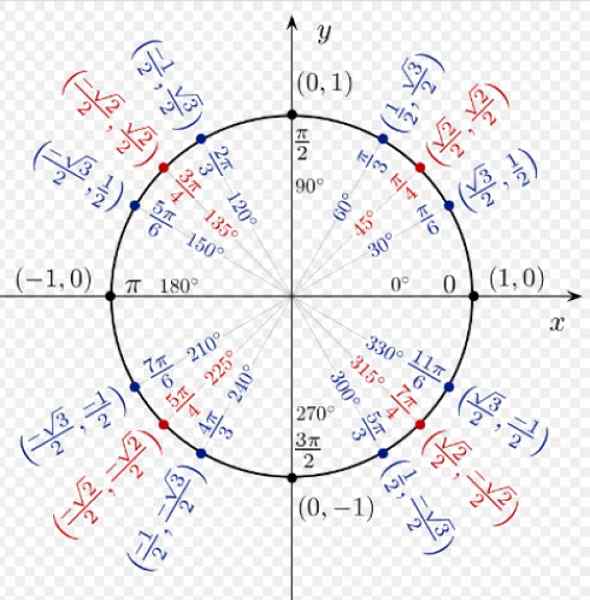Gambar 3. Koordinat beberapa titik penting dalam lingkaran unit. Sumber: Wikimedia Commons.

Alasan coseno dan payudara sudut apa pun di kuadran I semuanya positif. Untuk α = 60º kami memiliki koordinat (1/2; √3/2), yang masing -masing sesuai dengan cos 60º dan sen 60º.

Koordinat α = 120º adalah (-1/2; √3/2), karena berada di kuadran kedua, koordinat x negatif.

Tata letak grafik kosinus dan sinus

Dengan bantuan lingkaran satuan dan koordinat titik P di atasnya, dimungkinkan untuk menggambar grafik fungsi cos t dan sen t, seperti yang akan kita lihat di bawah.

Dapat melayani Anda: perpindahan sudut

Untuk ini, beberapa posisi titik P (t) terletak di lingkaran unit. Kita akan mulai dengan grafik fungsi f (t) = sen t.

Kita dapat mengamati bahwa ketika kita beralih dari t = 0 ke t = π/2 (90º) Nilai sen t meningkat menjadi 1, yang merupakan nilai maksimum.

Di sisi lain, dari t = π/2 hingga t = 3π/2 Nilai sin t berkurang dari 1, melewati 0 pada t = π ke minimum -1 pada t = 3π/2.

Gambar tersebut menunjukkan grafik siklus pertama f (t) = sen yang sesuai dengan pengembalian pertama ke lingkaran unit, fungsi ini periode periodik 2π.

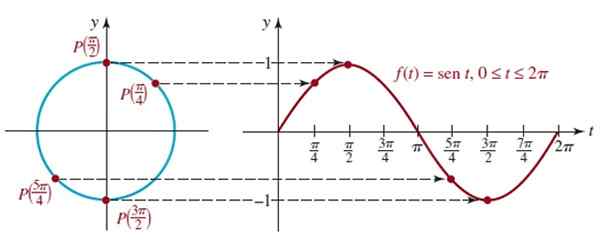Gambar 4. Angka grafik f (t) = sen t untuk siklus. Sumber: Zill, D. Aljabar, trigonometri dan geometri analitik.

Prosedur analog dapat dilakukan untuk mendapatkan grafik fungsi f (t) = cos t, seperti yang ditunjukkan dalam animasi berikut:

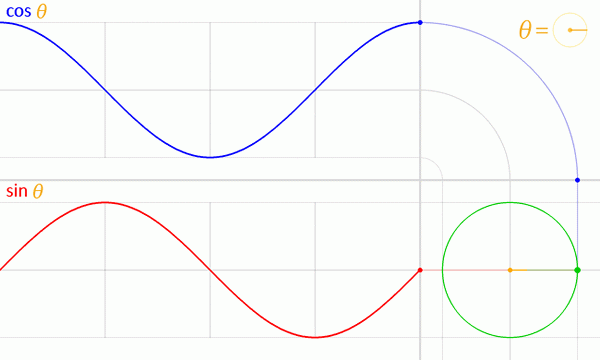Gambar 5. Grafik fungsi sine dan cosinus dari lingkaran unit. Sumber: Wikimedia Commons.

Properti fungsi seno dan coseno

-Kedua fungsi itu kontinu dalam set angka nyata dan juga periodik, periode 2π.

-Domain fungsi f (t) = sen t dan f (t) = cos t semuanya bilangan real: (-∞, ∞).

-Untuk rute payudara atau sinus dan kosinus Anda memiliki interval [-1,1]. Kurung menunjukkan bahwa -1 dan 1 disertakan.

- Dosa T Zeros adalah nilai yang sesuai dengan Nπ dengan n integer, sedangkan nol cos t adalah [(2n+1)/2] dengan n juga keseluruhan.

-Fungsi f (t) = sin t adalah ganjil, memiliki simetri sehubungan dengan asal sedangkan fungsi cos t bahkan, simetrinya sehubungan dengan sumbu vertikal.

Dapat melayani Anda: pilihan acak dengan atau tanpa penggantian

Latihan terpecahkan

- Latihan 1

Diberikan cos t = - 2/5, yang merupakan koordinat horizontal titik p (t) di lingkaran satuan di kuadran kedua, dapatkan koordinat vertikal yang sesuai Sen T.

Larutan

Karena P (t) milik lingkaran satuan, di mana dipenuhi bahwa:

X² + Dan² = 1

Karena itu:

y = ± √ 1 - x²

Karena p (t) berada di kuadran kedua, nilai positif akan diambil. Koordinat vertikal titik p (t) adalah y:

y = √ 1 - (-2/5)² = √0.84

- Latihan 2

Model matematika untuk suhu T Dalam derajat Fahrenheit pada hari apa pun, T Beberapa jam setelah tengah malam, itu diberikan oleh:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

Dengan t dipahami antara 0 dan 24 jam. Menemukan:

a) suhu pada jam 8 pagi.

b) jam di mana t (t) = 60 ºF

c) suhu maksimum dan minimal.

Solusi untuk

Kami mengganti t = 8 dalam fungsi yang diberikan:

T (8) = 50 + 10 sen [(π/12) × (T-8)] = 50 + 10 sen [(π/12) × (8-8)] =

= 50 + 10 x sen 0 = 50 ºF

Solusi b

50 + 10 sen [(π/12) × (T-8)] = 60

Ini adalah persamaan trigonometri dan Anda harus menghapus "T" yang tidak diketahui:

10 sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (T-8)] = 1

Kita tahu bahwa sen π/2 = 1, oleh karena itu argumen payudara harus 1:

(π/12) × (T-8) = π/2

T-8 = 6

t = 14 jam

Disimpulkan bahwa 14 jam setelah tengah malam suhunya 60 °, yaitu, jam 2 siang. Tidak ada jam lain sepanjang hari (24 jam) di mana ini terjadi.

Solusi c

Suhu maksimum sesuai dengan nilai di mana sen [(π/12) × (T-8)] = 1 dan 60 ºF. Di sisi lain, minimum terjadi jika sen [(π/12) × (t -8)] = -1 dan 40 ºF.

Referensi

1. Figuera, J. 1999. Matematika. 1st. Diversifikasi. Edisi Collegiate Bolivarian.
2. Hoffman, J. Pemilihan masalah matematika. Volume 4.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Matematika itu menyenangkan. Lingkaran satuan. Pulih dari: dari: mathsisfun.com.
5. Wikipedia. Identitas dan formula trigonometri. Pulih dari: is.Wikipedia.org.
6. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.