Identitas trigonometri (contoh dan latihan)

Itu Identitas trigonometri Ini adalah hubungan antara alasan trigonometri, yang berlaku untuk nilai variabel apa pun. Misalnya:

Tan θ = sin θ /cos θ

Ini adalah identitas trigonometri yang menghubungkan tiga alasan sudut θ, garis singgung, payudara dan kosinus sudut tersebut.

Gambar 1. Beberapa identitas trigonometri banyak digunakan dalam perhitungan. Sumber: f. Zapata.

Identitas ini berlaku untuk semua nilai, kecuali yang membuat 0 penyebut. Cos θ adalah 0 untuk θ = ± π/2, ± 3π/2, ± 5π/2 ... Contoh lain dari identitas trigonometri adalah:

dosa x . Sec x . CTG X = 1

[TOC]

Demonstrasi

Ada dua cara dasar untuk menunjukkan bahwa identitas trigonometri benar:

1- Mengubah salah satu anggota kesetaraan menjadi yang lain, melalui manipulasi aljabar yang nyaman.

2- Kembangkan kedua anggota kesetaraan secara terpisah, sampai masing-masing ekspresi akhir dari masing-masing sama.

Dalam identitas yang diusulkan, kita akan mengubah sisi kiri kesetaraan, di mana kita mengekspresikan CTG X dan Sec X dalam hal payudara dan cosinus sebagai berikut:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Kami mengganti ekspresi ini di sisi kiri identitas dan menyederhanakan:

dosa x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

Dan kebenaran identitas sudah terbukti.

Jenis identitas trigonometri

Ada beberapa jenis identitas trigonometri. Selanjutnya kita akan menjelaskan secara singkat yang utama:

- Identitas trigonometri fundamental

Kami membedakan dua jenis identitas mendasar:

I) Mereka yang diekspresikan melalui alasan dasar, kosinus dan garis singgung:

• Sec x = 1 /cos x
• Hancurkan x / 1 / sin x
• CTG x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) Mereka yang berasal dari paritas. Kita tahu melalui grafiknya bahwa Sen X adalah fungsi yang aneh, yang berarti bahwa:

Dapat melayani Anda: 60 pembagi

sin (-x) = - sin x

Karena itu, cos x adalah pasangan, oleh karena itu:

cos (-x) = cos x

Jadi:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Demikian pula:

• cotg (-x) = -ctg x
• sec (-x) = dtk x
• bahaya (-x) = - bahaya x

- Identitas Pythagoras

Mereka adalah yang diperoleh dari penerapan teorema Pythagoras ke segitiga persegi panjang kucing A dan B dan hypotenusa C. Mari kita lihat:

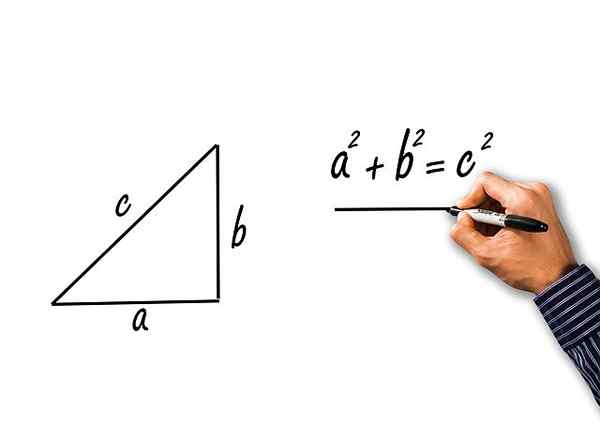Gambar 2.- Dari teorema Pythagoras, tiga identitas trigonometri Pythagoras diperoleh. Sumber: Pixabay.

Teorema Pythagoras menyatakan bahwa:

C² = a² + B²

Membagi segalanya antara C²:

C² / C² = (a² / C²) + (B² / C²)

Istilah di sebelah kiri adalah 1 dan mengingat bahwa sinus dan kosinus sudut akut α didefinisikan sebagai:

sin α = a/c

cos α = b/c

Hasil:

1 = (sin α)² + (cos α)²

Identitas ini dikenal sebagai Identitas mendasar.

Prosedur ini dapat dilakukan dengan membagi antara² dan B², yang memunculkan dua identitas lagi:

Detik² α = 1 + TG² α

har² α = 1 + CTG² α

- Rumus untuk kosinus dan payudara jumlah/pengurangan sudut

Identitas trigonometri utama untuk kosinus, payudara dan garis singgung dari jumlah dan pengurangan adalah sebagai berikut:

Demonstrasi Sen (α + β) dan COS (α + β)

Identitas ini dapat ditunjukkan secara geometris atau juga melalui rumus Euler:

Dan^Iα = cos α + i sin α

Mari kita lihat apa yang terjadi pada formula saat mengganti jumlah dua sudut α dan β:

Dan^{I (α +β)} = cos (α + β) + i sin (α + β)

Ekspresi ini kompleks, bagian sebenarnya adalah cos (α + β) dan bagian imajinernya adalah i sin (α + β). Kami menjaga hasil ini untuk menggunakannya nanti dan fokus pada pengembangan bagian eksponensial:

Dan^{I (α +β)} = e^Iα ⋅ e^Iβ = (cos α + i sin α) . (cos β + i sin β) =

Dapat melayani Anda: prisma heksagonal

= cos α⋅cos β + cos α⋅i sen β + i⋅sen α cos β - sen α⋅sen β

Bagian nyata dari ungkapan ini adalah yang tidak dikalikan dengan unit imajiner "i":

cos α⋅cos β - sen α. Sen β

Bagian imajiner karena itu adalah:

I (cos α⋅sen β + sen α⋅cos β)

Agar dua ekspresi kompleks sama, bagian nyata dari satu harus sama dengan bagian nyata dari yang lain. Hal yang sama berlaku untuk bagian imajiner.

Kami mengambil hasil yang disimpan dan membandingkannya dengan ini:

cos α. cos β - sen α. sin β = cos (α + β)

I (cos α⋅sen β + sen α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. Sin β + sen α⋅cos β)

- Rumus untuk sudut ganda

Dalam rumus sebelumnya kami mengambil β = α dan mengembangkan:

sin (α + α) = sen 2 α = sen α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cos² α - sen ² α

Tg (α + α) = TG 2 α = [TG α + TG α] / [1- TG α⋅TG α] = 2TG α / 1- TG² α

Jika dalam ekspresi kedua cos diganti² α = 1 - sen² α diperoleh:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Formula setengah -jarak

Dalam ungkapan terakhir ini kami mengganti α dengan α/2, berikut ini tetap:

cos α = 2 cos ²(α/2) -1

Membersihkan:

Latihan terpecahkan

- Latihan 1

Menunjukkan bahwa:

Larutan

Kita akan bekerja secara aljabar istilah yang tersisa sehingga terlihat seperti benar. Seperti dalam istilah yang benar muncul Sen X, langkah pertama adalah mengekspresikan COS²X Dalam hal sen x sehingga semuanya dalam hal alasan trigonometri yang sama:

Itu dapat melayani Anda: fraksi setara dengan 3/5 (solusi dan penjelasan)

Kemudian 1 - Sen adalah faktor² x Untuk menjadi perbedaan kotak sempurna. Untuk melakukan ini, itu jelas dari identitas mendasar:

cos²X = 1 - sen² X

1 - sen² x = (1- sin x) (1+senx)

Dan faktorisasi dalam ekspresi asli diganti:

Istilah (1- senx) disederhanakan dan kesetaraan tetap:

1 + sen x = 1 + senx

- Latihan 2

Selesaikan persamaan trigonometri berikut dan berikan solusi untuk nilai antara 0 dan 360º:

TG X + SEC² x = 3

Larutan

Dalam istilah kiri ada dua alasan trigonometri, oleh karena itu Anda harus mengurangi segalanya menjadi satu, untuk dapat membersihkan yang tidak diketahui. Istilah Sec² X diekspresikan melalui salah satu identitas Pythagoras:

Detik² α = 1 + TG² α

Dengan mengganti persamaan:

TG X + 1 + TG² x = 3

Mengatur ulang istilah:

Tg² x + tg x + 1 = 3

Persamaan ini diselesaikan dengan mengubah variabel:

tg x = u

atau² + U + 1 - 3 = 0 → u² + U - 2 = 0

Persamaan tingkat kedua ini mudah diselesaikan dengan faktorisasi:

(U +2) (u-1) = 0

Oleh karena itu u₁ = -2 dan u₂ = 1, setara dengan:

TG x₁ = -2

TG x₂ = 1

Akhirnya:

X₁ = arctg (-2) = 296.6

X₂  = arctg (1) = 45º

Referensi

1. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
2. Figuera, J. 1999. Matematika. 1st. Diversifikasi. Edisi Collegiate Bolivarian.
3. Hoffman, J. Pemilihan masalah matematika. Volume 4.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Wikipedia. Identitas dan formula trigonometri. Pulih dari: is.Wikipedia.org.
6. Zapata, f. 4 cara untuk menyelesaikan persamaan tingkat kedua. Pulih dari: francesphysics.Blogspot.com.
7. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.